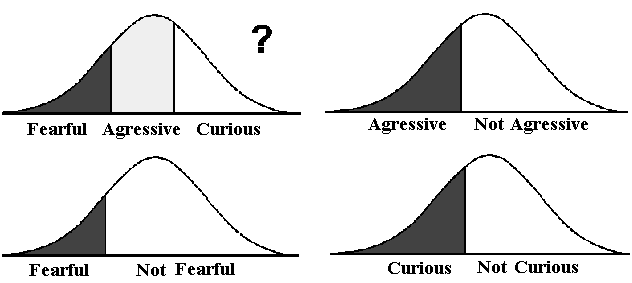
| Figura 8.2. Las tres características agresivas, curiosos y temerosos, no puede interpretarse en una escala lineal. Cada uno de ellos tiene que tener su propio escala presente o no. |
 |
Desde el capítulo 1 se repite que un rasgo umbral se hereda como un rasgo cuantitativo, que contiene la característica que se presenta como un rasgo presente o no. Como ejemplo son la mastitis en vacas lecheras, o una anomalía en el corazón de un cachorro recién nacido.
Considerando que el número de brotes de mastitis en la vaca puede ser considerado como un rasgo semi cuantitativo, en particular, visto en un segundo plano de toda una vida con muchas lactancias. En cuanto al número de casos de mastitis, no hay duda, que una relación lineal se producen entre el número de casos y de los animales con resistencia a la enfermedad.
En otros casos es más difícil imaginar una escala lineal. Por ejemplo en el llamado "prueba de palo y pluma" para el visón, diseñado para probar sus patrones de reacción. Los posibles resultados de la prueba son agresivos, curiosos o temerosos, todos los cuales puede verse en la misma prueba. Es importante para poner las tres clases en la misma escala lineal y en caso afirmativo ¿cómo?
Para obtener un resultado significativo de la prueba es necesario usar los tres resultados independientemente, ya sea escalas que debe ser utilizado. 1) agresivo o no agresivo, 2) miedo o no miedo, y 3) curioso o no curioso, ver Figura 8.2.
| Figura 8.2. Las tres características agresivas, curiosos y temerosos, no puede interpretarse en una escala lineal. Cada uno de ellos tiene que tener su propio escala presente o no. |
 |
Un ejemplo de la utilización de una escala semilineal: La displasia de cadera (HD) en perros Pastores alemanes
de Andresen et al. Índice HD: Bedømmelsen bør bruges
efter hensigten. Hunden dec.1994.
Figura 8.3 muestra un ejemplo, que se trata de la displasia de la cadera (HD) en
Pastores alemán. Éstos son los datos de una población de 1406
radiografía de perros. Todas las caderas de los perros fueron evaluados en una escala de E2, E1 a A2, A1,
10 clases en total, como se muestra en la figura. Los E2 perros tienen un grado muy alto de
HD, y los perros A1 tienen caderas perfectas. Perros de B2 y a continuación
a la izquierda
tienen un aumento grado de HD.
Como se puede ver en Figura 8.2, la escala no es lineal cuando está equipado de los datos
en una distribución normal. En el cálculo del índice de alta definición, la clase media
se ha utilizado en lugar de una escala de diez pasos completamente lineal. La media de clase ha sido
determina da a partir de la distribución normal con
un valor medio de 0 y una desviación estándar
de 1.
La estimación del valor de cría (índice HD) de un individuo sobre la base
de 15 crías se muestra a continuación. La descendencia tuvo la puntuación
4 A2, 9 B1, 1 B2 y 1 D1 con un
valor promedio de 0,2933. Para reescalar los valores de cría, 100 se añade y la desviación se multiplica por 100, Los animales con un índice de
más de 100 son mejores
que la media. El cálculo real del valor genético se realiza de acuerdo a las fórmulas dadas en
la sección 7.2 El cálculo del índice HD está muy por encima de la media, que también puede
deducirse del hecho de que el macho sólo tiene dos hijos con B2 o por debajo.
El cálculo del índice HD se puede estandarizar variar
entre 50 y 150, El índice actual es "estandarizadas" al azar con el factor de 100,
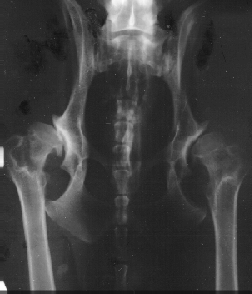
Figura 8.4 muestra los rayos X de las mejores caderas, A1, y lo peor, E2.
Las fotos han sido tomadas en el
Röntgen-Klinikken.
HD puntuación, A1
Desde abril de 2000 El Kennel Club Danés ha alterado la escala de evaluación de alta definición,
ahora es una escala de cinco niveles que sólo contiene los grados A, B, C, D y E, este
nueva escala se ha adaptado a nivel internacional.
En el ejemplo presente, la índice HD se puede calcular con la nueva escala
con los valores
1,02, -,02, -,90, -1,47 y -2,16. Comparación de la ocurrencia de enfermedades umbrales y de las
mendelianas.
En el capítulo 5 se dio una descripción detallada de la segregación de
Mendel de
las enfermedades en las familias. Todas estas formas de ocurrencia dentro
de las familias. Lo mismo ocurre para una enfermedad umbral. Estimación de la heredabilidad de los rasgos de umbral. En el capítulo 6 métodos
para estimar la heredabilidad para
un rasgo cuantitativo normal distribuido
fue dado. La
heredabilidad se puede estimar para una enfermedad umbral cuando se conoce
la frecuencia de la población, así como la frecuencia en la descendencia
de los animales afectados o de
los familiares de los animales afectados.
Una estadística del tipo actual también puede considerarse como una
investigación epidemiológica,
el factor de riesgo es la relación de un individuo afectado. El
riesgo relativo de contraer la enfermedad es 4 veces mayor en la descendencia de
los dos padres afectados que en un individuo elegido al azar en la población
como se muestra
en Figura 8.5.
Figura 8.3
Una escala en parte lineal se utiliza para graduar la gravedad de la HD. El número en
cada clase está adaptado
a la distribución normal.
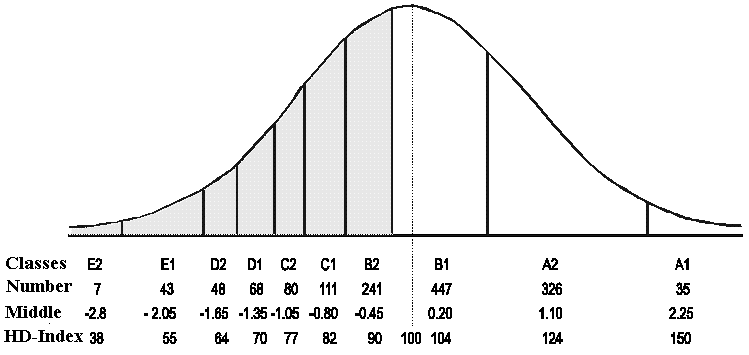

Figura 8.4
izquierda y E2 derecha.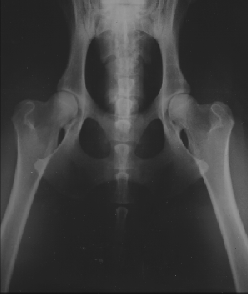
Para las enfermedades con una frecuencia población baja no es posible discernir
entre una enfermedad mendeliana y un umbral. En ambos casos, la frecuencia de
la enfermedad es mucho mayor en individuos que están estrechamente relacionados con una enferma, que la frecuencia en la población general.
La diferenciación entre las dos formas de herencia sólo puede hacerse por
medio de la prueba de apareamiento. En el caso de las enfermedades mendeliana heredado
las proporciones exacta de segregación se pueden predecir.
Este no es el caso de los rasgos de umbral.
Figura 8.5
Cálculo de la heredabilidad sobre la base de
frecuencia de la enfermedad en parientes de los animales afectados.
En este
caso los padres afectados. 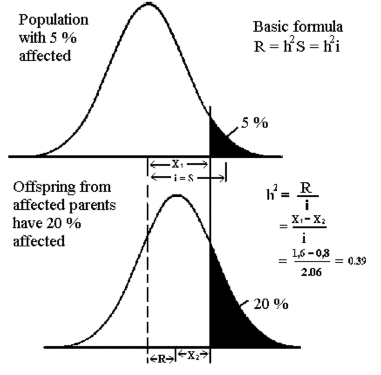
Figura 8.5 muestra un ejemplo de la estimación de heredabilidad en forma gráfica.
La frecuencia en la población es 5% y la frecuencia en la descendencia de
los animales afectados es de 20%. La situación puede considerarse como un
experimento de selección, donde
sólo los animales afectados son seleccionados para la reproducción. Ahora, la fórmula
simple para el delta G
o la respuesta a la selección, R = S*h2 puede ser utilizado. El rasgo umbral es
medido en una distribución normal estandarizada con S = i. La respuesta R es la diferencia entre la
X1 y X2.
(Se puede leer en una tabla de
la distribución normal.) La intensidad de selección (i) es también en la tabla de
i. La heredabilidad en este caso se estima en 0,39.
Si se conoce la frecuencia de los animales afectados, como por ejemplo en
primer grado
de parientes (padre, madre o hermanos completos), los cálculos se realizan como se muestra en el ejemplo,
pero luego h2/2 se calcula como el R/i.
En los datos de los parientes de segundo grado, como por ejemplo, medios hermanos, se estima que
resultado es h2/4.
Un applet para el cálculo de la heredabilidad
de los rasgos de umbral
haga clic aquí