7.2 Estimación de los valores de cría usando el modelo de animal
Los cálculos se basan en parte de la matriz general que ha sido producido
de Bryan Lewis con su applet matriz general.
La parte general incluyen, por ejemplo matriz multiplicatión como A = b*c o A = b*c', que puede ser utilizado junto
con los cálculos del modelo de animal.
El applet se puede manejar cálculo de la consanguinidad y relación,
la matriz inversa y la estimación de los valores de cría del modelo de animal. Enlace ejemplo
... Input aera .... ....Output area ....
La estimación de las valores de cría del modelo de animal, comando an=:animalm(a), se puede corregir para
cualquier número de variables de clase o variables continuas en cualquier combinación.
Para las variables de clase la primera clase es excluida por no haber
un grado de libertad porque el valor medio siempre se calcula.
El cero es considerado como valor perdido, si el cero es una
parte del conjunto de observaciones una constante se debe ser añadida.
Las primeras 3 columnas en el conjunto de datos deberá contener animal, padre y madre - todas las demás columnas
se pueden utilizar libremente
Los parámetros de la primera línea de datos especifica - refiriéndose al ejemplo seguido y en general
1. 1 especifica (sigmaE/sigmaA)2 en este caso 1 es igual a h2 = 0,50
2. 0 impresión de las soluciones
1 impresión de las soluciones y la precisión cuadrada, para un número pequeño de datos (pc tiempo problemas)
2 impresión de la triangualrization incluido la variable dependiente - la última línea las soluciones
3 impresión de la entrada matriz reorganizado con las clases de cero a n-1 y la variable dependiente como la final.
4 impresión de las ecuaciones incluido la variable dependiente.
3. 0 no incluyendo la consanguinidad
1 modelo incluyendo la consanguinidad - para menor número de datos (más redondeos y problemas de PC tiempo)
4.- 0 excluir el rasgo del análisis
1 especificar una variable continua, el último es el rasgo dependiente
-1 especificar la variable dependiente, si no es el último rasgo - que luego se intercambian con la última variable
2 especificar una variable de clase (factor fijo)
3 especificar una variable de clase donde se usan todos las clases (no puede ser resolvado)
Modelo de animal soluciones se obtiene con la inserción del comando an=:animalm(a) en la ventana de entrada.
Ejemplo de estimación de valores de cría ded modelo de animal de 8 animales,
la lista de entrada contiene:
Animal padre, madre, donde 0 significa desconocido, un factor fijo,
dos variables continuas,
y el tamaño de la camada.
- excepto la primera línea que se especifican los parámetros que se
explican por encima
Ponga los datos
en el área de entrada,
seguido de un retorno
a=
1 0 0 2 1 1 1
1 0 0 3 2 0 10
2 0 0 2 3 1 9
3 0 0 1 4 0 8
4 0 0 2 1 1 7
5 1 2 1 5 1 9
6 1 2 1 6 0 10
7 3 4 2 4 1 8
8 5 6 3 6 1 11
| Diagram genealogical
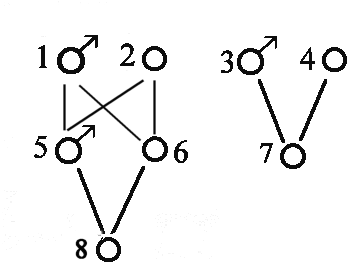 |
Resultando en los siguientes
en el output área
a =
1 0 0 2 1 1 1
1 0 0 3 2 0 10
2 0 0 2 3 1 9
3 0 0 1 4 0 8
4 0 0 2 1 1 7
5 1 2 1 5 1 9
6 1 2 1 6 0 10
7 3 4 2 4 1 8
8 5 6 3 6 1 11
|
Seguido de an=:animalm(a)
y presionar de retorno
Animal model solutions
an =
1.0000 0.1955
2.0000 0.4287
3.0000 -0.3799
4.0000 -0.2443
5.0000 0.3420
6.0000 0.3582
7.0000 -0.4206
8.0000 0.2903
0.0000 6.9749 el valor medio
2.0000 0.5183 clase, no hay un grado de libertad para la clase 1
3.0000 1.8716 clase
0.0000 0.4191 regresión 1
0.0000 -0.5322 regresión 2
|
El primer ejemplo en la teoría de Poul Jensen se refiera a la tasa de crecimiento en cerdos jóvenes aquí
los resueltos son diferentes como el año en la clase se da para todos los animales de la siguiente manera.
Pero el sistema aquí anulará el primer año y luego se convierte en una regresión dando 4,3883 gramo extra
del segundo año.
La heredabilidad se establece en 0,33.
a=
2 0 0 2 1
1 0 0 0 0
2 0 0 1 225
3 0 0 1 220
4 0 0 1 255
5 1 3 2 250
6 1 3 2 198
7 2 4 2 245
8 2 4 2 260
9 2 4 2 235
|
Diagram genealogical
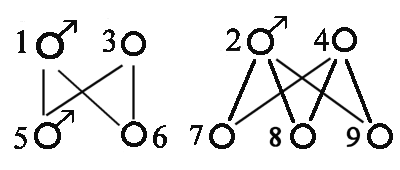 |
Animal model solutions
animal estimate
an =
1.0000 -3.1844
2.0000 -0.3009
3.0000 -6.2135
4.0000 9.6990
5.0000 -1.0912
6.0000 -11.4912
7.0000 5.4271
8.0000 8.4271
9.0000 3.4271
0.0000 232.2718
0.0000 4.3883
|
En el caso de algunos de los padres son consanguinas las estimaciones no será el mismo. En las siguientes
soluciones de un pequeño ejemplo se hacen con (parámetro 3 a 1). Un ejemplo 2.1 de RA. Mrode
'linear models for estimating breeding values, CABI Publishing'. La heredabilidad se establece en 0,33.
a=
2 0 1 1
1 0 0 15
2 0 0 19
3 1 2 7
4 1 0 13
5 4 3 22
6 5 2 10
|
Diagram genealogical
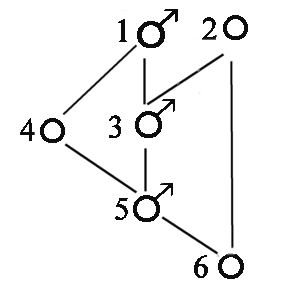 |
Animal model solutions
accounting for innbreeding
an =
1.0000 -0.3665
2.0000 0.1689
3.0000 -1.0983
4.0000 0.1131
5.0000 0.7070
6.0000 -0.4987
0.0000 14.4957
|
Animal model solutions
no accounting for innbreeding
an =
1.0000 -0.3699
2.0000 0.1725
3.0000 -1.0988
4.0000 0.1110
5.0000 0.7084
6.0000 -0.5484
0.0000 14.5041
|
La estimación de la precisión cuadrado para la estimación, ejemplo 3.1 de RA Mrode.
La heredabilidad se establece en 0,33.
a=
2 1 0 2 1
1 0 0 0 0
2 0 0 0 0
3 0 0 0 0
4 1 0 1 4.5
5 3 2 2 2.9
6 1 2 2 3.9
7 4 5 1 3.5
8 3 6 1 5.0
|
Genealogical diagram
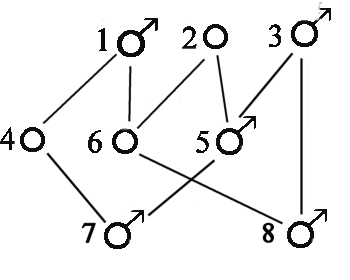 |
Animal model solutions
with its squared accuracy
an =
1.0000 0.0984 0.0578
2.0000 -0.0187 0.0158
3.0000 -0.0410 0.0870
4.0000 -0.0086 0.1446
5.0000 -0.1857 0.1437
6.0000 0.1768 0.1154
7.0000 -0.2494 0.1162
8.0000 0.1826 0.1552
0.0000 4.3585 0.
0.0000 -0.9540 0. |
Soluciones de un ejemplo más grande, numeración de los animales está libre,
siempre y cuando los animales más antiguos son los primeros. La heredabilidad se establece en 0,33.
El sexo 2 tiene 5,6002 unidades menos del sexo 1 (último línea).
animal sire dam y sex trait2
a=
2 0 0 -1 1 2
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
7 0 0 93 2 2
8 1 2 78 1 2
9 1 2 63 1 3
10 1 3 91 1 3
11 1 3 70 2 3
12 1 3 100 2 2
13 1 4 102 1 4
14 1 5 119 1 5
15 1 5 121 2 4
16 1 6 93 2 6
17 1 6 81 2 4
18 1 6 82 2 3
19 14 17 78 2 2
20 14 17 88 1 5
21 14 17 85 2 6
22 14 7 91 2 5
23 14 7 113 1 7
24 14 7 118 2 5
25 14 15 91 2 4
26 14 15 83 2 2
27 14 15 102 1 4
128 14 12 87 2 5
29 14 12 83 1 3
30 14 12 86 1 3
31 14 16 106 2 4
32 14 16 90 1 5
33 14 16 57 2 3
34 23 25 82 1 2
35 23 25 84 1 1
36 23 25 77 2 3
37 23 22 83 2 2
38 23 128 95 1 5
39 23 128 68 2 4
40 23 31 116 1 6
41 23 31 112 1 7
42 23 31 88 2 5
43 23 24 121 1 4
44 23 24 98 1 4
45 23 24 86 1 4
|
Animal model solutions
The first variable contains numbers
of animal (mean) classes and regressions
and the second the estimate
an =
1.0000 -1.4325
2.0000 -4.4927
3.0000 3.1002
4.0000 0.4142
5.0000 2.9162
6.0000 -3.3706
7.0000 2.8651
8.0000 -4.7612
9.0000 -5.6569
10.0000 2.9802
11.0000 -0.0996
12.0000 2.7212
13.0000 -0.0949
14.0000 -0.4850
15.0000 4.8850
16.0000 -3.7721
17.0000 -6.5152
18.0000 -0.2880
19.0000 -4.0711
20.0000 -5.4854
21.0000 -5.5097
22.0000 -0.0535
23.0000 -1.6506
24.0000 5.2497
25.0000 0.6864
26.0000 1.4889
27.0000 2.0724
128.0000 -3.1481
29.0000 1.6076
30.0000 2.2076
31.0000 0.8187
32.0000 -3.9882
33.0000 -5.0696
34.0000 -1.9767
35.0000 -0.4821
36.0000 0.2475
37.0000 -0.9527
38.0000 -3.2048
39.0000 -7.2870
40.0000 2.0375
41.0000 -0.6642
42.0000 -1.8980
43.0000 5.5520
44.0000 0.9520
45.0000 -1.4479
0.0000 90.0823
2.0000 5.4732
3.0000 -5.0481
4.0000 15.9558
5.0000 16.9446
6.0000 19.6661
7.0000 29.1753
0.0000 -5.6002
|
Volver a la teoría 3 de modelo de animal , en Inglés y de nuevo a la teoría
4 de modelo de animal , en Inglés;
que hayan sido producidos por el finado Poul Jensen.
or Volver al otro applets



