By selecting against the recessive the following table is obtained. Selection (s) against the recessive is relative compared to the dominant types. The proportion selected of a given genotype is given the symbol s, which do not reproduce in every generation. Therefore, the fitness is equal to 1-s.
Table formulating selection: --------- Genotype EE EE ee Total Frequency p2 2pq q2 = 1,00 Fitness 1 1 1-s Proportion p2 2pq q2(1-s) = 1-sq2 after selection ---------
After selection the gene frequency is calculated by the gene counting method. The new gene frequency q' is estimated as the heterozygotes plus 2 times the surviving recessive relative to 2 times the proportion of all surviving genes after selection, which is equal to 1-sq2.
q' = (2pq + 2*q2(1-s))/(2(1-sq2))
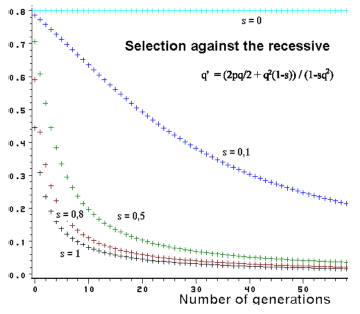
Figure 3.3. Effect of selection against the recessive and changes in
gene frequency through generations. At
a low gene frequency the changes are very slow.
 |
The frequency q' represents the genes which survive and therefore corresponds to the gene frequency in the next generation before selection. The formula can be applied repeatedly generation after generation. In the right side of the formula q' is calculated in the preceding generation and so forth.
Figure 3.3 shows such an application. By strong selection (s=1) the gene frequencies change very rapidly at high gene frequencies. If the gene frequency in contrast is low, the selection will hardly affect the frequency, the population has parked the gene in waiting position so to speak. This causes some problems if it concerns a recessive disease gene in an animal population. Selection can not really solve this problem. Therefore there is great interest in finding a DNA test method to diagnose the heterozygotic carrier. From Figure 3.3 it also becomes evident that by weak selection pressure the changes in the gene frequency are always very slow.
For s=1 the formula for gene frequency changes can be expanded to n generations, when q0 is the gene frequency in the initial population:
qn = q0/(1+n*q0)
From this formula n can be isolated and it can be calculated how many generations is needed to obtain a given change in the gene frequency q.
n = 1/qn - 1/q0
Example: When s=1 the gene frequency change from 0.01 to 0.005 would take
n = 1/0.005 - 1/0.01 = 200 - 100 = 100
It takes 100 generations to change the frequency of a lethal gene from 1 % to 5 per thousand.
For an applet, as seen below, for calculating gene frequency changes for different fitness combinations, click here The Calculations show that the gene frequency change from .5 to .42 after one generation of selection when the fitness of the recessive is equal to .5.

DNA test and culling of heterozygotic males
It takes a very long time to eliminate a recessive disease gene from a
population, when there
has only been selected against the recessive. In many
populations relatively fewer males than females exist. Therefore, it is often
enough to DNA test the males. As the males contribute to half of the
genes in the new generation, the gene frequency of the disease gene would
be halved in every
new generation, if only free males are used for breeding. At the
same time it is attained that no segregation of recessively affected
individuals will occur.
Example: The recessive inherited disease BLAD (Bovine Leukocyte
Adhesion
Deficiency) occurs in HF dairy breeds. In 1992 the gene frequency in the
Danish female population was about 15% of the BLAD gene. By systematically
'BLAD' DNA testing all new bulls the frequency in year 2000 is down to less
than 7%. By this procedure the frequency of the BLAD gene is halved in every new
generation.