When a smaller material is pointing at Mendelian segregation, there would often be alternative hypotheses, which cannot be excluded. The segregation can, as mentioned earlier, also be caused by simulated genetics (phenocopies) or threshold inheritance, where the segregation can resemble simple Mendelian inheritance. If a given hypothesis is to be accepted, test mating is in many cases simply waiting for more offspring to be born, in which the results are predictable. If the results deviate, a new hypothesis, which can be tested, has to be formulated.
How much data material is needed for a given test to give a final answer?
This is one of the important questions that have to be answered before the initiation of test mating.
Test mating of a bull, which is a suspected carrier, can be done by mating the bull with known affected cows, known carriers or the bull's own daughters. Taking these cases into consideration, how many normal offspring does the bull have to produce before he can be declared unaffected? The probability that one normal offspring is born in the three cases is respectively 1/2, 3/4 and 7/8. By applicating the multiplication rule for probabilities in mating with known carriers, the probability of getting one normal offspring is (3/4)n. By means of this formula and a limit of significance of 0.05, 0.01 and 0.001 n can be determined to meet the classic probability criteria.
Number of normal offspring (n) which is needed to exclude a bull as carrier
Exclusion of bull Probability Formula as carrier by test ------------------------------ mating with 0,05 0,01 0.001 (x)n less than Knowingly recessive 5 7 10 x=1/2 Known carrier 11 16 24 x=3/4 Own daughters 23 35 52 x=7/8
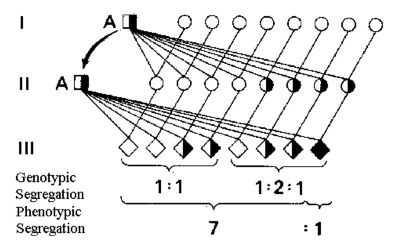
Figure 5.6
Theoretical segregation of recessive genes in test mating with own daughters.
 |
For normal offspring of a heterozygotic individual by father/daughters mating the probability is 7/8, as can be derived from Figure 5.6. The number of offspring needed to declare the father non-carrier on the 5% level is (7/8)n = 0,05 corresponding to n*ln(7/8) = ln(0,05), which rounded is n=23.
Mating with own daughters also has the advantage that the bull is tested as carrier of all possible recessive genes, not only the one he is suspected of having.
Chi-square tests
By testing for segregation ratios for known mating a Chi-square test can be utilized. The test for mating with known carriers resembles the test for H-W equilibrium, but here the expected numbers are in the ratios 1:2:1 for co-dominant and 3:1 for dominant cases. The expected numbers are calculated by multiplying the expected frequencies (ratios) with N, as shown in the table below.
Segregation by test mating of Aa x Aa, codominant inheritance.
--------- Genotype AA Aa aa Total Numbers, obs 30 51 39 = 120 = N Frequency, exp 1/4 1/2 1/4 = 1,00 Numbers, exp 30 60 30 = 120 Deviation 0 -9 9 Chi-squared 0 1.35 2.70 = 4.05 ----------
Df = 3-1 = 2, since the material only supplies the parameter N to the calculation of expected numbers. The Chi-square value is less than the H0 test value of 5.99, which means that there is no statistical significant deviation from a 1:2:1 segregating on the 5% level.
Segregation by test mating of Aa x Aa, dominant inheritance
--------- Genotype AA+ Aa aa Total Numbers, obs 81 39 = 120 = N Frequency, exp 3/4 1/4 = 1,00 Numbers, exp 90 30 = 120 Deviation -9 9 Chi-squared 1.00 2.70 = 3.70 ----------
Df = 2-1 = 1, since the material only supplies the parameter N to the calculation of expected numbers. The Chi-square value is just below the H0 test value of 3.84, which means that there is no statistical significant deviation from a 3:1 segregation on the 5% level.
Applet for calculating the Chi-square for Mendelian segregation by test mating, is found here.