Løsninger, Lektion 2, link opgaver
1 Genfrekvensen for Z og z i blodtypesystemet bliver efter gentælle metoden. Race Genfrekvens p(Z) q(z) RDM 0,14 0,86 SDM 0,08 0,92 Jersey 0,46 0,54 De forventede H-W ligevægts genotypefrekvenser hos afkom. Race p2 2pq q2 Z Zz z RDM 0,02 0,24 0,74 SDM 0,01 0,15 0,84 Jersey 0,21 0,50 0,29 2 I en tilfældig sammenparret population svarer frekvensen af homozygotisk recessive individer (aa) til q2 = 0,01, hvilket giver q=0,1 og p=0,9. a) Frekvensen af heterozygotiske individer (Aa) = 2pq = 0,18. b) De dominante fænotyper består af AA og Aa, hvoraf Aa individer udgør 2pq/(p2 + 2pq) = 0,182 3 Genfrekvensen af sygdomsgenet er 0,005. a) Sandsynligheden for i populationen at finde raske forældre (A-) med afficeret afkom er (2pq)2*(1/4) = 2*10-5 b) Sandsynligheden for i populationen at finde forældre, hvoraf mindst Ún er syg med afficeret afkom 1) den ene forælder syg 2*(2pq)*q2*(1/2). 2) begge forældre syge q2*q2 =q4. sum 2*10-7 c) Forhold mellem de under punkt a) og punkt b) fundne sandsynlig- heder (2pq)2*(1/4)/[2*(2pq)*q2*(1/2) + q4] = p2/(1 -p2) = 99 Kommentarer til det fundne resultat: De syge individer er som regel afkom efter normale forældre, derfor vil selektion mod den recessive kun langsomt fjerne sygdommen. 4 Genfrekvensen findes ved hjælp af kvadratrods-metoden q(r) = 0,6. a) Gravhunde der må antages at være anlægsbærere = 2pq*N = 48. b) Sandsynligheden for at den første hvalp bliver korthåret efter sammenparring af to tilfældigt valgte ruhårede hunde (5/7)2*(1/4) = 0,13. 5 Ved en kønsbunden recessiv egenskab er genfrekvensen lig med fænotype- frekvensen hos hankøn a) Hæmophili blandt mænd q(h) = 1/10000 = 10-4. b) Hæmophili blandt kvinder q2 = (1/10000)2 = 10-8. Heraf ses, at mænd får hæmophili med langt større hyppighed end kvinder. 6 Moderen har blodtype BB eller B0 og faderen blodtype AA eller A0, men da de har et barn med blodtype 0, er deres blodtyper B0 og A0. Deres eventuelle fremtidige børn kan få blodtyperne A0, B0, AB eller 0. 7 a) Frekvensen af genet for henholdsvis rød og sort farve beregnes efter gentælle metoden. p(rød) = (13655+678/2)/14345 = 0,97553 q(sort)= (12 +678/2)/14345 = 0,02447 b) Undersøg ved en Chi-i-anden test, om de observerede antal stemmer overens med de forventede under Hardy-Weinberg ligevægt. Genotyper sorte intermediære røde Observeret 12 678 13655 Forventet 8,58 684.82 13651,58 Chi-i-anden 1,36 0,07 0,00 = 1,43 Det forventede antal er beregnet på grundlag af de estimerede parametre p, q og N. q er en funktion af p, derfor er der anvendt to frie parametre til beregning af forventet antal. Antal frihedsgrader er derfor lig med 3 - 2 = 1. Der er ikke statistisk signifikant afvigelse fra H-W ligevægt. Signifikansgrænse med df=1 er 3,84. 8 a) Genotyperne er angivet ved deres allelnumre, og de forventede frekvenser er anført for hvert locus. Genotyper locus A locus B 1/1 0,01 0,04 1/2 0,06 0,12 1/3 0,12 0,20 2/2 0,09 0,09 2/3 0,36 0,30 3/3 0,36 0,25 b) Forventede frekvens i populationen af genotypen A1A2B1B2 er 0,06 * 0,12 og af genotypen A3A3B3B3 er 0.36 * 0,25 En hanhund med genotypen A1A2B1B2 parres med et antal tæver med genotypen A3A3B3B3. c) Forventede genotyper blandt afkom efter nævnte parringer når de to loci ikke er genetisk koblede og deres frekvens er følgende: A1A3B1B3 er 0,25 A1A3B2B3 er 0,25 A2A3B1B3 er 0,25 A2A3B2B3 er 0,25 d) Forventede genotyper blandt afkom efter nævnte parringer når de to loci er genetisk koblede (c=0,2) og deres frekvens er følgende: A1A3B1B3 er 0,40 A1A3B2B3 er 0,10 A2A3B1B3 er 0,10 A2A3B2B3 er 0,40 9 a. Haplotype NE : 0,3 Haplotype Ne : 0,1 Haplotype ne : 0,6 b. Frekvensen af grise som er modtagelige for ødemsyge stiger. Samtlige ne/ne grise fjernes, Frekvensen af disse er 0,6x0,6 = 0,36, dvs 36% af grisene fjerne ved denne selektion. Resten af grisene fordeler sig som følger: 9% NE/NE, 6% NE/Ne, 36% NE/ne, 1 % Ne/Ne, 12% Ne/ne Haplotypefrekvenserne bliver herefter: Haplotype NE : (2x9 + 6 + 36)/2x64 = 0,4688 Haplotype Ne : (6 + 2x1 + 12)/2x64 = 0,1563 Haplotype ne : (36 + 12)/2x64 = 0,375 Bemærk! Efter selektion vil der være 79,69% grise som er modtagelig for ødemsyge. Før selektion var tallet 51% c. Grise med haplotypen Ne skal selekteres. Dette kan gøres ved at selektere for grise med genotypen N/N e/e eller ved at bruge genotypning i grisefamilier med mindst 3 generationer, så koblingsfasen kan fastlægges og herved kan grise med Ne haplotypen identificeres. Over generationer vil koblingsuligevægten mellem N og E nærme sig nul og det vil blive lettere at identificere individer med den favorable haplotype. 10 a) Koblingsuligevægten D = f(AB) - pA*pB = 0,4 - 0,5*0,6 = 0,10 b) I hver generation reduceres D med 1-c. Generation 0 1 2 3 4 5 6 7 8 9 -------------------------------------------------- D 0,10 0,07 0,05 0,03 0,02 0,02 0,01 0,01 0,01 0,00 c) Genfrekvenserne er konstante gennem generationerne og ved koblingsligevægt er: f(AB) = pA*pB = 0,5*0,6 = 0,30. f(Ab) = pA*qb = 0,5*0,4 = 0,20. f(aB) = qa*pB = 0,5*0,6 = 0,30. f(ab) = qa*qb = 0,5*0,4 = 0,20. d) Hyppigheden af dobbelt-heterozygoter i udgangspopulationen er. 2(f(AB)*f(ab) + f(Ab)*f(aB)) = 2(0,4*0.3 + 0,1*0,2) = 0,28 Ved koblingsligevægt 2(f(AB)*f(ab) + f(Ab)*f(aB)) = 2(0,3*0.2 + 0,3*0,2) = 0,24
Løsninger, Lektion 3, link opgaver
1 a) p(A)=0,4944 og q(a)=0,5056
Populationen er i Hardy-Weinberg ligevægt, da Chi-i-anden er
mindre end 0,1. Signifikansgrænse med df=1 er 3,84.
b) Genfrekvenserne i næste generation med saa = 0,1 bliver:
q' = [(1/2)*0,500 + 0,256*(1-0,1)]/(1-0,256*0,1) =
eller [(1/2)* 225 + 115*(1-0,1)]/(450-115*0,1) = 0,4926
q2 = 0.4799
q3 = 0.4677
q4 = 0.4558
q5 = 0.4442
2 Inden for SDM elimineres rødbrogede kalve fuldstændigt fra hver ny
afkomsgeneration.
a) En halvering af genotypefrekvensen af ee svarer til, at genfre-
kvensen sænkes fra 0,2 (4 % røde kalve) til 0,1414
(2 % røde kalve)
n = 1/0,1414 - 1/0,2 = 2,07
b) n = 1/0,01414 - 1/0,02 = 20,7
c) Forholdet mellem svarene i b) og c) er at det tager 10 gange så
lang tid at halvere frekvensen af røde kalve, når genfrekvensen
er 10 gange lavere. Ved lav frekvens har selektion mod den
recessive ringe effekt.
3 s1 = 0,2 og s2 = 0,7
a) Genfrekvensen q(hat) ved ligevægt
= s1/(s1 + s2) = 0,2/(0,2 + 0,7) = 0,22
b) Genotypefrekvenserne ved ligevægt forud for selektion:
Genotyper A1A1 A1A2 A2A2
Frekvens 0,61 0,34 0,05
c) Genotype-proportionerne efter selektion.
Proportion 0,61*0,8 0,34 0,05*0,3 sum = 0,843
Relativ frekvens 0,58 0,40 0,02
4 s1 = 0,2 og s2 =0,9
a) Frekvensen, q(hat), af Hbs ved ligevægt er 0,2/(0,2+0,9) = 0,18
b) Frekvensen af nyfødte med seglcelleanæmi vil falde, da recessive
ved ligevægt er 0,182 = 0,0324 er mindre end de nuværende 0,05.
5 a) Frekvensen af sygdomsgenet p(C) = (10/2)/94.000 = 5,32*10-5
b) Fertiliteten af dværgene (Cc) 27/108 = 0,25
Fertiliteten af normale (cc) 582/457 = 1,27
Dværge relativt 0,20
c) Skøn for mutationsfrekvensen c til C.
my = p*s = 5,32*10-5*0,80 = 4,26*10-5
6 Variansen på genfrekvensen regnes som en binominalvarians over udfald,
2N = 80. Variansp = 0,6*0,4/80 svarende til en spredning på 0,0548.
Sikkerhedsgrænserne for p svarende til en sandsynlighed på 5% bliver
0,6 plus/minus 2*0,0548 svarende til at genfrekvensen i generation 1 vil
ligge mellem 0,49 og 0,71.
7 a) 1/Ne = (1/4)*(1/5 + 1/50) svarende til Ne = 18,18
dvs. 9 hanner + 9 hunner
b) Stigningen i indavlsgraden pr. generation i de to populationer
er delta F = 1/(2*18,18) = 2,75 %
Løsninger, Lektion 4, link opgaver
1 For at beregne indavlskoefficienten reducerer man diagrammet,
så kun de relevante individer er med. Da ingen af individerne
A, B, C og D har fælles aner, kan ingen gener nå frem til X
i dobbelt dosis. X er ikke indavlet, da dets forældre E og G
ikke er beslægtede.
2 De indavlede individer er C, D og E.
aAB = 1/2 og FC = aAB/2 = 1/4
da A er fælles ane for de to forældre.
aBC = 1/2 + 1/4 og FD = aBC/2 = 3/8
da A og B er fælles ane for de to forældre.
aCD = 1/2(1+1/4) + 1/4 + 1/8 og FE = aCD/2 = 1/2
da A, B og C er fælles ane for de to forældre og C er indavlet.
eller med tabularmetoden
Forældre - 1 - 1-2 3-2 3-4
Dyr nr. 1=A 2=B 3=C 4=D 5=E
-----------------------------
1 1 1/2 3/4 5/8 11/16
2 1/2 1 3/4 7/8 13/16
3 3/4 3/4 1+1/4 1 9/8
4 5/8 7/8 1 1+3/8 19/16
5 11/16 13/16 9/8 19/16 1+1/2
Og her kan blive udledt en formel for indavl baseret på indavlen i
to tidligere generationer
F5 = a34/2 = (a32+a33)/4 = (2F4 + 1 + F3)/4
3 a) Opstil et pilediagram for individet A.



Løsninger, Lektion 5, link opgaver
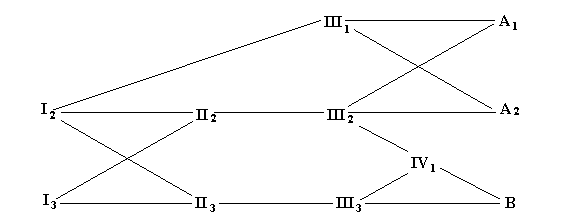
1 a) IV 1 og IV 4 er aa.
III 4 og III 8 er Aa da de får afficeret afkom.
II 2 og II 5 er Aa da II 1 og II 6 er AA.
b) Frekvensen af heterozygoter blandt fænotypisk normale
individer efter heterozygotiske forældre er
p(Aa | aa) = p(Aa)/(1-p(aa)) = (1/2)/(1 - (1/4)) = 2/3.
2 Kønsbunden dominant: Udelukket
Kønsbunden recessiv: Kan forekomme
Autosomal dominant: Udelukket
Autosomal recessiv: Kan forekomme
Kønsbunden recessiv er den mest sandsynlige arvegang, idet kun I 2
og II 2 skal være heterozygote, mens en autosomal recessiv arvegang
kræver at I 1, I 2, II 2 og III 1 er heterozygoter. Dominant arvegang
kan udelukkes, da ingen af forældrene i generation I er afficerede.
3 Kønsbunden dominant: Udelukket, idet II 7 skulle være afficeret.
Kønsbunden recessiv: Udelukket, idet III 3 og III 6 ikke kan være
være afficerede med mindre II 4 er det.
Autosomal dominant: Sandsynlig.
Autosomal recessiv: Kan ikke udelukkes.
En autosomal recessiv arvegang kræver at I 1, II 1 og II 4 er
heterozygoter, hvorimod autosomal dominant arvegang ikke stiller
nogen krav. Derfor må en autosomal dominant arvegang anses for
at være den mest sandsynlige.
4 Kønsbunden dominant: Arvegang er mulig.
Kønsbunden recessiv: Kan udelukkes, idet III 4 er almindelig.
Autosomal dominant: Arvegang er mulig.
Autosomal recessiv: Er ikke sandsynlig, idet I 2 og II 4 så skal være
heterozygote.
En han fra generation III med den nye pelskvalitet parres med
hunner med almindelig pels. Udspaltningen vil vise arvegangen.
5 En kønsbunden recessiv mutant vil først vise sig hos det hetero-
gametiske køn.
1) Høns høner (ZW kønskromosomer)
1) Kaniner hanner (XY kønskromosomer)
6 a) Det testes, om tyren er AA eller Aa, da den er mistænkt for at
være anlægsbærer.
Metode: Da den danske population udelukkende er AA, skal der
anvendes testparringer med egne døtre, som enten er AA (50%)
eller Aa (50%).
b) P(afficeret individ, dvs aa) = 1/8, P(normalt individ) = 7/8.
P(n normale individer) = (7/8)n, dvs. n findes ud fra
at (7/8)n = 0,05 ved en signifikansgrænse på 5%.
n = 23 stk afkom
c) Hvis der blandt de 23 stk afkom ikke er nogen med genotypen aa
(afficerede), kan det med 95% sikkerhed siges, at tyren ikke er
anlægsbærer (Aa) og derfor må være AA.
7 Der anvendes signifikansgrænse på 5%
1) P(n normale afkom) = (1/2)n = 0,05; n = 5 stk.
2) P(n normale afkom) = (3/4)n = 0,05; n = 11 stk.
3) P(n normale afkom) = (7/8)n = 0,05; n = 23 stk.
8 I spørgsmål b og c skal der tages hensyn til at I 2 og II 2 ikke er
af genotypen nn.
a) I 1 og II 1 er anlægsbærere for halotangenet n. Sandsynligheden
for at henholdsvis III 1, III 3 og III 5 er anlægsbærere er 2/3,
da de er normale og derfor kommer fra en fordeling på 1:2.
b) q = 0,2 og P(I 2 er Nn | den ikke er nn)
= 2*0,2*0,8/( 1-0,04) = 0,3333
c) P(III 6 er NN | den ikke er nn)
= ((1/2)*(1-0,3333/2))/(1-(1/2)*0,3333/2) = 0,455
9 Forventningen blandt afkom efter heterozygotiske forældre er 1:2:1,
derfor bliver Chi-i-anden beregningen med df=2
(39-30)2/30 + (51-60)2/60 + (30-30)2/30 = 4,05
Da Chi-i-anden værdien er mindre end tabelopslag for 5 % (5,99) er der
ikke statistisk signifikant afvigelse fra den forventede 1:2:1
udspaltning.
10 Ved en tilbagekrydsning med i alt 30 tilbagekrydsningsindivider kan
udspaltningsforholdet være følgende med tilsvarende Chi-i-anden
beregning.
Aa aa Chi-i-anden
30 0 30
. .
21 9 4,80
----------------------------------------------
20 10 3,33
. .
15 15 0 non-signifikant område
. .
10 20 3,33
----------------------------------------------
. .
0 30 30
Da df=1 kan hypotesen om recessiv nedarvning accepteres, med alle et
Chi-i-anden på mindre end 3,84 (5% signifikansgrænsen), dvs. en
udspaltning på mellem 10 til 20 eller op til det omvendte 20 til 10.
Løsningen på ligningen
chi-i-anden = (x-15)2/15 + ((30-x)-15)2/15 = (2/15)x2 + 4x2 + 30 = 3,84
er 20,37 og 9,63.
11 En kønsfordeling på to hanner og fire hunner i et kuld minkhvalpe
på seks stk. er binomialfordelt og har en sandsynlighed på
K6,2*(1/2)2*(1/2)4 = (6*5)/(2*1) * (1/64) = 0,23
12 Sandsynligheden for at en heterozygotisk ko får Ún kullet + tre hornede
kalve efter inseminering med heterozygotiske tyre er
K4,1*(3/4)1*(1/4)3 = 12/256 = 0,05
13 De mulige kombinationer af AA, Aa og aa i familier på tre søskende efter
parring mellem heterozygotiske forældre.
AA Aa aa
------------------
3
3
3
2 1
1 2
2 1
1 2
2 1
1 2
1 1 1
------------------
14 Der anvendes Chi-i-anden test, da der er tale om testparring
for udspaltningsforhold 3:1 med en hypotese om recessiv nedarvning.
Der er ialt 33 normale og 8 afficerede og Chi-i-anden bliver
(33-30,75)2/30,75 + (8-10,25)2/10,25 =0,66
Df=1, der er ikke statistisk signifikant afvigelse fra det forventede
ved en 3:1 udspaltning.
15 Undersøgelsen om udspaltningen af recessive i nærværende familie-
materiale hos kvæg om overensstemmelse med en 7:1 spaltning må gennem-
føres efter Singles metode, da familierne er fundet på grundlag af
mindst et afficeret afkom.
Total antal T=53
Antal afficerede A=13
Antal familier med 1 afficeret afkom A1=9
Antal familier med 2 afficerede afkom A2=2
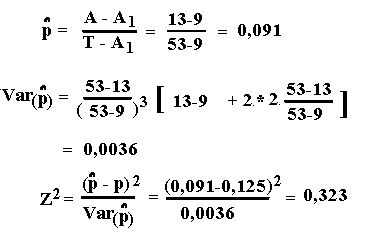
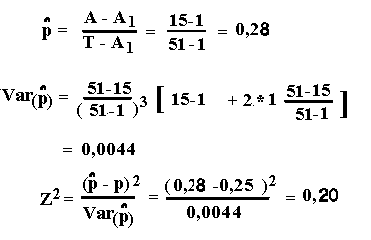
Løsninger, Lektion 6, link opgaver
1 p(Rd) og q(rd) er henholdsvis 0,7 og 0,3. Det gennemsnitlige riboflavinindhold pr. gram blomme er (summen af genotypefrekvens*værdi): 0,49*4,30 +0,42*2,50 + 0,09*0,40 = 3,19 2 a) Gennemsnitsfrekvensen for populationen er: 0,64 * 0,008 + 0,32*0,016 + 0,04 *0,020 = 0,0110 b) De tre genotypiske værdiers afvigelser fra populationsgennemsnittet AA 0,020 - 0,0110 = 0,0090 Aa 0,016 - 0,0110 = 0,0050 aa 0,008 - 0,0110 = -0,0030 c) Genotypeværdiernes (G) opdelt i en additiv del (A=avlsværdi) og en dominansafvigelse (D). Genotype G = A + D AA 0,0090 = 0,0116 + (-0,0026) AAA = 2(0,2*0,0090 + 0,8*0,0050) Aa 0,0050 = 0,0044 + 0,006 aa -0,0030 =-0,0028 + (-0,0002) Aaa = 2(0,2*0,0050 + 0,8*-0,0030) Avlsværdien bestemmes ved afkommets gennemsnit når en genotype parres tilfældigt i populationen. Dominansafvigelsen bestemmes som en rest. 3 Respons ved individuel selektion måles som: R = h2(SFædre + SMødre)/2 Indsættes i formel får man: (89,5-88,5) = h2((102-88,5) + (93-88,5))/2 og h2 = 0,11 4 h2 for smørfedtydelse beregnes p.g.a formel for selektionsrespons. R = h2(SFædre + SMødre)/2 R1 = h2(SFar + S1)/2 R2 = h2(SFar + S2)/2 ved subtraktion af de to formler får man: R1 - R2 = h2(S1 - S2)/2 266-259 = h2(295-227)/2, idet alle tal skal måles som afvigelse fra gennemsnit h2 = 0,21 5 Pilediagrammer over relationen mellem halvsøskende, mellem helsøskende og forældre-afkom.Den forventede fænotypiske korrelation mellem halvsøskende, mellem helsøskende og mellem forældre og afkom. Korrelationen halvsøskende r =(1/4)h2 helsøskende r =(1/2)h2 + c2 forældre-afkom r =(1/2)h2 6 På grundlag af et større observationssæt er der beregnet korrelation mellem beslægtede individer for vægt ved 6 uger hos grise. Resultaterne var følgende: Korrelationen halvsøskende r =(1/4)h2 = 0,05 helsøskende r =(1/2)h2 + c2 = 0,25 svarende til h2 halvsøskende = 0,20 c2 helsøskende = 0,15 h2 beregnet på helsøskendematerialet bliver 0,5, men da den beregnede på halvsøskendematerialet kun bliver 0,2, må der for helsøskende være en fælles miljø-komponent. Den fælles miljø-komponent for helsøskende kan tilskrives det maternelle miljø for kuldet. 7 På grundlag af et observationssæt er der beregnet korrelation og regression mellem beslægtede individer for højde hos veterinær- studerende. Resultaterne var følgende: Korrelationen mor-afkom r =(1/2)h2 = 0,45 far-afkom r =(1/2)h2 = 0,20 Regression afkom-gns. forældre b = h2 = 0,65 Korrelationerne svarer til h2 mor-afkom = 0,90 h2 far-afkom = 0,40 h2 beregnet på mor-afkom bliver meget høj, 0,90, i forhold til den beregnede på far-afkom, der kun bliver 0,40. Det kan tyde på at der er en fælles miljø-komponent for mor og afkom. Den lave værdi på far- afkom kan evt. tilskrives ukorrekt faderskab. Regression afkom på gns. forældre har været meget konstante gennem tiderne siden de første beregninger blev gennemført for mere end 100 år siden.
Løsninger, Lektion 7, link opgaver
1 Der anvendes formel for avlsværdiindeksets kvadrede sikkerhed.
n*h2*a'2/(1 + (n-1)(a*h2 +c2))
a'=1/2 a= - for moderens præstation rAI = 0,25
a'=1/4 a=1/4 for 50 halvsøskendes præstation rAI = 0,44
a'=1/2 a=1/4 for 20 stk. halvsøskende-afkom rAI = 0,76
Den største sikkerhed fås ved at måle 20 stk. halvsøskende-afkom.
2 Der anvendes formler fra kompendium for avlsværdi og sikkerhed.
1) egen ydelse 1. laktation, a'=1 a=-
4500 + [(1*0,25*1)/(1+0)]*(5000-4500) = 4625 kg; rAI = 0,50
2) gns. af egen ydelse i tre laktationer, a'=1 a=1
4500 + [(3*0,25*1)/(1+2(,25+,05))]*(4700-4500) = 4594 kg; rAI = 0,68
3) gns. af moderens ydelse i tre laktationer, a'=1/2 a=1
4500 + [(3*0,25*,5)/(1+2(,25+,05))]*(5000-4500) = 4617 kg; rAI = 0,34
4) gns. af 100 paternelle halvsøskende, a'=1/4 a=1/4
4500 + [(100*0,25*,25)/(1+99*,25*,25)]*(4600-4500) = 4587 kg; rAI=0,47
5) både 3) og 4), se formel afsnit 7.4
(på basis af forældres avlsværdi og sikkerhed).
(4617 + 4587)/2 = 4602 kg;
rAI = kvadratrod[(0,342+0,472)/4] = 0,29
Avlsværdiindekset for egenydelse i 3 laktationer er beregnet med størst
sikkerhed.
3 Egenskaben behandles som en tærskelegenskab med værdierne 0 og 1.
a) Populationsgennemsnittet for tærskelegenskaben OCD hos svenske
sportsheste er 0,7 og gennemsnittet for de 3 afkomsgrupper
er A 0,5, B 0,75 og C 0,80
b) De tre hingstes avlsværdiestimat vurderet på halvsøskende-afkom,
a'=1/2 a=1/4
Hingsten A har 40 stk. afkom, af hvilke 20 er OCD fri.
0,7 + [(40*0,20*,5)/(1+39(,20*,25))]*(0,5-0,7) = 0,43
Hingsten B har 60 stk. afkom, af hvilke 45 er OCD fri.
0,7 + [(60*0,20*,5)/(1+59(,20*,25))]*(0,75-0,7) = 0,78
Hingsten C har 20 stk. afkom, af hvilke 16 er OCD fri.
0,7 + [(20*0,20*,5)/(1+19(,20*,25))]*(0,8-0,7) = 0,80
4 Sikkerhed kvadreret ved avlsværdiberegning i de 5 tilfælde:
h2 0,05 0,1 0,2 0,4 0,6
-------------------------------------------
1) 0.05 0.10 0.20 0.40 0.60
2) 0.15 0.27 0.45 0.66 0.78
3) 0.17 0.20 0.22 0.23 0.24
4) 0.11 0.20 0.34 0.52 0.63
5) 0.71 0.83 0.91 0.95 0.97
Heritabilitetens størrelse har mindre betydning for
avlsværdiindekset sikkerhed, når der er mange målinger, end
ved færre målinger.
5 Formel for avlsværdi indeks og sikkerheden kvadreret for individer
med information fra, populationsgennemsnittet betegnes P,bar:
1) egen præstation (P) og a'=1 a= -
P,bar + [(1*h2*a')/(1 + 0*( ))]*(P -P,bar)
= P,bar + h2 *(P -P,bar)
r2AI = h2
2) de to forældres præstationer (P,gns) og a'=1/2 a= 0 n=2
P,bar + [(2*h2*a')/(1 + 1*(0))]*(P -P,bar)
= P,bar + h2 *(P,gns -P,bar)
r2AI = h2/2
3) de fire bedsteforældres præstationer (P,gns) og a'=1/4 a=0 n=4
P,bar + [(4*h2*a')/(1 + 3*(0))]*(P -P,bar)
= P,bar + h2 *(P,gns -P,bar)
r2AI = h2/4
4) de otte oldeforældres præstationer (P,gns) og a'=1/8 a=0 n=8
P,bar + [(8*h2*a')/(1 + 7*(0))]*(P -P,bar)
= P,bar + h2 *(P,gns -P,bar)
r2AI = h2/8
Resultaterne viser, at forventningen til avlsværdien er den samme
i de fire tilfælde, men sikkerheden falder drastisk jo længere man
kommer ud i stamtavlen.
Løsninger, Lektion 8, link opgaver
1 Respons ved individuel selektion måles som: R = h2(SFædre + SMødre)/2 Indsættes i formel får man R = 0,3[(1008-935) + (970-935)]/2 = 16 gram Den gennemsnitlige tilvækst der forventes for afkommet er 935 + 16 = 951 gram. 2 Ved tabelopslag findes 'i' når der bruges 5% hanner til avl er i = 2,06 og 33% hunner til avl er i = 1,10 S beregnes som i*sigmaP for hanner til 2,06*0,3 = 0,618 og hunner til 1,10*0,2 = 0,220 Den genetiske ændring i krops størrelse man forventer pr. generation R = 0,4(0,618 + 0,220)/2 = 0,17 kg 3 Det antages, at en population af høner har en årlig gennemsnitsydelse på 230 æg. Den fænotypiske standardafvigelse er 35,7 æg. Der regnes endvidere med en heritabilitet på 0,40 for årlig ægydelse. Selektionen baseres udelukkende på høner, og 20 procent af de højestydende høner benyttes til avl. Beregn følgende: a) Selektionsdifferencen (antal æg) er i*sigmaP = 1,4*35,7 = 50 'i' er funden ved tabel opslag. b) Den genetiske ændring (antal æg) fra moder til datter- generationen. R = 0,4(0 + 50)/2 = 10 æg c) Døtrenes gennemsnitlige ægydelse pr. år forventes at blive: 230 + 10 = 240 æg 4 Hoftedysplasi hos hunde er en tærskelegenskab med en heritabilitet på h2 = 0,3. Ca. 30% af alle Schæferhunde har hoftedysplasi. De 70%, der er fænotypisk raske, har tilsyneladende ens avlsværdi, hvis man udeluk- kende baserer avlsværdien på grundlag af røntgenbilleder af de pågældende hunde. a) Når der blandt de 70% raske Schæferhunde udtages en tilfældig stikprøve, svarer det til at der udtages 70% til avl: i=0,50 b) Når man anvender de 70% raske Schæferhunde til avl bliver: delta G = i*h2*sigmaP = 0,5*0,3*sigmaP = 0,15 sigmaP-enheder c) Når der bruges 10% hanner til avl er i= 1,75, og 70% hunner til avl er i= 0,5. VA = VP*h2svarende til sigmaA = 0,55*sigmaP rAI = 0,79 delta G = (1,75*,79*,55*sigmaP + 0,15*sigmaP)/2 = 0,46*sigmaP d) Forholdet mellem delta G beregnet under punkt c) og b) er: En forbedring på 3 gange. 5 Antal afkom pr. fader der skal afprøves optimeres så den genetiske ændring pr. generation er størst mulig. Da stationen har en bestemt størrelse og der skal bruges et bestemt antal til avl, er det forholdet mellem intensitet og sikkerhed, der skal optimeres. Der opstilles en tabel der har gruppestørrelse (n) som variabel. n til avl i * rAI -------------------------------------------- 1 40/800 2,06 * 0,224 = 0,461 2 40/400 1,76 * 0,308 = 0,540 3 40/266 1,58 * 0,369 = 0,583 4 40/200 1,40 * 0,416 = 0,583 5 40/160 1,28 * 0,456 = 0,584 6 40/133 1,16 * 0,490 = 0,568 7 40/113 1,07 * 0,519 = 0,555 F.eks. for n=4 kan der testes 200 hanner heraf skal der bruges 40 til avl, hvilket svarer til 20%, der ved opslag giver i=1,40. Det bedste resultat fås for n lig 5, men toppunktet er meget fladt. 6 a) Der er to fænotyper der kan tilskrives værdierne 0 og 4, hvilket svarer til den nævnte effekt. Da der er fuldstændig dominans, er frekvensen af de to fænotyper 0,25 og 0,75, hvilket svarer til en middelværdi på 3. Varians beregnes som de vægtede afvigelsers kvadrat: 32*0,25 + 12*0,75 = 3.0 Genets bidrag til den samlede additive varians er 3 procent b) Kommentarer til hvornår det er formålstjenligt at anvende genmar- kører: Andel af egenskabens additive varians skal være ret stor, meget større end de tre procent i nærværende tilfælde. Heritabiliteten for egenskaben skal endvidere være lav, dvs. af størrelsorden 10 % eller mindre. 7 a) Ved et selektionseksperiment med mus kan den genetiske korrelation mellem tilvækst og kuldstørrelse beregnes som forholdet mellem de standardiserede direkte og indirekte selektionsrespons: rAx,Ay = (0,693/0,88)/(2,34/1,13) = 0,38 idet sigmaAx = 1,13 og sigmaAy = 0,88 b) Selektionsintensiteten ix beregnes ved hjælp af formlen for delta G, den gælder for selektion over en generation. Derfor skal R divideres med 9. R = S*h2 = h2*i*sigmaP = 2,34/9 gram, svarende til i=0,48
Løsninger, Lektion 9, link opgaver
1 a) Indavl reducerer frekvensen af heterozygoter og øger tilsvarende frekvensen af homozygoter i forhold til H-W ligevægt. Den gennemsnitlige vægt under indavl på F=0,25 og Fpq=0,04 er: 100*(,64+Fpq) + 80*(,32-2Fpq) + 50*(,04+Fpq) = 91,2 gram b) Den gennemsnitlige vægt uden indavl er: 100*,64 + 80*,32 + 50*,04 = 91,6 gram Indavlsdepressionen er 0,4 gram 2 a) Graden af heterosis ved krydsninger er i procent: 1) ikke-indavlede 100*(22,8-(22,7+20,1)/2)/((22,7+20,1)/2)= 6,5% 2) indavlede 100*(19,9-(21,7+13,1)/2)/((21,7+13,1)/2)= 12,6% b) Indavlsdepressionen er nedgang i middelværdi ved indavl. Indavlsdepressionen udtrykt i procent for: linie A 100*(22,7-21,7)/22,7 = 4,4% linie B 100*(20,1-13,1)/20,1 = 34,8%