Cuando un menor material está accesible a la segregación mendeliana, hipótesis alternativa suele ser posible, que no pueden ser excluidos. La segregación puede, como se mencionó anteriormente, también se causado por la genética simulada (fenocopias) o la herencia umbral, donde la segregación puede parecerse a la herencia mendeliana simple. Si una hipótesis dada es para ser aceptada, el prueba apareamiento es en muchos casos, simplemente esperando a tener más descendencia a nacer, en el que los resultados son predecibles. Si los resultados se desvían, una nueva hipótesis, que puede ser probada, tiene que ser formulada.
¿Cuántos datos se necesitan para una prueba determinada para dar una respuesta final?
Esta es una de las cuestiones importantes que tienen que ser respondidas antes del inicio de la prueba de apareamiento.
Prueba de apareamiento de un toro, que es un portador sospechoso, se puede hacer en el apareamiento con el toro y vacas afectadas, transportistas o hijas del toro. Teniendo en cuenta estos casos, ¿cuántos hijos normales tienen el toro produje antes de que pueda ser declarado no afectada? La probabilidad de que un descendiente normal es nacido en los tres casos es respectivamente, 1/2, 3/4 y 7/8. Usando la regla de multiplicación de las probabilidades en el acoplamiento con conocidos transportistas, la probabilidad de obtener un descendiente normal es (3/4) n. Por medio de esta fórmula y un límite de la significación de 0,05, 0,01 y 0,001 n puede ser calculada a cumplir los criterios de probabilidad clásica.
Número de hijos normales (n) que son necesarios para excluir un toro como portador
Exclusión de toro Probabilidad Fórmula como portador -------------------------------------- Test-apareamiento 0,05 0,01 0,001 (x)n menos de ------------------------------------------------------------------ Conocido recesiva 5 7 10 x=1/2 Conocido portadoras 11 16 24 x=3/4 Hijas 23 35 52 x=7/8 -----------------------------------------------------------------
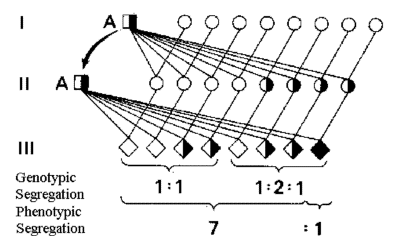
Figura 5.6 Segregación teórica de los genes recesivos en el apareamiento de prueba con hijas.
 |
Para descendencia normal de un individuo heterocigótico por el padre/hijas de apareamiento la probabilidad es de 7/8, como puede deducirse de la Figura 5.6. El número de hijos necesarios para declarar el padre no-portador sobre el nivel del 5 porciento (7/8)n = 0,05 correspondiente a n * ln(7/8) = ln(0,05), que redondeado es n = 23.
Apareamiento con las propio hijas también tiene la ventaja de que el toro se comprobará como portador de todos los posibles genes recesivos, no sólo el que es sospechosa de haber.
Test de Ji-cuadrado
En las pruebas de las proporciones de segregación para conocer el acoplamiento un test de Ji-cuadrado puede ser utilizado. El prueba para unirse con conocidos portadores se asemeja a la prueba para el equilibrio H-W, pero aquí los números esperados son en las proporciones 1:2:1 para el codominante, y 3:1 para los casos dominante. El número esperado se calcula multiplicando las frecuencias esperadas (proporciones) con N, como se muestra en la tabla de abajo.
Segregación en el apareamiento de prueba de Aa x Aa, herencia codominante.
--------- Genotipo AA Aa aa Total Números, obs 30 51 39 = 120 = N Frecuencia, exp 1/4 1/2 1/4 = 1,00 Números, exp 30 60 30 = 120 Desviación 0 -9 9 Ji-cuadrado 0 1,35 2,70 = 4,05 ----------
Df = 3-1 = 2, ya que el material sólo se proporciona el parámetro N para el cálculo de las cifras previstas. El valor Ji-cuadrado es menor que la H0 valor de la prueba de 5,99, lo que significa que no hay desviación estadística significativa de un 1:2:1 segregación en el nivel de 5 porciento.
Segregación en el apareamiento de prueba de Aa x Aa, herencia dominante
--------- Genotipo AA+ Aa aa Total Números, obs 81 39 = 120 = N Frecuencia, exp 3/4 1/4 = 1,00 Números, exp 90 30 = 120 Desviación -9 9 Ji-cuadrado 1,00 2,70 = 3,70 ----------
Df = 2-1 = 1, ya que el material sólo se proporciona el parámetro N para el cálculo de las cifras previstas. El valor Ji-cuadrado es justo por debajo de la H0 valor de la prueba de 3,84, lo que significa que no hay ninguna desviación estadística significativa de una relación de 3:1 la segregación en el nivel del 5 porciento.
Applet para el cálculo de la Ji-cuadrado para la segregación mendeliana en el apareamiento de prueba, se encuentra aquí.