La definición de
valor de cría (A) de un individuo se basa
en un infinito número de hijos,
todos medios hermanos.
El valor de fenotipo (P) de un animal puede ser medido y evaluado como una desviación del valor esperado de la población, (P-barra).
El valor de genotipo (G) de un animal es igual al valor esperado del fenotipo de los individuos con el mismo genotipo.
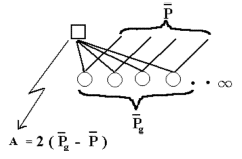
| Figura 6.1 La definición de valor de cría (A) de un individuo se basa en un infinito número de hijos, todos medios hermanos. |
 |
La definición del valor de cría (A) de un individuo se basa en un infinito número de hijos como dos veces la desviación del valor esperado de hijos del valor esperado de la población (promedio), cuando el apareamiento al azar se utiliza. Es decir, todos los hijos son medios hermanos, véase Figura 6.1.
El valor esperado de la población, P-barra, se puede añadir a los valores de cría, y así deben estar en una escala actual. La definición es válida cuando se refiere tanto a un rasgo específico, y el efecto de los genes en un único locus. Las fórmulas correspondientes a las definiciones aplicadas en los datos de un solo locus se muestran en la Figura 6.2. Es una condición previa que el locus tiene un efecto sobre el rasgo examinado y que el promedio de los animales (con diferentes genotipos) difiere de unos a otros. El promedio de la población puede ser calculado como un valor esperado. Es decir, la suma de los tres genotipos multiplicado por sus respectivas frecuencias. Véase el ejemplo del peso de los ratones que se muestra en la Figura 6.2.
| Figura 6.2. Definición de la valor de cría para el genotipo A1A1 y es ejemplificado por el peso de los ratones en función de los genotipos en un locus. Un varón con el genotipo A1A1 se tiene un número infinito de descendencia después de apareamiento al azar en una población. |
 |
Cuando un animal A1A1 se somete a apareamiento al azar en una población, el animal puede obtener dos tipos de hijos, A1A1 y A1A2, que se ve en Figura 6.2. El gen de la población determinó el genotipo en la descendencia. Las frecuencias de los dos genotipos posibles son iguales a las frecuencias de la población p y q.
El valor esperado (ingles mean value) de una población o de la descendencia de A1A1 se calcula como:
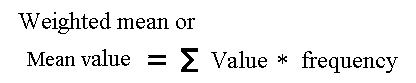
En el ejemplo del peso de los ratones (Figura 6.2), el cálculo del valor esperado de la población (P barra) y el valor de cría para el genotipo A1A1 se muestra. Un valor genético similar puede ser calculado para el genotipo A2A2, que, por el apareamiento al azar en la población, los descendientes son de los tipos A1A2 y A2A2 con las frecuencias p y q. Estos resultados se derivan de la Figura 6.2 con el apareamiento de la población con el A2A2 en vez de A1A1. El valor de cría de A2A2 es 2(12*0,3+6*0,7 - 9,24) = -4,88.
Los valores genéticos de los heterocigotos son el promedio de los dos genotipos puros, como la mitad de sus gametos es A1 y la otra mitad es de tipo A2. Los valores genéticos a menudo son llamados los valores aditivos, ya que son proporcionales al número de A1 genes en el genotipo.
Si el valor de genotipo (G) es dominante más o menos claro,
el valor esperado de un
genotipo específico no es igual al valor de cría (A). Sin embargo, habrá un
resto que es causada por las desviaciones de dominancia (D).
El grado de dominante está determinado por el valor del tipo de heterocigotos
en comparación con el promedio de los dos homocigotos:
Un ejemplo de cálculo del valor de cría (A) y las desviaciones de dominancia (D)
Abajo se muestra los resultados de un ejemplo de la variación en el locus de la transferrina. En vacas Yérsey
el genotipo TT
rendimiento de 2082 kg leche y las vacas con los genotipos Tt y de los rendimientos TT 1882 kg. leche.
Abajo se presentan las cifras reales, el cálculo del valor esperado se basa en las
frecuencias génicas p y q, que son, respectivamente, 0,67 y 0,33.
Genotipo TT Tt tt ----------------------------------------------------------- Kg leche 1882 1882 2082 (Genotipo)frecuencias p2=0,45 2pq=0,44 q2=0,11 Y valor esperado = 0,45*1882 + 0,44*1882 + 0,11*2082 = 1904 kg
Los valores de cría se calculan como desviaciones del valor promedio de la población, véase escala:
TT y Tt Valor promedio tt
1882 1904 2082 Escala original,kg
---|-------|---------------------------|--> Escala de genotipos
-22 0 178 Desviación de promedio
Genotipo valores de cría
--------------------------------------------------
TT p Tt q
TT 2*[(-22*0,67 + -22*0,33) - 0] = -44
Tt = 22,6 Promedio de los homocigotos
tt 2*[(-22*0,67 + 178*0,33) - 0] = 89,2
--------------------------------------------------
Con el apareamiento al azar en la población el genotipo TT tiene descendientes que son de los tipos de TT y Tt, con la frecuencias de p y q. Esto puede derivarse de Figura 6,2.
Los valores de genotipo se fijan como las desviaciones de la media de la población (véase la escala). Y los valores de cría son calculados de acuerdo con la definición. Por último, las desviaciones de dominancia (D) se pueden determinar como un resto, como se muestra por debajo.
Genotipo G = A + D ------------------------------------- TT -22 = -44 + 22 Tt -22 = 22,6 + -44,6 tt 178 = 89,2 + 88,8 -------------------------------------
Los resultados derivados de la utilización del applet en el ejemplo de los pesos en los ratones se muestra en la Figura 6.2
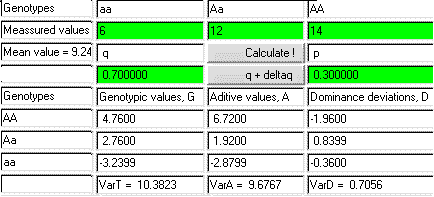 |
Es posible calcular la varianza de un locus. La diferencia esta causada por las diferencias en los valores de cría o en las desviaciones dominantes. La varianza (V) se calcula como un suma de valores de cría cuadrado * su frecuencia. Por ejemplo, la varianza de los valores de cría de: VA = (-44-0)2*0,45 + (22,6-0)2*0,44 + (89,2-0)2*0,11 = 1926, que, en este caso, es el valores de cría al cuadrados multiplicado por su frecuencia del genotipo. El promedio de los valores de cría puede ser calcula como un valor esperado -44*0,45 + 22,6*0,44 + 89,2*0,11 = 0, es cero, lo que era de esperar.
Un applet para el cálculo de G, A y D son mostrado en la figura de arriba y se encontró
aquí
Experimentos para determinar los efectos de genes cuantitativos se describen en el capítulo 12. Loci,
que tiene efecto sobre un rasgo cuantitativo, a menudo son llamados (QTL, en ingles Quantitative Trait Loci).