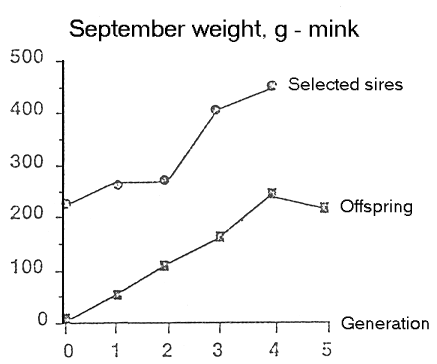
Figure 6.5. Example of selection experiment on which
calculation of heritability can be based.

Figure 6.5. Example of selection experiment on which calculation of heritability can be based. |
R = h2*S can also be interpreted as the regression of offspring on the average of the two parents, where the regression coefficient b correspond to h2.
Heritability estimation based on calculated correlation. The use of a selection experiment for estimating the heritability takes long time, at least several generations. Now will be presented methods for estimation of the heritability based on data from one generation only.
The heritability (h2) can be estimated as the calculated correlation (r or t) between related individuals divided by the coefficient of relationship (a). This is correct if inheritance (genes) is the only cause of similarity between the involved individuals. The formulas are as follows:
h2 = r/a, or r = a*h2.
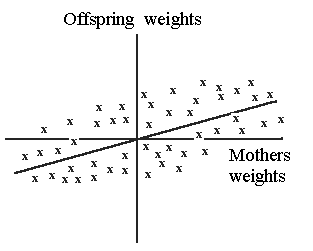
The calculation of the correlation can be done according to the classical method (see Figure 6.4). When considering several individuals in a group, as for instance half sibs, calculations are done by means of analysis of variance and estimation of the interclass correlation.
| Figure 6.4. An example of a two-dimensional distribution for calculation of correlation, typically a trait of a mother and one of its offspring. |
 |
Estimation of the heritability can be based on full and half sib material as can be found in all multipare species. The heritabiliy measures what degree of similarity exists between related animals sharing identical genes.
If environmental factors are causing the similarity, this can be estimated as shown in the formula below. The common environmental factors are particularly important in the litter's first months, when the mother and its maternal abilities cause the special environment. In half sibs, having a common father, the common genes are usually the only cause of similarity.
The general formula for interpretation of correlation between related individuals is shown below, and as symbol of this correlation t is used, this is also the symbol of the interclass correlation.
t = a*h2 + c2
Now the heritability can be calculated on the basis of half sib correlation, c2 being 0. Then c2 for full sibs can be calculated based on the full sib correlation.
Example: Weight of mink aged 8 weeks, sample size: 508 animals in 107 litters with 37 sires.
In a statistical analysis of the weight of 508 mink puppies was recorded.
Half sib correlation t = 0.03 and
Full sib correlation t = 0.41.
These numbers put into the genetic model results in:
Half sib correlation t = (1/4)*h2 + 0 = 0.03 corresponding to h2 = 0.12.
Full sib correlation t = (1/2)*h2 + c2 = (1/2)*0.12 + c2 = 0.41 corresponding to c2 = 0.35. For calculation of c2 for full sibs
the heritability calculated for
half sibs is applied.
There is a very low heritability of growth in this early age, where the maternal factors play a large role. To see the statistical calculation of the estimated weight of the mink click here.
The material for calculation of heritability of height of humans was shown in
chapter 1. As mentioned there, the heritability was calculated as the
regression of offspring on basis of the average of the parents. For height of humans it was around 0.6.
Mother-offspring correlation was found to be 0.4 while the correlation between father
and offspring was only 0.2. This lower correlation between father and offspring might be
caused by the fact that these do not share the same significant common environment as
the mother and offspring. The 0.2 correlation between father and
offspring gives a heritability of 0.4 for height of humans. This means that the
mother-offspring correlation is highly influenced by their common environment.
For data and the applied SAS program for height of humans, material from 2000, click here.
Further examples of application of the analysis of variance for calculating the repeatability coefficient for litter size of mink and heritability for the body length of swine. For the SAS program and the mink material, click here and for the swine material, click here