Når der arbejdes med feltdata, og når det drejer sig om nye sygdomme, er det nødvendigt at arbejde med familier, hvori sygdommen optræder. Når man på grundlag af sådanne observationer vil beregne om udspaltningen stemmer overens med Mendelsk arvegang, er det nødvendigt at korrigere for de familier der kunne spalte ud, men på grund af tilfældigheder ikke gør det.
| Figur 5.7 |
 |
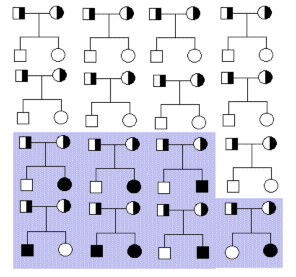
Er der tale om recessiv arvegang og man har en familie, hvor begge forældre er heterozygote, vil der være 3/4 chance for at familien ikke bliver afsløret på grund af sygt afkom, efter det første afkom er født. Efter andet afkoms fødsel vil chancen være (3/4)2 = 9/16. I nedenstående figur er vist, hvorledes heterozygote forældre vil spalte ud i en familiestørrelse på to. I de 9 ud af 16 familier vil der ikke være afficeret afkom, så når de ikke medtages i den endelige analyse, bliver den klassiske Mendelske analyse meningsløs.
I det følgende er vist formler for test og beregning af korrigeret udspaltningsforhold fra familier med udspaltning. Relevante data (skraveret område) fra figur 5.8 er derfor:
T = 14 -total antal A = 8 -antal afficerede A1 = 6 -antal familier med 1 syg A2 = 1 -antal familier med 2 syge
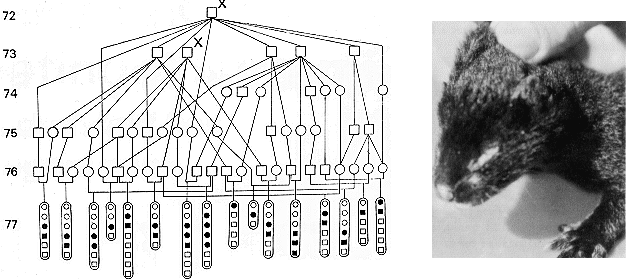
I figur 5.8 er vist et pilediagram over minkfamilier fra en farm, hvor der har været et stort udbrud af tyrosinæmi. Et af de kliniske symptomer er som vist på billedet, at øjenlågene klistrer sammen. Hvalpene dør efter en til to dages sygdom, tilfældene optræder ved en alder af ca 6 uger. En detaljeret beskrivelse af sygdommen foreligger i Christensen et al. Canadian J. Comparative Medicine, 43:333-340, 1979.
Figur 5.8. Udspaltning af tyrosinæmi i en minkbestand (fyldte symboler),
billedet til højre viser en angrebet minkhvalp med de typiske tilklistrede øjne.
De formler der skal anvendes ifølge "Singles metode" for test om Mendelsk
nedarvning (for proportionen p-hat) er vist i nedenstående figur.
Der er tillige anført tal fra ovenanførte mink tyrosinæmi tilfælde
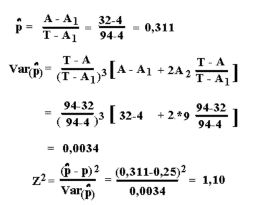
I ovenstående mink familie findes ved optælling at:
T = 94 -total antal hvalpe A = 32 -antal afficerede A1 = 4 -antal familier med 1 syg A2 = 9 -antal familier med 2 syge
Beregningerne er anført i ovenstående figur. Der er ikke signifikant afvigelse fra en 3 til 1 udspaltning da testværdien er mindre end 3,84 (H0: p(hat) = p =0,25). Bemærk endvidere at familier med mere end 2 syge ikke direkte indgår i beregningerne, men kun bidrager til totalt antal afficerede. En applet til brug ved beregningerne kan kaldes her
Indsættes tallene fra det første teoretiske eksempel (Fig. 5.7) i formlen for p(hat) får man (8-6)/(14-6) = 0,25, hvilket naturligvis er det korrekte resultat, idet data stammer fra parring af kendte heterozygoter.