Populationer: Hunde 500, katte 500, Heste 100, Får 100 og produktion per år Kvæg 1000, Fjerkræ 120000, Grise 20000, Mink 10000
(alle i 1000)
Fisk 40, Smør 100, Ost 300, Oksekød 300
(alle i 1000 tons)
1. Introduktion, kvantitativ kontra kvalitativ genetik
2. Hardy-Weinberg loven for genfrekvens stabilitet i stor population
3. Afvigelser fra Hardy-Weinberg ligevægt
5. Test af simple genetiske hypoteser, eksperimentelle eller feltdata
6. Definition af kvantitativ egenskab, avlsværdi og heritabilitet
8. Genetisk ændring ved selektion
10. Kromosomer og kromosomfejl
11. Farvegenetik
12. Beregnings- og bioteknologi herunder genmarkører og sygdomsresistens
13. Opgaver og løsningsforslag
14. Genetic calculations, applets and other programs (in English)
15. Input to genetic discussion club or former input (in English)
Nærværende genetiknoter er fremstillet som afløsere for 'Veterinary Genetics' af FW.Nicolas, Oxford University Press, 1989. Denne bog udgik af trykken i 1995.
Da noterne er skrevet til et kursus for veterinærstuderende satses der dels på at bibringe læseren forståelse af den biologiske baggrund for genetikken og dels på at tilvejebringe et minimum sæt af formler, der beskriver sammenhæng mellem praktiske observationer og genetisk teori. Udover egenskaber med simpel Mendelsk arvegang er der lagt vægt på den genetiske baggrund for egenskaber (sygdomme) med multifaktoriel ætiologi, hvor det ved anvendelse af korrekte avlsplaner er muligt, at nedsætte sygdomsforekomsten væsentligt.
Genetiknoterne ligger på instituttets KVL kursus server og kan nås via et link på adressen www.ihh.kvl.dk/htm/kc/popgen/genetik/genetik.htm. Online ligger tillige en voice version, hvortil der er knyttet overhead serier. Voice versionen er udarbejdet af undertegnede, og de studerende Anders Birk, Charlotte Jespersen, Pil Larsen, Mette Jensen, Troels Lind og Thomas Mark. andre servere og til udvidede beregnings eksempler og edb programmer (appleter).
Opgaver og løsningsforslag er for en dels vedkommende taget fra Opgaver i Husdyrgenetik 1985, hvor lektor Hanne Østergård var medforfatter. Opgaverne er tilpasset nærværende noter såvel som til Veterinary Genetics, der er tillige et eksempel og en eller flere opgaver til løsning med hver af appleterne ('regneark' i online versionen).
Professor Merete Fredholm takkes for inspiration og mange gode forslag til forbedringer, og Lektor Peter Sestoft takkes for hjælp i forbindelse med etablering af appletterne.
Fem veterinærstuderende, Tina Pihl, Camilla Gyhrs, Eva Løber, Gunhild R. Pedersen og Gorm K Carson, takkes for kritisk gennemlæsning og forslag til forbedringer. De har haft en vigtig forudsætning, da de har været i processen med at lære stoffet. Er der andre, der har forslag til rettelser eller forbedring, modtages disse med tak.
6.udgave maj 2003 Knud Christensen
Falcorner,D.S. & Mackay T. 1996. Introduction to Quantitative Genetics. Longman Scientific & Technical
Nicolas, F.W. 1989. Veterinary Genetics. Oxford University Press
Nicolas, F.W. 1996. Introduction to Veterinary Genetics. Oxford University Press
Samuel, M. 1989. Statistics for the life science. Prentice-Halls
Strachan, T. & Read A.P. 1996. Human Molecular Genetics. John Wiley & Sons, pp 597.
Juristens udlægning af Mendels love af Erik Bahn
Pdf fil af Genetik noter
Pdf fil af Genetik noter, lille format
1. Husdyrhold i danmark, kvantitative egenskaber
2. Begreberne phenotype og genotype samt arvelighedsgrad
3. Effekt af avlsarbejde (evolution)
4. Overgang mellem kvantitativ og kvalitativ nedarvning
5. Kvalitative egenskaber, Mendelsk genetik
6. Eksempler på Mendelsk nedarvning
- Lyd og billed show (real player should be installed)
eller Billed show
Danmark er et landbrugsland med et intensivt husdyrbrug. Der drives intensiv avl med de fleste husdyrarter.
Avlen benytter metoder, der svarer til naturlig selektion med 'survival of the fittest', her er det blot avlsledelsen
der afgør hvilke dyr, der er bedst tilpassede. Der gives en introduktion til begreberne genotype, phenotype, korrelation
og lineær regression, men sammenspillet mellem dem kan først forstås til fulde, efter at man har studeret lektionerne 2 til 8.
Grad af arvelighed bestemmes ved hjælp af måling af lighed (korrelation) mellem beslægtede individer. Enhver egenskab
kan klassificeres som enten kvalitative, kvantitative eller tærskel-egenskaber. Forudsigelse af udspaltning af de kvalitative
(Mendelske) egenskaber sker oftest ved hjælp af statistiske metoder, der bliver uddybet i lektion 2 og 3.
Danske Husdyr-Populationer/Produktion per år,
stærkt afrundede tal.
1. lektion. Introduktion, kvantitativ kontra kvalitativ genetik
1.1 Husdyrhold i Danmark, kvantitative egenskaber
-----
| Figur 1.1.
Populationer: Hunde 500, katte 500, Heste 100, Får 100 og produktion per år Kvæg 1000, Fjerkræ 120000, Grise 20000, Mink 10000 (alle i 1000) Fisk 40, Smør 100, Ost 300, Oksekød 300 (alle i 1000 tons) |
 |
Den summariske liste over danske husdyrproduktioner
viser, at de kvantitative egenskaber har væsentlig
betydning for produktions størrelse og økonomien i
husdyrholdet. Den samlede danske husdyrproduktion
beløber sig til ca 50 milliarder kr per år, hvoraf
størstedelen bliver eksporteret.
For verdens husdyrracer se Livestock,
Oklahoma
De fleste kvantitative egenskaber udviser en vis grad af arvelighed. Arvelighed viser sig ved at individer, der afviger positivt fra gennemsnittet, også får afkom der afviger positivt og omvendt. Der er en jævn overgang mellem egenskaber, der nedarves Mendelsk med simpel arvegang, og egenskaber der udviser kvantitativ arvegang uden vel adskilte klasser. Den kvantitative genetiske arvegang skyldes, at effekten af det enkelte gen er ringe, og at geneffekten også er under indflydelse af miljøpåvirkninger.
Arvelighedsgraden afgør ligheden mellem beslægtede individer.
Arvelighedsgraden kan bestemmes statistisk som regression af afkom på
forældrenes gennemsnit. Arvelighedsgraden har
værdier der ligger
mellem 0 og 1, hvor arvelighedsgraden 0 svarer til ingen sammenhæng
og 1 svarer til fuldstændig sammenhæng mellem forældre
og afkom. Se højre side af figur 1.2.
Figur 1.2. Relation mellem phenotype, genotype og miljø, formuleret af W.Johannesen på grundlag af viste bønneforsøg. |
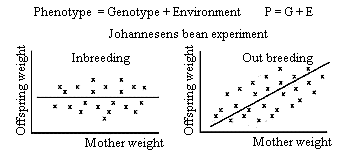 |
I ovenstående tegning er vist, hvad Johannesen fandt: Når bønnerne var 100 procent indavlede, hvilket svarer til at alle bønner genetisk set var ens, så var der ingen sammenhæng mellem bønnens egen vægt og vægt af dens afkom, regressionskofficienten (b) af afkom på forældre var lig 0. For udavlede bønner, der genetisk set alle er forskellige, var der en lineær sammenhæng b = 0,27. Dvs., var forældrebønnen 10 mg større end gennemsnittet, var afkommet 2,7 mg større end gennemsnittet.
For stort set alle egenskaber vil der i udavlede populationer være
en vis lighed mellem beslægtede individer.
I figur 1.3
er vist den todimensionale sammenhængen mellem højde blandt veterinærstuderende
og gennemsnitshøjden af deres forældre. Grafen er en udskrift fra
SAS med proceduren proc plot.
Figur 1.3 Relation for højde mellem afkom og gns forældre. Er gns. Forældre højden 1 cm over gennemsnittet er deres afkom 0,6 cm over gennemsnittet. Sammenhængen skyldes at egenskaben er arvelig med en arvelighedsgrad på 60 procent. |
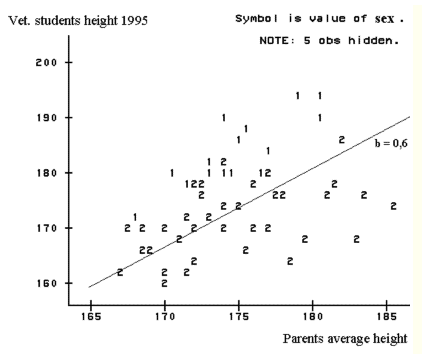 |
Genotypen kan altså kun observeres, når der er genetisk variation, og den er lig med den del af phenotypen (den phenotypiske variation) der kan genfindes hos afkom. Fra de to eksempler den udavlede bønnepopulation og den humane population kan man på grundlag af den lineære sammenhæng mellem forældre og afkom, hvor hældningen er henholdsvis 0,27 og 0,6, konkludere at genotypen (genotypisk variation) udgør henholdsvis 27 og 60 procent af den phenotypiske variation. Milieu påvirkningerne må således forårsage den resterende del af variationen.
For at få en forståelse for avlsarbejdets idé er
vist i figur 1.4, hvorledes man gennem
en lang årrække
har arbejdet med Dansk Jersey malkekvæg.
Der er gennem ca. 20 generationer
hele tiden udvalgt de dyr, der havde den højeste fedtprocent. Effekten
er ca. 0,1 procent enheders ændring per generation i fedtprocenten.
Der er ikke noget der tyder på, at man ikke kan fortsætte endnu
20 generationer med samme selektionseffekt for en højere fedtprocent.
Eller man ved selektion vil kunne nå tilbage til udgangspunktet.
Holstein Frisian (HF) racen har ikke været selekteret for fedt
% og har derfor været forholdsvis stabil i samme periode
med hensyn til fedt procent.
Figur 1.4. Fordelingskurver over fedt procent i mælken hos HF og Jersey, Jersey både år 1900 og 1990 . En Jersey ko er vist på billedet. 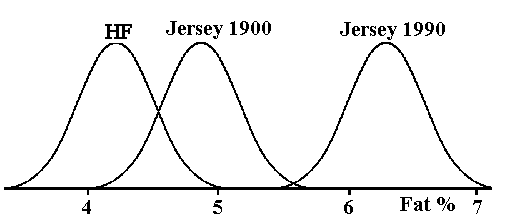 |
 |
Figur 1.5
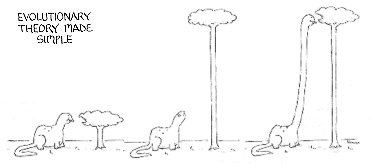 |
Avlsarbejde såvel som naturlig selektion er tidsmæssige langsomme processer. Under stærk selektion kan en populations middelværdi dog ændre sig med op til 10 procent pr generation, såfremt den givne egenskab udviser en høj arvelighedsgrad.
Resultatet af 30 generationers fortsat selektion for kuldstørrelse hos mus kan ses her. Kuldstørrelsen er ved selektion i denne periode forøget med 5 unger fra 9 til 14 pr kuld, hvilket svarer til en stigning i kuldstørrelse på 0,16 unge pr generation.
Der er en jævn overgang mellem egenskaber,
der nedarves Mendelsk
med simpel arvegang og egenskaber, der udviser kvantitativ arvegang uden
veladskilte klasser.
Figur 1.6 Forestilling om hvorledes 1 og 2 genpar kan påvirke mælkeydelse, der må dog være mange flere genpar, da man kan fortsætte med selektion generation efter generation uden at den genetiske variation forsvinder. |
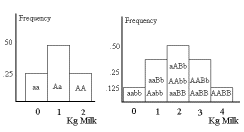 |
I figur 1.6 er vist et par tænkte eksempler hvor et eller to Mendelsk udspaltene genpar styrer mælkeydelsen, for hvert A eller B allel et individ har stiger ydelsen med et kilogram. Fordelingerne svarer til at begge alleler A og a har samme hyppighed. For at få et realistisk billede af den genetiske baggrund for mælkeydelse, må man dog regne med at den består af effekt fra flere hundrede genpar. Mælkeydelsen har ved selektion ændret sig lige så dramatisk som fedt procenten, der blev vist i foregående afsnit. For at dette har kunnet ske må der nødvendigvis være mange underliggende gener. I nærværende eksempel med kun to genpar, vil disse kunne fikseres efter en generation selektion.
Den kvantitative genetiske arvegang skyldes, at effekten
af det enkelte gen er ringe, og at de også er under indflydelse af
miljøpåvirkninger.
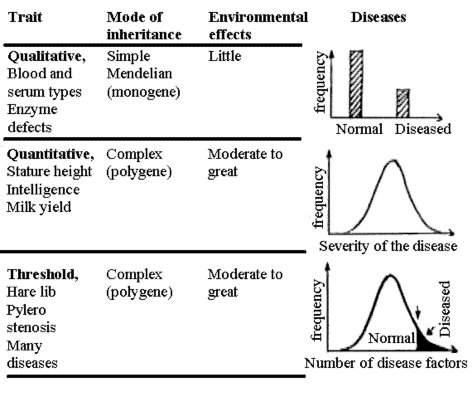
Sygdommene vil ofte være 'enten/eller egenskaber'. Der kan dog
også være tilfælde hvor en sygdoms sværhedsgrad
har en normal fordeling. For mange produktionssygdomme opstår der
først sygdom, når disponerede dyr udsættes for uheldige
mileupåvirkninger. Se Figur 1.7, der er udarbejdet
af prof.emer. Erik Andresen.
For at man for en kvalitativ egenskaber kan tale om et gen,
må der normalt være udspaltning, som der f.eks. er i pelsfarve hos Labrador
Retrieveren, hvor man har farvetyperne gul og sort. Så når man taler
om et gen for gul farve hentyder dette til både et locus og en allel.
Man kan også tale om et Albumin-gen selv om man ikke kan se phenotyperne
direkte, men som
vist i næste lektion, kan der påvises polymorfi med udspaltning af to albumin alleler
ved hjælp af elektroforese på serumprøver. Er der tale om DNA polymorfi med flere alleler
i ikke kodende sekvenser, bør man ikke anvende ordet gen. Man kan i såfald
tale om et locus med flere alleler. I praksis er der dog ikke altid en skarp skelnen
mellem gen og locus eller mellem gen og allel, så når der i næste lektion
tales om genfrekvenser, vil de omfatte
både egentlige gener og alleler i ikke kodende DNA sekvenser (loci).
Figur 1.8 Udspaltning af genetisk variation (mikrosatellit) i et lokus hos en grise familie påvist ved gelelektroforese. Ornen Cup bærer allelerne 209 og 195 og dyr 400 bærer allelerne 199 og 195. |
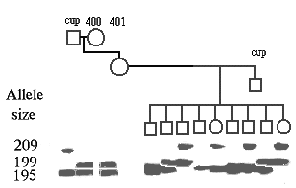 |
Ornen Cup bærer allelerne 209 og 195 og dyr 400 bærer
allelerne
199 og 195. Cup er både far og morfar til et kuld. Moderen til
kuldet 401 har fået '195' allelen fra Cup og '199' allelen fra so 400.
Det viste kuld er en del af en større familie, der indgår i et regneeksempel i
næste lektion.
For mere information om grisefamilien se
her.
 For at få et indtryk af Mendelsk arvegang inden for husdyr, kan
den australske database ANGIS anvendes, for at se den,
klik
her. Den er hovedsageligt baseret på udspaltning af sygdomsgener
i husdyrbestande. Databasen er samlet af Nicolas, der er forfatter til
Introduction to Veterinary Genetics.
Nedenstående se udskrift af litteratur fra databasen om albino genet
hos kvæg, se i øvrigt
billede
af en albino SDM kalv; udlånt af Lars Gjøl Christensen.
For at få et indtryk af Mendelsk arvegang inden for husdyr, kan
den australske database ANGIS anvendes, for at se den,
klik
her. Den er hovedsageligt baseret på udspaltning af sygdomsgener
i husdyrbestande. Databasen er samlet af Nicolas, der er forfatter til
Introduction to Veterinary Genetics.
Nedenstående se udskrift af litteratur fra databasen om albino genet
hos kvæg, se i øvrigt
billede
af en albino SDM kalv; udlånt af Lars Gjøl Christensen.
COAT COLOUR, ALBINISM in CATTLE
MIA Number : 000202
Possible human homologue (MIM number) :
[ 203100 ]
Across-Species Summary :
Congenital lack of pigment in all parts of the body. Due to a
non-functional form of the enzyme tyrosinase.
References after 1970
Greene, H.J., Leipold, H.W., Gelatt, K.M., Huston, K. (1973).
Complete albinism in beef Shorthorn calves. Journal of Heredity
64: 189-192.
Weber, W., Lauvergne, J.J., Winzenried, H.U. (1973). Hereditary
albinism in Swiss Simmental cattle [French]. Schweizer Archiv fur
Tierheilkunde 115: 142-144.
Manunta, G., Lai, P., Cancedda, M. (1975). A contribution to the
study of albinism in the Brown Mountain breed. Zootecnica e
Veterinaria. Fecondazione Artificiale 30: 129-135.
Ojo, S.A., Leipold, H.W. (1976). Ocular albinism in a herd of
Nigerian Holstein Friesian cattle. Zeitschrift fur Tierzuchtung
und Zuchtungsbiologie 93: 252-254.
Jayasekera, U., Leipold, H.W. (1981). Albinism in United States
Charolais cattle. Annales de Genetique et de Selection Animale
13: 213-218.
Foreman, M.E., Lamoreux, M.L., Kwon, B., Womack, J.E. (1994). Mapping
the bovine albino locus. Journal of Heredity 85: 318-320.
1. Gentællemetoden til beregning af genfrekvenser
2. Hardy-Weinberg ligevægt og statistisk test
4. Eksempler på anvendelse af genfrekvenser
5. Gametfrekvenser og koblingsuligevægt
6. Opgaver
- Lyd og billed show (real player should be installed) eller Billed show
Mange gener i naturlige populationer er polymorfe.
Det betyder at de har to eller flere alleler.
Hardy Weinberg loven siger, at når der er tilfældig parring
i en population, er genotypefrekvenserne for AA, Aa og aa
henholdsvis p2, 2pq og q2, hvor f(A)=p, f(a)=q. En af effekterne
af dette princip er for sjældne sygdoms alleler, at de er skjult
tilstede i stort tal hos heterozygote bærere. Kobling kan medføre
at visse alleler i to loci optræder i sammen gamet med større hyppighed
end forventet ved tilfældigheder, dette giver basis for anvendelse af
DNA markører for recessive sygdoms alleler i en population.
-----
Genetiske termer vedrørende gen og allel.
Hos Labrador Retrieveren har man farvetyperne gul og sort. Så når
man taler om et gen for gul farve hentyder dette til både et locus og en allel.
Dette svarer til den oprindelige opfattelse af gener, man har en variant (gul) i forhold
til vildtypen (sort).
Er der tale om en DNA polymorfi med flere alleler i ikke kodende sekvenser, bør man
ikke anvende ordet gen. Man bør i såfald tale om et lokus med flere alleler.
Denne sprogbrug bør også tilstræbes anvendt i forbindelse med genetiske varianter.
I praksis er der dog ikke altid en skarp skelnen mellem gen og locus eller mellem
gen og allel, så når der i denne lektion tales om genfrekvenser,
vil de omfatte både egentlige gener i traditionel forstand og alleler
i ikke kodende DNA sekvenser (loci).
Gentællemetoden, Co-dominant nedarvning, Phenotype = Genotype
Der anvendes data fra studium over albumintyper hos danske Schæferhunde, se Tabel 1 afsnit 2.4. Der er en 'fast' og en
'slow' albuminallel når serum testes på en elektroforesegel, de har allelbetegnelsen henholdsvis F og S. Undersøgelsen er
gennemført af K. Christensen et al. 1985, Hereditas, 102:219-223.
Figur 2.1. Albumintype nedarves co-dominat, dvs. begge alleler kan konstateres direkte på "phenotypen", se nærværende gel, der viser en SS en SF og en FF albumin phenotype. Gelen er efter elektroforesen af serumprøverne farvet med amidosort |
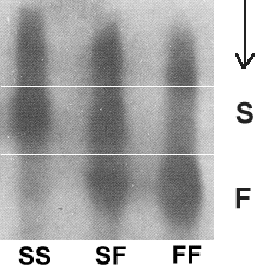 |
I populationen blev fundet følgende antal af de tre albumin genotyper.
--------- Genotype SS SF FF Total Antal 36 47 23 106 Frekvens 0,34 0,44 0,22 = 1,00 ---------- Frekvensen af SS typen beregnes som 36/106 = 0.34
Beregning af genfrekvensen for S er baseret på gentællemetoden, hvert SS individ har 2 S gener og et SF individ har 1, dette sættes i forhold til det samlede antal gener i populationen, som er 2*106.
Frekvensen af S beregnes som p = (2*36 + 47)/(2*106) = 0,56
do F do q = (2*23 + 47)/(2*106) = 0,44
------
1.00
Frekvensen af den første allel betegnes normalt med symbolet p og den anden med symbolet q. Er der flere alleler fortsættes bogstavrækken.
En allelfrekvens svarer til en sandsynlighed og summen af allel (gen) frekvenserne bliver derfor lig 1. Se iøvrigt basic statistical formulations, eller Samuels, Statistics for life science
Eksempel på multiple alleler (flere end to alleler)
I foregående lektion 1.5 blev omtalt udspaltning af en mikrosatellit i en svinefamilie, som det igen ses af nedenstående gel vist i figur 2.2, er der 3 alleler. (Udlånt af Merete Fredholm)
Figur 2.2 Udspaltning af genetisk variation (mikrosatellit) i et lokus hos en grise familie påvist ved gelelektroforese. Ornen Cup bærer allelerne 209 og 195 og dyr 400 bærer allelerne 199 og 195. De fleste dyr er heterozygote med hver to bånd. Homozygoter har kun et bånd |
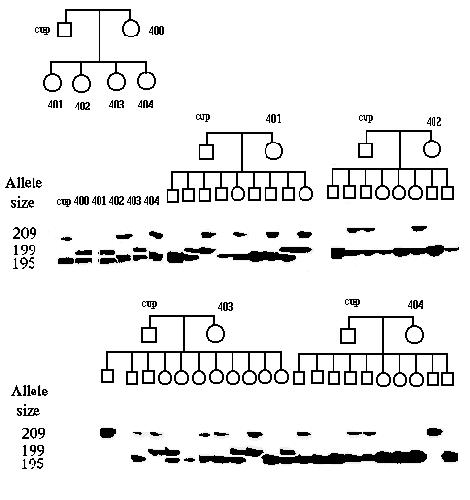
|
Frekvensen af '209' beregnes som p = (2*2 + 18)/(2*44) = 0,250 do '199' do q = (2*0 + 12)/(2*44) = 0,134 do '195' do r = 1 - p - q = 0,616
Den sidste allel beregnes nemmest som en differens, da summen af
allelfrekvenserne er 1.
Kvadratrodsmetoden, Dominant nedarvning
Figur 2.3. Labrador Retriever med normalfarvetypen sort og med udspaltning af den recessive gule farvetype. |
 |
I en population blev fundet følgende antal af de to genotyper:
--------- Phenotype Sort Gul Total Genotype EE+Ee ee Antal 182 18 200 Frekvens 0,91 0,09 = 1,00 ----------
Den sorte farvetype repræsenterer både homozygote og heterozygote. Parres to tilfældige sorte hunde, vil de engang imellem få gult afkom, hvilket skyldes en recessiv allel i extension locus. Dette sker når begge forældre tilfældigvis er af genotypen Ee.
Gentællemetoden kræver at phenotypen er lig med genotypen, hvad der kun er tilfældet for gul. For at et afkom bliver gult, skal den have et e gen fra både sin far og sin mor. Derfor kan sandsynligheds-regningens multiplikationsregel anvendes til beregning af q.
Frekvensen af ss individer svarer derfor til q2 og beregnes som 18/200 = 0,09
Tages kvadratroden af 0,09 svarer dette til q = 0,30.
Frekvensen af sort genet bliver p = 1 - q = 0,7.
Definition på H-W ligevægt. I en stor population med tilfældig sammenparring vil der efter en generations forløb opstå Hardy-Weinberg ligevægt, såfremt der er samme genfrekvens blandt han og hun køn. Hardy-Weinberg ligevægt indebærer at gen og genotypefrekvenser er konstante fra generation til generation. Opstår der uligevægt genetableres ligevægten efter en generations tilfældig parring med genfrekvenserne p og q og genotypefrekvenserne p2, 2pq og q2 i et to allelt system, når der er tilfældig parring i en stor population uden systematiske påvirkninger såsom migration, mutation og selektion.
Statistisk test for H-W ligevægt
Der anvendes data med hensyn til albumin
type hos danske Schæferhunde, der blev vist i foregående afsnit.
I populationen blev fundet følgende antal af de tre genotyper (obs), og der er beregnet
det tilsvarende forventede antal under Hardy-Weinberg ligevægt (exp).
---------
Genotype SS SF FF Total
Antal, obs 36 47 23 = 106 = N
Frekvens, exp p2 2pq q2 = 1,00
Antal, exp p2N 2pqN q2N = N
Antal, exp 33,2 52,3 20,5 = 106
Afvigelse 2,8 -5,3 2,5
Chi-i-anden 0,24 0,54 0,31 = 1,09
----------
Frekvensen af S beregnes som p = (2*36 + 47)/(2*106) = 0,56
do F do q = (2*23 + 47)/(2*106) = 0,44
-----
1.00
Det forventede antal under Hardy-Weinberg ligevægt (exp) beregnes på grundlag af
sandsynligheds
regningens multiplikationsregel.
For SS genotypen skal der trækkes et S gen fra en far, og der skal
trækkes et S gen fra en mor,
det samme gentages 106 gange. Den samlede sandsynlighed for SS genotypen
bliver derfor p*p*106. Og der gennemføres tilsvarende argumenter for de to
andre genotyper. Resultaterne er vist i ovenstående tabel.
Chi-i-anden test for H-W-ligevægt kan nu beregnes som summen af afvigelsernes
kvadrat hver i forhold til det forventede antal.
Testen har 1 frihedsgrad, da der er tre klasser, og der skal anvendes 2 frie parametre
p og N for at beregne det forventede antal. Den sidste parameter (q), der anvendes, er
ikke fri, da den kan beregnes som (1 - p).
Ved tabelopslag (kapitel 13) med 1 frihedsgrad får man, at 3,84 er 5% grænse for opretholdelse af H0, at data har H-W proportioner. Den fundne afvigelse mellem observeret og forventet antal har derfor en sandsynlighed der større end 5 %. Konklusion: Der er ikke nogen statistisk sikker afvigelse fra H-W ligevægten.
Applet til beregning af Chi-i-anden for H-W-ligevægt, klik her.
En af forudsætningerne for H-W-ligevægten er, at der er tilfældig parring i populationen. Der opstår i sådanne populationer altid genetisk ligevægt efter en generations tilfældig parring. Forudsætningen er, at der er samme frekvens hos hanner og hunner.
Ved kønsbunden nedarvning etableres der ikke nødvendigvis samme frekvens hos hanner og hunner efter en generations tilfældig parring, idet de to køn får deres gener fra to forskellige kilder.
Hos pattedyr får hannerne alle de kønsbundne gener fra deres mødre, hvorimod hunnerne får deres gener med halvdelen fra fædre og halvdelen fra mødre. Hos fugle er det omvendt, idet det er hunnerne, der er det heterogametiske køn.
Eksempel, orangegenet hos katte: I en population blev fundet følgende antal af de tre genotyper, hvor orangegenet (O) giver gul farve. Genotypen Oo giver en blandingsfarve, der er forårsaget af den tilfældige X-kromosominaktivering hos XX individer.
--------- ------ hunner --------- ----- hanner ----- Genotype OO Oo oo Total O o Total Antal 3 53 117 173 28 149 177 Frekvens 0,02 0,31 0,67 = 1,00 0,16 0,84 = 1,00 ----------
Kønsbundne gener hos pattedyr viser genet direkte hos hanner, dvs. genotypefrekvens er lig genfrekvens. Hos hunnerne derimod er beregning af genfrekvens identisk med beregning som for autosomale gener, som vist.
Frekvensen af O beregnes som p = (2*3 + 53)/(2*173) = 0,17
do o do q = (2*117+ 53)/(2*173) = 0,83
------
1.00
Som det ses, er der en ringe forskel mellem frekvensen hos han og hunkøn. Er der en forskel halveres den for hver generation med tilfældig parring, så H-W ligevægt vil derfor i praksis være genetableret efter få generationer, såfremt populationen er kommet ud af ligevægt. Phenotypisk er heterozygoten dog speciel, da kun det ene gen virker i hver enkel celle. Phenotypen opstår som følge af en tilfældig opblanding af celler med alternativt aktive gener.
Hele det ene X-kromosom er inaktivt, hvilket kan ses i kromosompræparat, figur 2.4, fra grise. Til højre ses et billede af en heterozygot hunkat med genotypen Oo. Den har pletter af gul og pletter af sort som skyldes alleler i det kønsbundne orange locus. Den hvide farve skyldes et autosomalt gen for brogethed.
Figur 2.4 Heterozygot hunkat med genotypen Oo i det kønsbundne Orange lokus.Foto Bodil Andersen, Bogense. Det giver blandingsfarven gul og sort med varierende pletstørrelse. Dette skyldes tilfældig inaktivering af det ene X-kromosom hos pattedyr hunkøn. Se det inaktive X-kromosom med en cirkel omkring. |
 . .
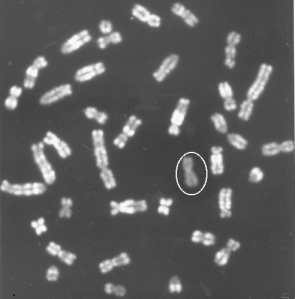
|
Det inaktive X kromosom er påvist ved en Acridin orange farvning på celler, der har været dyrket i 6,5 timer med BrdU (Brom deoxy-Uridine). DNA-syntese, der foregår efter tilsætningen, kan ses som svagt farvede områder på kromosomerne; der er en cirkel om det inaktive X kromosom. Man ved i øvrigt, at de aktive gener replikerer tidligt i cellens cyklus, og de findes derfor i de hvide bånd. hankøn. Blødersygdom (hæmofili) hos mennesker er et af de mest kendte eksempler på kønsbunden recessiv nedarvning, hvor frekvensen hos drenge er 100 gange større end hos piger. Dette opstår når genfrekvensen er 0,01, hvilket svarer til frekvensen hos drenge. Hos piger derimod skal genet komme fra både far og mor med hver en sandsynlighed på 0,01; dette svarer til en hyppighed hos piger på 1 blandt 10000.
Når man kender genfrekvenserne i en population kan man beregne genotypefrekvenserne for de enkelte genotyper under forudsætning af H-W-ligevægt. Der kan tilsvarende beregnes parringstype frekvenser under tilfældig sammenparring ved hjælp af sandsynlighedsregningens multiplikationsregel og man får, idet det skal bemærkes, at når de to genotyper er forskellige ganges der med 2, da de kan kombineres med de to typer i modsat rækkefølge.
| Afkom udspaltning | |||||
| Parringstype | Frekvens | AA | Aa | aa | |
| AA x AA | p2 x p2 | = p4 | 1 | ||
| AA x Aa | 2 x p2 x 2pq | = 4p3 x q | 0,5 | 0,5 | |
| Aa x Aa | 2pq x 2pq | = 4p2 x q2 | 0,25 | 0,5 | 0,25 |
| AA x aa | 2 x p2 x q2 | = 2p2 x q2 | 1 | ||
| Aa x aa | 2 x 2pq x q2 | = 4pq3 | 0,5 | 0,5 | |
| aa x aa | q2 x q2 | = q4 | 1 |
Beregning af parringstypefrekvenser er vigtige i forbindelse med kontrol af monogenetiske arvelige sygdomme. Dette emne
behandles indgående i lektion 5, hvor de klassiske udspaltningsforhold
hos afkom analyseres statistisk.
Applet til beregning af
parringstypefrekvenser.
Eksempel på anvendelse af appleten er vist nedenstående med q=0.005.
99% af de recessive afkom kommer fra normale forældre.
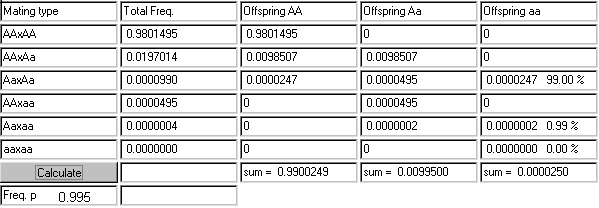
Genfrekvenser har endvidere et stort anvendelsesområde indenfor racestudier. Der er en tendens til, at genfrekvensen for nærtbeslægtede racer ligger tættere på hinanden end for fjernt beslægtede racer.
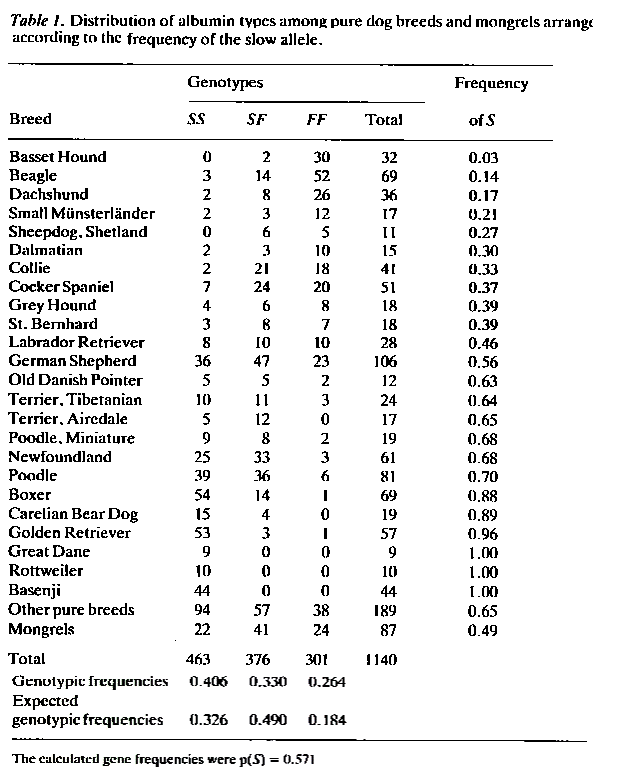
I ovenstående tabel er gengivet resultater fra studie over albumintyper hos nogle danske hunderacer. Der er en fast og en slow albumin allel, når serum testes på en elektroforesegel. De har allel betegnelserne henholdsvis F og S. Frekvensen varierer mellem hunderacerne fra 0 til 1. Undersøgelsen er gennemført af K. Christensen et al. 1985; Hereditas, 102:219-223.
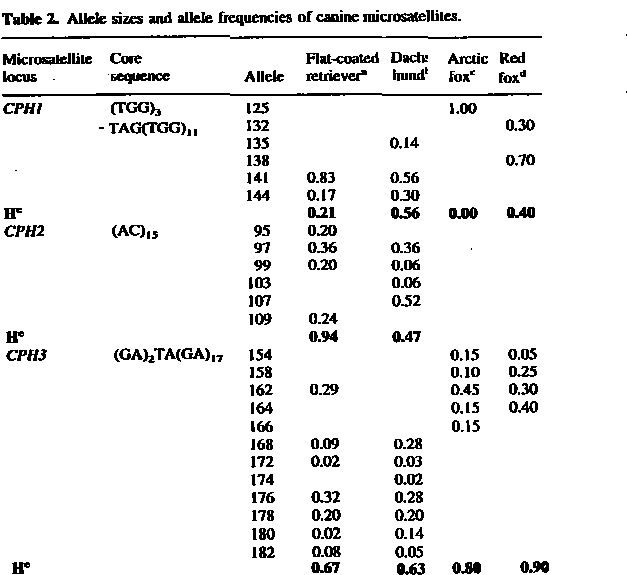
I nedenstående tabel er gengivet resultater fra studie over mikrosatelliter hos nogle danske hunderacer samt hos blå- og rødræv. Der er vist resultater fra tre systemer hver med mange alleler, der er betegnet som længden af DNA-strengen mellem de anvendte primere. Frekvensen varierer betydeligt mellem hunderacerne. Hundeprimerne virker på begge rævearter, hvilket indikerer stor genetisk homologi mellem hunde og ræve. He angiver noget om systemernes informativitet, som er afhængig af procenten af heterozygoter i den pågældende population. Genetisk set er det de heterozygote dyr, der er mest informative. Ved faderskabssager eller ved andre genetiske undersøgelse giver homozygoter ingen information om, hvilket af forældrenes gener et afkom har fået. Undersøgelsen er gennemført af M. Fredholm et al. 1995; Mamalian Genome, 6:11-18.
Gamet- eller haplotype-frekvenser anvendes, når man ser på to loci samtidig. Hver ny gamet vil indeholde en allel fra hvert locus. Ser man på to loci A og B, kan der inden for hvert loci være H-W-ligevægt, uden at det er tilfældet for de to loci tilsammen. Dette kan have stor betydning i forbindelse med DNA-markører, hvor det kan ske, at en bestemt allel altid forefindes sammen med en skadelig allel på det andet loci. Er de to loci tæt koblede, vil det vare mange generationer, før der opstår ligevægt mellem de to loci.
Definition af koblingsuligevægt og statistisk test: Vi vil nu se på de mulige gameter, der kan dannes ud fra to loci A og B med hver to alleler. Kombination af to loci A og B med hver to alleler er vist nedenfor i en klassisk tabel, hvor r, s, t, og u er de observerede gametfrekvenser af gameterne AB, Ab, aB og ab. Gameterne er opstillet i tabel som kendt fra den almene genetik, de forventede frekvenser svarer til sandsynlighedsregningens multiplikationsregel:
gamet observeret frekvens forventet frekvens afvigelse
-----------------------------------------------------------------
AB r p(A)*p(B) D
Ab s p(A)*q(b) -D
aB t q(a)*p(B) -D
ab u q(a)*q(b) D
Eksempel med statistisk test: Det observerede antal gameter er følgende: AB 6, Ab 49, aB 34 og ab 11. Den statistiske test for koblingsuligevægt illustreres bedst når tallene indsættes i den klassiske to gange to tabel med test for uafhængighed svarende til D=0. Gamet og allel-frekvenserne er anført i parenteser.
locus A/locus B B b Sum (Frek)
------------------------------------------------------------
A | 6 (r=0,06) 49 (s=0,49) | 55 (p(A)=0,55)
a | 34 (t=0,34) 11 (u=0,11) | 45 q(a)=0,45)
-------------------------------------------------------------
Sum (Frek) | 40 (p(B)=0,4) 60 (q(b)=0.6) | 100 1
Chi-i-anden = 43.1*** Df=1
D= u-q(a)*q(b)=0,11 - 0,45*0,6= -0,16
Der er statistisk signifikant afvigelse fra tilfældig kombination mellem generne A og B svarende til en disekvilibrium på -0.16. I tilfælde af en sygdomsallel store B er chancerne for at have den meget stor (34/40) når der er et lille a allel i lokus A.
Detekterbare rekombinanter: I nedenstående skema er vist de mulige genotyper i et to loci system. Dobbelt heterozygoterne er fremhævet med fed skrift. Fysisk rekombination har kun betydning hos dobbelt heterozygoterne, hos alle andre genotyper vil fysisk rekombination ikke give anledning til detekterbar rekombination. De tilsvarende forventede genotypefrekvenser under tilfældig parring fås som vist ved multiplikation af gametfrekvenserne.
gamet mor AB Ab aB ab r s t u far ------------------------------------ AB | AABB AABb AaBB AaBb r | r*r r*s r*t r*u Ab | AABb AAbb AaBb Aabb s | s*r s*s s*t s*u aB | AaBB AaBb aaBB aaBb t | t*r t*s t*t t*u ab | AaBb Aabb aaBb aabb u | u*r u*s u*t u*u
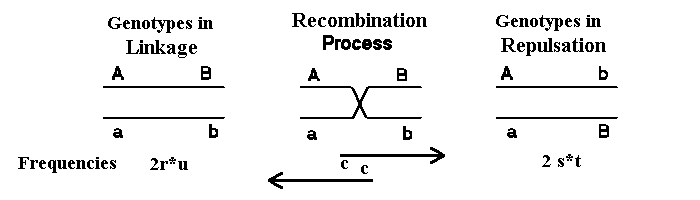
I figur 2.5 er vist de to typer dobbelt heterozygoter AB/ab og Ab/aB. Ved rekombination dannes gameter af den andens type og omvendt. Der er derfor koblingsligevægt, når der er lige mange af hver af de to typer dobbelt heterozygoter.
Dette udmønter sig i en formel mere for D som vist nedenstående.
Figur 2.5. Viser de to homologe kromosomer hos de to mulige heterozygoter i de to modsatte faser. Sker der rekombination dannes den modsattes gameter. Dette sker med frekvensen c |
 |
D = u - q(a)*q(b), eller
D = r*u - t*s (= [f(AB/ab) - f(Ab/aB)]/2)
Den maksimale uligevægt opstår, når alle dobbelt heterozygoter er i samme fase (AB/ab) eller (Ab/aB); den har da værdien DMax.
Er rekombinationsfrekvensen c, vil D formindskes til D*(1-c) per generation, så man har
i n'te generation
Dn = D0*(1-c)n, hvor
D0 er uligevægten i udgangspopulationen, se figur 2.6.
Figur 2.6. Kurver over antal generationer hen mod koblings-ligevægt for forskellige rekombinations frekvenser. |
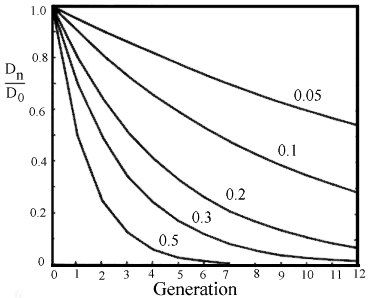 |
For to uafhængige loci med en rekombinationsfrekvens på 0,5 går der 4 til 5 generationer, før der i praksis opstår ligevægt. Drejer det sig derimod om tæt koblede loci med under 5 % rekombination, går der let 25 generationer, før man nærmer sig ligevægt, se Figur 2.6.
Der er som vist ovenstående i alt 16 genotype-kombinationer, når man trækker en tilfældig gamet fra henholdsvis far og mor hvilket svarer til de klassiske Mendelske to genspaltninger. Mendels anden lov udsiger, at der opstår koblingsligevægt i F2 i en analysekrydsning, hvilket skyldes at alle individer i F1 er dobbelt heterozygoter i den ene fase. Da det kun er dobbelt-heterozygoterne, der kan 'rekombinere', går det meget langsommere i en blandingspopulation, hvor frekvensen af dobbelt-heterozygoten kun er 2(r*u + t*s).
Opbrud af koblingsuligevægt kan give anledning til ny genetisk variation for kvantitative egenskaber. Er to gener koblede, og har de henholdsvis positiv og negativ effekt, og de sidder på samme kromosom, opstår den nye variation ved, at rekombinerer bringer de to positive gener til at sidde på samme kromosom.
I forbindelse med en ny mutation er der koblingsuligevægt i mange generationer fremover, da mutationen opstår på et og kun et kromosom. Denne koblingsuligevægt kan bruges i forbindelse med anvendelse af DNA-markører til påvisning af genets placering på et unikt kromosom og til påvisning af anlægsbærer ved hjælp af DNA-markører.
Der er altid maksimal koblingsuligevægt indenfor en familie. Dette gør det muligt at arbejde med DNA-markører indenfor familier. Er der født et sygt individ med en recessiv sygdom types dette med DNA-markørerne. Er der tæt kobling vil fremtidige afkom med samme kombination af DNA-markører med stor sandsynlighed også være syge.
Applet til beregning af Chi-i-anden for koblingsligevægt, klik her, og Applet til studie af kobling og koblingsuligevægt, klik her.
1. Systematiske avigelser fra H-W ligevægt
2. Selektion mod den recessive
3. Selektion for heterozygoter
4. Selektion mod heterozygoter
5. Tilfældige afvigelser fra Hardy-Weinberg ligevægt
6. Effektiv populationsstørrelse
7. Opgaver
- Lyd og billed show (real player should be installed) eller Billed show
Både mutationer og migration introducerer nye alleler i en population.
Mutationsraterne er almindeligvis lave, derfor bidrager mutation kun lidt
til ændring af allel frekvenser. Naturlig og menneskeskabt selektion kan
ændre allel frekvenser på en systematisk måde til fordel for en af allelerne
(genotyperne). Selektion kan også resultere i en stabil genetisk polymorfi, hvor
heterozygoten har den højeste fitness. Selektion mod skadelige mutationer kan
føre frem til en selektions-mutations balance, hvor frekvensen af den skadelige
allel forbliver konstant fra generation til generation. Den lille population er
ustabil pga. 'genetisk drift', der er forårsaget af tilfældige ændringer af
genfrekvensen. Retningen på ændringen er tilfældig, og kan være meget hurtig
i små populationer på under 100 avlsindivider.
-----
I en stor population med tilfældig parring er der H-W ligevægt, med mindre populationen er underkastet systematiske påvirkninger, der kan ændre genfrekvensen. De systematiske processer kan opdeles i følgende kategorier.
|
Figur 3.1.
Mutation, Migration og Selektion |
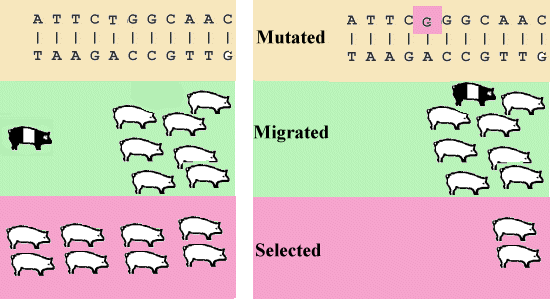 |
Mutation sker normalt med en frekvens på 1 per million gameter per gen for de egentlige arveanlæg (strukturgener). Den sker ca. 1000 gange hyppigere, når det drejer sig om antal repetitioner i korte repeterede DNA sekvenser (mikrosatelliter). Disse sekvenser bliver ikke oversat til et protein, men virker som interne spacere mellem generne. Summen af mutationer over alle arveanlæg vil bevirke, at hvert nyt individ bærer på en eller flere nymutationer. De fleste nymutationer i strukturgenerne er skadelige, derfor sker der i hver generation en vis selektion på grund af lav fitness hos dyr, der er bære af de nye skadelige mutationer. Der vil over et stort antal generationer opstå en balance mellem nymutation og selektion.
For recessive arveanlæg kan ligevægtsgenfrekvensen (q) beregnes fra følgende ligning
q2*s = m,
hvor mutationsfrekvensen (m) er lig frekvensen af recessive individer, der bortselekteres i hver generation (q2*s).
For dominante arveanlæg kan ligevægtsgenfrekvensen (p) beregnes fra følgende ligning
(1/2)2pq*s = ps = m,
hvor mutationsfrekvensen (m) er lig med halvdelen af frekvensen af heterozygote individer, der bortselekteres i hver generation (pq*s) og q er approximativ 1. For definition af s se afsnit 3.2.
Migration sker i naturlige populationer oftest fra de nærmeste omgivelser. Derved får man jævne overgange i genfrekvens mellem de enkelte subpopulationer. I husdyravlen svarer migration til indkøb af avlsdyr, disse bliver normalt købt hvor de bedste dyr forefindes.
Naturlig selektion svarer til begrebet 'survival of the fittest' der er kendt fra Darwins udviklingslære. Den naturlige selektion vil sjældent nå til genfiksering, da en population i visse tilfælde pludseligt får ændrede milieuforhold. Derfor kan det være en fordel for populationen at bære på gener der ikke i den øjeblikkelige situation er de mest optimale. Når der er tale om recessive gener, kan disse bæres i lav frekvens med ringe tab af livskraft (fitness) til følge.
I forbindelse med nedsat fitness eller letalgener taler man om 'genetic
load' for populationen. Populationen taber de bortselekterede i hver generation
og en population er kun i stand til at bære en vis byrde, her spiller
nymutationerne dog kun en mindre rolle. Det er derimod en meget stor omkostning
at vedligeholde systemer, hvor der er overdominans med bortselektion af
begge de homozygote typer med en vis frekvens i hver generation.
Figur 3.2. Tyr af Belgisk Blåhvid race med dobbelt muskelhed. |
 |
I de næste afsnit vil der blive givet formler for hvorledes genfrekvensen
ændre sig, når der er lagt et selektionstryk på en bestemt
genotype. Formlerne er udviklet, så de både kan anvendes ved
naturlig såvel som menneskeskabt selektion på begge køn.
I husdyrpopulationer behandles de to køn vidt forskelligt, derfor
skal formlerne ofte anvendes på hvert køn for sig. Har man
f.eks. en situation hvor man kan DNA teste handyrene for en recessiv
nedarvet sygdom, og dermed sikre at alle avlshannerne er fri for sygdomsgenet.
Da vil man halvere frekvensen af sygdomsgenet i hver generation, da halvdelen
af generne kommer fra fædrene og halvdelen fra mødrene.
Ved selektion mod den recessive får man følgende opstilling. Selektion (s) mod den recessive skal opfattes relativt i forhold til de dominante typer. Lille s er den proportion af en given genotype, der bortselekteres i hver generation.
Ved selektion får man: --------- Genotype EE Ee ee Total Frekvens p2 2pq q2 = 1,00 Fitness 1 1 1-s Proportion p2 2pq q2(1-s) = 1-sq2 efter selektion ---------
Efter selektion beregnes genfrekvensen ved gentællemetoden, q' bestemmes som halvdelen af heterozygoterne plus de overlevende recessive relativ til halvdelen af proportionen efter selektion af alle overlevende gener, der er lig 1-sq2.
q' = (2pq/2 + q2(1-s))/(1-sq2)
| Figur 3.3. Selektion mod den recessive og ændring i genfrekvens over generationerne. Ved lave genfrekvenser er ændringerne meget langsomme. |
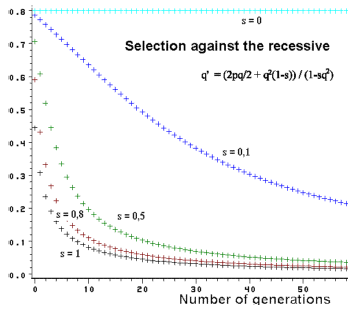 |
I figur 3.3 kan man se en sådan anvendelse. Ved stærk selektion, s=1, ændres genfrekvensen meget hurtigt ved høje genfrekvenser. Er genfrekvensen derimod lav, påvirkes frekvensen kun i ringe grad. Populationen parkerer genet i en slags venteposition. Dette er meget ubehageligt, såfremt det drejer sig om et sygdomsgen i en husdyrbestand. Man bliver aldrig helt af med det skadelige gen. Der er derfor stor interesse for at finde DNA testmetoder, hvorved man kan påvise heterozygote anlægsbærer.
Det fremgår endvidere, at ved et svagt selektionstryk er ændringerne i genfrekvensen altid meget langsomme.
Ved s=1 kan formlen for genfrekvens ændring udvides til at gælde n generationer og man har, når q0 er genfrekvensen i udgangspopulationen:
qn = q0/(1+n*q0)
n = 1/qn - 1/q0
n = 1/0,005 - 1/0,01 = 200 - 100 = 100
Applet til at beregne ændring i genfrekvens for forskellige fitness kombinationer, klik her, se nedenstående graf med eksempel på 1 generations selektion mod den recessive med fitness på 0,5.

DNA test og bortselektion af heterozygote handyr
For recessive sygdomme går der uendelig lang tid med at fjerne et sygdomsgen fra
en population, når man kun kan selektere mod den recessive. I mange populationer
er der relativt meget færre handyr end hundyr, derfor
kan det ofte betale sig kun at DNA teste handyrene. De bidrager med halvdelen
af generne til den nye generation, og man vil derfor kunne nedbringe frekvensen af sygdomsgenet
til halvdelen i hver generation, såfremt der kun avles med hannerne, der er fri for sygdomsgenet.
Man vil samtidig opnå, at der ikke sker nogen udspaltning af de recessive syge individer.
Eksempel: Hos SDM malkekvægracen forekommer den recessivt nedarvede
sygdom, BLAD (Bovin Leucocyte Adhesion Deficiency). I 1992 var man oppe på en genfrekvens
på 15 % i hundyr populationen af BLAD genet. Ved systematisk at
gennemføre 'BLAD DNA test' på de nye tyre er
frekvensen i 1999 langt under 10 %. Og frekvensen af BLAD-genet halveres
for hver ny generation.
Ved selektion for heterozygote (overdominans) får man følgende opstilling. Selektion mod den recessive (s2) og den dominante (s1) skal opfattes relativt i forhold til den heterozygote type.
Ved selektion får man: --------- Genotype EE Ee ee Total Frekvens p2 2pq q2 = 1,00 Fitness 1-s1 1 1-s2 Proportion p2(1-s1) 2pq q2(1-s2) = 1-p2s1 - q2s2 efter selektion ---------
Efter selektion beregnes genfrekvensen ved gentællemetoden, som vist i afsnit 3.2.
q' = (q2*(1-s2) + pq)/(1-p2s1 - q2s2)
delta q = q' - q = pq(ps1-qs2)/(1-p2s1 - q2s2) = 0
ps1-qs2 = 0
der løst giver m.h.t. q giver ligevægtsfrekvensen
q(hat) = s1 / (s1 + s2) eller
p(hat) = s2 / (s1 + s2)
Delta q er ændring af genfrekvensen fra en generation til den næste.
Når genfrekvensen er større end ligevægtsfrekvensen q(hat), får man et negativt delta
q, og er genfrekvensen mindre får man et positivt delta q.
Selektion for heterozygoter er derfor selektion uden ende. Det er derfor en kostbar
polymorfi at opretholde med et stort genetic load.
Overdominans udnyttes bedst i husdyravlen ved at producere
krydsningsdyr, hvor alle kan blive heterozygoter.
Figur 3.4.
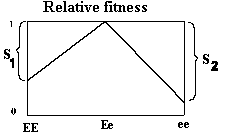 |
Eksempel: Fra den humane genetik er det klassiske eksempel på overdominans forekomst af
den Mendelsk recessiv nedarvede segelcelleanæmi med stor hyppighed (omkring 5% svarende
til q = 0,22) i malariaområder.
Individer der er heterozygotiske m.h.t
segelcelleanæmien er resistente mod malaria, hvilket giver dem en større overlevelses chance
end normale individer. Individer med anæmi har ringe overlevelseschancer s2=1.
Hvad er fitness for de homozygot normale i forhold til heterozygoterne ?
ligevægt opstår ved p(hat) = s2 / (s1 + s2) = 1 - q(hat) =1 - 0,22 der løst give s1 = (s2 /(1 - q(hat))) - s2 = 0,285
Applet til at beregne ændring i genfrekvens for forskellige fitness kombinationer, klik her
Ved selektion mod heterozygote kan man bruge samme opstilling som ved selektion for heterozygoter. Selektion (s) på den recessive og dominante, der nu er negativ, skal opfattes relativt i forhold til den heterozygote type.
Ved selektion får man: --------- Genotype EE Ee ee Total Frekvens p2 2pq q2 = 1,00 Fitness 1-s1 1 1-s2 Proportion p2(1-s1) 2pq q2(1-s2) = 1-p2s1 - q2s2 efter selektion ---------
Efter selektion beregnes genfrekvensen ved gentællemetoden, som vist i afsnit 3.2.
q' = (q2*(1-s2) + pq)/(1-p2s1 - q2s2)
Frekvensen q' repræsenterer de gener der overlever og vil således
svare til genfrekvensen i næste generation før selektion.
Der opstår ligevægt ved
delta q = pq(ps1-qs2)/(1-p2s1 - q2s2) = 0
q(hat) = s1 / (s1 + s2)
Figur 3.5.
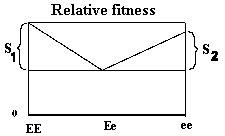 |
Man får, at når genfrekvensen q er større end ligevægts frekvensen q(hat) et positivt delta q, og når genfrekvensen er mindre, et negativt delta q. Selektion mod heterozygoter er derfor en ustabil situation. I visse tilfælde kan der være selektion mod de heterozygote i en livsperiode og selektion for dem i en anden, der kan derved alligevel opstå ligevægt.
Et eksempel på selektion mod heterozygoter har man ved kromosompolymorfien hos blåræve, der er vist i afsnit 10.3. De heterozygote individer har lavere reproduktionsevne end de homozygote individer, men polymorfien findes endog i de fleste naturlige populationer.
Der er problemer med
H-W ligevægten i den lille population, da et gen her kan ændre frekvens
på grund af tilfældigheder.
I den
mindst mulige populationsstørrelse med 1 han og 1 hun kan der kun bæres fire arveanlæg
videre til næste generation, hvilket i et to allel system med p=0,5
svarer til nedenstående fem mulige genfrekvenser, såfremt de to forældre er
heterozygoter:
AA x AA q=0 AA x Aa q=0,25 AA x aa q=0,5 Aa x Aa q=0,5 Aa x aa q=0,75 aa x aa q=1Er genfrekvensen 0 eller 1, siges genet at være tabt eller fikseret. Trækkes der fra en udgangspopulation med en genfrekvens på p =0,5 fire gener, er chancen for tab eller fiksering (alle fire gener er a eller alle er A) 0,54 = 0,0625.
Figur 3.6.
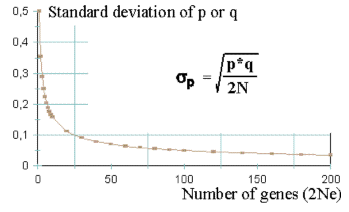 |
Ved ekstremt lave eller høje genfrekvenser har antal individer endnu større betydning for, om et gen går tabt eller fikseres. I den store population kan selv gener med meget lave frekvenser fastholdes. Som generel regel kan afledes af ovenstående figur, at en stor population tælles i hundrede og små populationer tælles i tiere.
Populationsstørrelse er problemet når man taler om truede dyrearter. Såfremt en art kommer under 100
avlsindivider vil den stort set kun kunne overleve såfremt der gøres en indsats for at forøge
den effektive populationsstørrelse, se lektion 9.3.
I den lille population vil såfremt den overlever ske meget hurtigere ændringer væk fra udgangspopulationen.
Darwin beskrev fænomenet som 'evolution by isolation', han baserede sin teori på iagttagelser på
de mange isolerede øer i Stillehavet. Her var dyrelivet meget forskelligt
fra dyrelivet på kontinenterne, og han konkluderede at her var evolutionen gået særligt
hurtigt på grund af isolationen.
Hver ny generation får halvdelen af generne fra fædrene og halvdelen fra mødrene.
Dette kan have stor betydning feks. i forbindelse med kvægavl, hvor der er mulighed
for kunstig sædoverføring. Antallet af køer er her meget stort i forhold til antallet af tyre.
Ved ulige fordeling af kønnene beregnes den effektive populationsstørrelse (Ne)
efter følgende formel:
4/Ne = 1/Nhanner + 1/Nhunner eller løst m.h.t Ne
Ne = (4Nhanner * Nhunner)/(Nhanner + Nhunner)
Eksempel 1) 10 hanner og 10 hunner
4/Ne = 1/10 + 1/10 svarer til Ne = 20
Eksempel 2) 1 han og 10 hunner
4/Ne = 1/1 + 1/10 svarer til Ne = 3,7
Eksempel 3) 100 hanner og 100000 hunner
4/Ne = 1/100 + 0 svarer til Ne = 400
Variansen på genfrekvensen i næste generation svarer til den, som det beregnede Ne angiver, se foregående side. Er der lige mange hanner og hunner (eksempel 1), er Ne blot lig med summen. Er der uendelig mange hunner i forhold til antallet af hanner, er Ne lig 4 gange antallet af hanner. Det er det køn der er færrest af, der afgør populationens effektive størrelse.
Effektiv populationsstørrelse og stigning i indavlsgrad.
Populationens effektive størrelse har betydning i forbindelse med akkumulering af indavl i
en population. Når der kun er få dyr i en population, vil alle dyrene efter nogle få
generationer være i familie med hinanden. Når forældre til et dyr er i
familie, opstår der indavl, se lektion 4. Indavl har mange uheldige virkninger,
stigning i indavlsgrad er omvendt proportional med populationens effektive størrelse
og man har:
delta F = 1/(2*Ne)
I en population med Ne = 20, er indavlsstigning i hver generation 2,5 %. bgcolor="#ffffff">
1. Indavl og slægtskab, definition
2. Slægtskab og indavl, beregningseksempel
3. Simple former for tæt indavl
4. Udspaltning af recessive ved indavl
5. Tabularmetoden til beregning af slægtskab og indavl
6. Opgaver
- Lyd og billed show (real player should be installed) eller Billed show
Næste lektion bgcolor="#ffffff">
Indavl er ofte et negativt ladet ord, der generelt anvendes for at
beskrive en situation hvor der ikke bliver tilført nyt blod. Indavl er
resultatet af avl mellem beslægtede individer. Ved indavl er der mulighed
for at den samme allel fra en fælles ane blive ført ned gennem generationerne
til et indavlet afkom. Sådanne alleler er af identiske oprindelse (eng.
identical by decent). Da indavl kan resultere i alleler der er identiske
på grund af afstamning vil indavl resultere i et overskud af homozygoter
relativt i forhold til forventningen ved tilfældig parring.
Slægtskab er synonymt med 'værende i familie med'. Slægtskab er normalt
et positivt ladet ord, som f.eks. Jeg er i familie med den og den. I denne
lektion bliver begreberne slægtskab og indavl kvantificeret.
-----
Indavl opstår ved sammenparring af beslægtede individer. Ved beslægtede individer forstås
individer, der tilbage i stamtavlen har fælles aner. Aner kan være forældre, bedsteforældre
oldeforældre etc. Slægtskab behøver ikke at gå det samme antal generationer bagud, f.eks.
to individer er beslægtede, selv om den enes bedstefar er den andens far.
Alle individer i en population har normalt fælles aner, der ligger 10 til 20 generationer tilbage,
men regnes alligevel for at være ubeslægtede da bidragene til slægtskab fra de fjerne aner er meget ringe.
I Figur 4 er vist et eksempel på konsekvensen af indavl ved helsøskendeparring,
nemlig at der opstår identisk homozygoti hos afkommet.
|
Figur 4.1. Eksempel på indavl ved helsøskendeparring. De mulige resultater for identisk homozygoti er vist i skema for individet X, de er elementerne i diagonalen. A1A1, A2A2,A3A3 og A4A4, alle øvrige af de 16 mulige kombinationer giver heterozygoti. Indavlsgraden for individ X er derfor F = 4/16. |
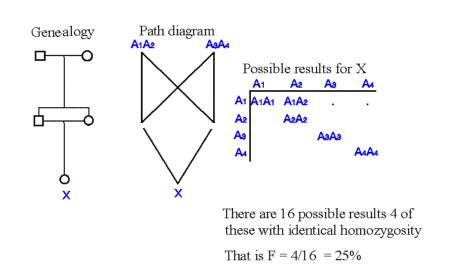
|
Et grafisk billede af indavl på kromosomniveau er vist her bgcolor="#ffffff">

Såfremt den eller de fælles aner er indavlede får man et ekstra bidrag til slægtskabet,
der kan ses af nedenstående endelige formel for additiv slægtskab,
idet n betegner antallet af generationer over
den fælles ane mellem individerne X og Y, og FA betegner indavlsgraden
for den fælles ane i den tilhørende sti. For eksempel i ovenstående eksempel, Figur 4.2,
er A og B de fælles aner begge med F=0.
Figur 4.3. Endelig formel for beregning af additiv slægtskabskoefficient mellem to dyr X og Y, og beregning af indavl på deres afkom Z. |
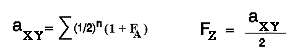 |
Større eksempel på beregning af indavl på grundlag af stamtavle. I nedenstående Figur 3 er vist en stamtavle med klassisk opstilling, hvert dyr er anført med dets to forældre bagud. Hvor f.eks. dyr nr. 18 har dyr nr. 17 som far og dyr nr.16 som mor. Der er endvidere vis et pilediagram, der er en slags reduceret stamtavle, hvor hvert dyr kun er anført en gang. Man går bagud i stamtavlen til de fælles aner for forældrene til dyr nr.18, og kun de stier der går bagud til en fælles ane medtages. Derefter findes de mulige forskellige veje fra dyr 17 til dyr 16 over en fælles ane. Vejene er anført i nedenstående tabel, Og indavls-koefficienten for dyr 18 er F18 = a17,16 /2 = 0,0606. Indavlskoefficienten for den fælles ane er 0 for dyr 1, 2 og 6, og 1/8 for dyr nummer 10 der er resultat af halvsøskendeparring.
Tabel over mulige veje (slægtskab) mellem dyr 16 og dyr 17 fra figur 3a.
Mulige veje Antal generationer (n) FA 1/2 i n'te 17 - 12 - 4 - 1 - 5 -10 - 14 - 16 7 F1=0 0,0078 17 - 12 - 4 - 2 - 5 -10 - 14 - 16 7 F2=0 0,0078 17 - 12 - 4 - 2 - 6 - 10 - 14 - 16 7 F2=0 0,0078 17 - 12 - 4 - 2 - 6 -11 - 15 - 16 7 F2=0 0,0078 17 - 13 - 10 - 5 - 2 - 6 - 11 - 15 - 16 8 F2=0 0,0039 17 - 13 - 10 - 6 - 11 - 15 - 16 6 F6=0 0,0156 17 - 13 - 10 - 14 - 16 4 F10=1/8 0,0704 sum = a17,16 0,1211
Figur 4.3a. Større eksempel på stamtavle og tilhørende pilediagram til beregning af slægtskabs og indavls-koefficienter. Hvert dyr er anført med dets to forældre bagud, hvor f.eks. dyr nr. 18 har dyr nr. 17 som far og dyr nr.16 som mor. |
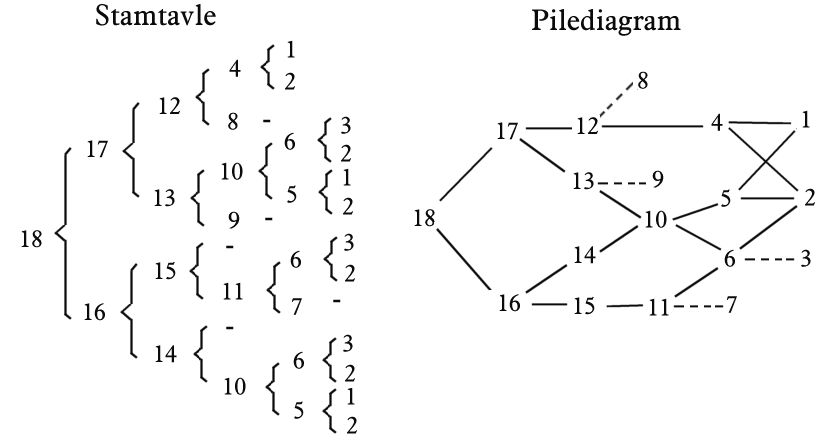 |
Figur 4.4. Slægtskab og indavl efter parring af tæt beslægtede individer.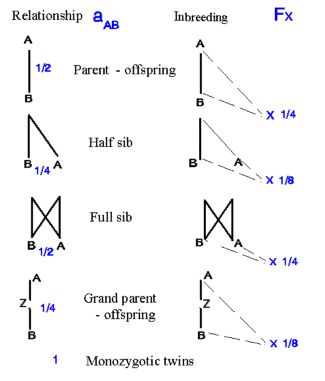 |
Indavlsgraden for afkommet er halvdelen af slægtskabsgraden mellem de to forældre. Hel og halvsøskende kan skaffes i stort tal indenfor husdyravl. Nye metoder for kloning af æg gør det også muligt at fremskaffe grupper af enægstvillinger.
Ved avl med laboratoriedyr feks. mus og rotter er det almindeligt at reproducere dyrene med fortsat helsøskendeparring. Lang de fleste stammer er 100 procent indavlede, og indavlen vedligeholdes med fortsat helsøskendeparring. Startes fra en udavlet population vil 20 generationers helsøskendeparring medføre, at indavlsgraden bliver på mere end 99 %. De fleste af vores husdyr har i øvrigt svært ved at reproducere sig ved indavlsgrader på mere end 50 %, idet indavl giver anledning til nedsat fitness, som vist i næste afsnit. bgcolor="#ffffff">
Ved indavl øges frekvensen af homozygot recessive individer i populationen, dette gælder især når genfrekvensen er lav.
Eksempel: I en population er genfrekvensen af et recessivt gen 0,01 svarende
til at frekvensen af homozygot-recessive individer er
0,0001 eller 1 per 10.000. Dannes en ny generation ved kun at anvende helsøskendeparringer,
får man en indavlsgrad på 25 % hos alle individer i næste generation.
I denne population er frekvensen af homozygot-recessive proportional med antallet af heterozygote
individer (2*0,01*0,99 = 0,0198) og deres chance for at der ved helsøskendeindavl, se figur 4.1,
sker udspaltning af den recessive (1/16),
der svarer til et af generne, sygdomsgenet.
Det kan enten være bedstefaderen eller bedstemoderen, der er bærere
af sygdomsgenet, derfor skal den samlede sandsynlighed
ganges med 2.
Den samlede sandsynlighed for homozygot-recessive individer er derfor 2*0,0198/16 = 0,0025,
hvilket er en forøgelse på 25 gange i forhold til den oprindelige udavlede population.
(Ved beregningerne er der ikke taget hensyn til de få tilfælde hvor andre kombinationer
af heterozygote
og homozygote er bedsteforældre, så resultatet afviger lidt i forhold til de nedenstående generelle formler),
indsættes i taleksemplet får man q2 + pqF =
0,0001 + 0,99*0,01*0,25 = 0,0026.
Det samlede antal homozygot-dominante vil tilsvarende blive forøget med samme proportion som de recessive på bekostning af de heterozygote individer, og man har under indavl i forhold til forventede antal under Hardy-Weinberg-ligevægt følgende forventninger, exp:
---------
Genotype AA Aa aa
Frekvens, exp p2 2pq q2
+pqF -2pqF +pqF
Disse forventede frekvenser kan give anledning til at
beregne indavlsgraden i subpopulationer;
som giver F = (H0 - Hn)/H0 ,
Beregning af indavl og slægtskab kan ske ved hjælp af tabularmetoden. Tabularmetoden har den fordel, at der ikke skal opstilles et diagram over dyrene, samtidig med at man hele tiden regner fremad. Man bygger altså videre på de foregående generationers indavl og slægtskab, da hvert trin kun går tilbage til forældrene.
Der anvendes kun to simple formler, idet slægtskab og indavl benævnes med a og F, som vist i efterfølgende 2 punkter.
1) Indavlen for et dyr (X) er lig med halvdelen af
slægtskabet mellem dets to forældre
A og B og det additive slægtskabet med sig selv er
aXX = 1 + FX
2) Additiv slægtskab mellem to dyr X og Y er lig
halvdelen af slægtskabet mellem det ældste dyr (X) og
det yngste dyrs (Y's) forældre A og B
aXY = (aXA + aXB)/2
Trin i opstilling af slægtskabs tabellen er vist nedenstående.
1) Skriv en linie med dyrnumrene (de ældste først)
2) Ovenover hvert dyrnr. skrives nummeret på hver af dets to forældre
3) Kopier trin 1) i en lodret søjle
4) Skriv en række 1'er i diagonalen
5) Beregn slægtskabet mellem dyr 1 og 2, 3, 4 op til n
6) Kopier først række i første søjle
7) Beregn slægtskabet mellem dyr 2 og 3, 4 op til n
8) Kopier anden række i anden søjle
9) etc. - - til diagonal elementet i hver række adderes halvdelen af forældrenes slægtskab
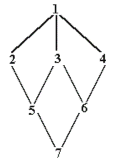 |
Dyr Far Mor 1 0 0 2 1 0 3 1 0 4 1 0 5 3 2 6 3 4 7 5 6
Forældre - 1 - 1 - 1 - 3-2 3-4 5-6
Dyr nr. 1 2 3 4 5 6 7
-----------------------------------------
1 1
2 1
3 1
4 1
5 1
6 1
7 1
skal indsættes er værdien for dyr 2. Man gå op i forældre rækken
her står 1 og - (ukendt). Værdien i kolonne 1 er 1 og ukendt sættes til 0
hvilket giver(1 +0)/2 = 1/2 der indsættes. Samme resultat får man for dyr
3 og 4. For dyr 5 er forældrene 2 og 3, i de tilsvarende
kolonner står der nu 1/2 og 1/2, der lægges sammen og deles med
to der giver en 1/2. Resultatet er det samme for dyrene
6 og 7. Herefter kopieres første række i første søjle og man har.
Forældre - 1 - 1 - 1 - 3-2 3-4 5-6
Dyr nr. 1 2 3 4 5 6 7
-----------------------------------------
1 1 1/2 1/2 1/2 1/2 1/2 1/2
2 1/2 1
3 1/2 1
4 1/2 1
5 1/2 1
6 1/2 1
7 1/2 1
Forældre - 1 - 1 - 1 - 3-2 3-4 5-6
Dyr nr. 1 2 3 4 5 6 7
-----------------------------------------
1 1 1/2 1/2 1/2 1/2 1/2 1/2
2 1/2 1 1/4 1/4 5/8 1/4 7/16
3 1/2 1/4 1
4 1/2 1/4 1
5 1/2 5/8 1
6 1/2 1/4 1
7 1/2 7/16 1
Forældre - 1 - 1 - 1 - 3-2 3-4 5-6
Dyr nr. 1 2 3 4 5 6 7
-----------------------------------------
1 1 1/2 1/2 1/2 1/2 1/2 1/2
2 1/2 1 1/4 1/4 5/8 1/4 7/16
3 1/2 1/4 1 1/4 5/8 5/8 5/8
4 1/2 1/4 1/4 1 1/4 5/8 7/16
5 1/2 5/8 5/8 1/4 1+1/8
6 1/2 1/4 5/8 5/8 1
7 1/2 7/16 5/8 7/16 1
Forældre - 1 - 1 - 1 - 3-2 3-4 5-6
Dyr nr. 1 2 3 4 5 6 7
-----------------------------------------
1 1 1/2 1/2 1/2 1/2 1/2 1/2
2 1/2 1 1/4 1/4 5/8 1/4 7/16
3 1/2 1/4 1 1/4 5/8 5/8 5/8
4 1/2 1/4 1/4 1 1/4 5/8 7/16
5 1/2 5/8 5/8 1/4 1+1/8 7/16 25/32
6 1/2 1/4 5/8 5/8 7/16 1+1/8 25/32
7 1/2 7/16 5/8 7/16 25/32 25/32 1+7/32
Tabularmetoden kan edb'ficeres på en meget simpel måde, så den metode er den foretrukne når beregningerne skal ske i store dyrebestande.
Pile diagrammerne anvendes bedst i forbindelse med genealogien, hvor det er vigtigt med overblikket. I sådanne tilfælde spiller det enkelte dyr ofte en betydelig rolle.
For at gennemføre beregningerne er det lettest at anvende et edb program, klik her for applet. Udskrift fra et DOS program, der kan analyserer hele populationer, kan ses her. Ønskes programmet taget hjem klik her og fejl liste filen klik her. Når din browser foreslår save, klik save tasten og gem filen som 'inbred.exe' og fl90.exe. Omdøb fl90.zip filen til fl90.eer. Filen inbred.exe der er en dos fil kan nu eksekveres under DOS. Input filen generes som vist i udskrifts eksemplet.
1. Formulering af genetiske hypoteser og genealogiske symboler
2. Autosomal recessiv arvegang
3. Autosomal dominant arvegang
4. Kønsbunden recessiv arvegang
5. Kønsbunden dominant arvegang
6. Testparringer, statistisk test
- Lyd og billed show (real player should be installed) eller Billed show
8. Opgaver
Næste lektion bgcolor="#ffffff">
Her er vist de mest anvendte genealogiske symboler og opstilling af genealogiske diagrammer.
Der kan formuleres en genetisk hypotese, som kan afprøves (be- eller afkræftes) v.h.a. statistiske metoder.
Der kan skelnes mellem autosomal recessiv arvegang, autosomal dominant arvegang, kønsbunden recessiv
arvegang og kønsbunden dominant arvegang. Ved undersøgelser af feltdata og/eller data fra testparringer kan
den enkelte hypotese indebære udspaltning som 1:1, 3:1 og 7:1, der hver kan afprøves med en statistisk test.
-------
Når der opstår nye egenskaber eller sygdomme, er det vigtigt, at der formuleres genetiske
hypoteser som alternativer til andre exogene årsagsforhold. Exogene faktorer kan være
fejlernæring, opstaldningsforhold, mikrobiel infektion eller evt en kombination af exogene og
endogene (genetiske) faktorer.
I de tilfælde, hvor der kan være tale om genetisk betingede sygdomme, er et af de
nødvendige
karakteristika en vis familievis optræden, og især at kun en vis del af et kuld (familie)
får lidelsen. De typiske Mendelske udspaltningsforhold er en 1:1, 1:3 og 1:7. I denne
sammenhæng vil der ikke blive omtalt egenskaber med intermediær nedarvning, da den
type egenskaber er meget sjældne i forbindelse med sygdomme.
Alternativer til Mendelsk udspaltning er de såkaldte tærskelsygdomme, hvor det er
summen af
milieu og genetiske faktorer, der udløser sygdommen. Tærskelsygdomme med lav frekvens vil
udvise familievis optræden, der minder meget om Mendelsk udspaltning,
se afsnit 8.3 vedr. tærskelegenskaber.
Der skal her endvidere erindres om den skematiske oversigt over
de forskellige nedarvningsformer givet i lektion 1.4.
Ved simpel Mendelsk arvegang kan der skelnes mellem 4 forskellige nedarvningsformer. Egenskaben kan nedarves dominant eller recessivt i forhold til normaltypen, og egenskaben kan udvise autosomal eller kønsbunden nedarvning. På de følgende sider vil de fire simple nedarvningsformer blive demonstreret. Det skal pointeres, at de nævnte indikationer på Mendelsk arvegang, kun kan anvendes såfremt populationsfrekvensen er lav, som det altid vil være tilfældet for nyopdukkede genetisk betingede sygdomme indenfor en eller nogle få familier.
| Figur 5.1. |
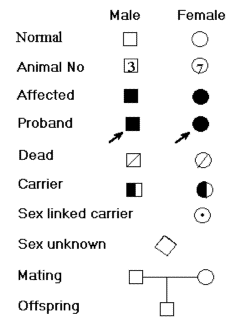 |
Er der tale om sygdomme med høj populationsfrekvens som f.eks. brystkræft i den humane population, vil der ofte være tale om en betydelig heterogenitet. Denne sygdom har en genetisk baggrund, der kan skyldes udspaltning af gener på flere forskellige uafhængige loci. Så det er svært at sammenligne udspaltningen mellem familier, men analyse kan fortsat foregå indenfor en stor familie. Endelig er der problemet med fænokopier, dvs at en identisk sygdom er forårsaget af ikke genetiske årsager.
De forskellige symboler der anvendes indenfor genealogi er vist i figur 5.1.
Proband individet er det individ der har givet anledning til undersøgelsen. Dette individ eller familien skal normalt udelukkes ved evt. senere statistisk undersøgelse. Ved siden af det egentlige genealogiske diagram kan der dog også anvendes en kombination af pilediagrammer og genealogiske diagrammer. bgcolor="#ffffff">
Faktorer der indicerer autosomal recessiv arvegang.
Se nedenstående eksempel, figur 5.2.
Figur 5.2. 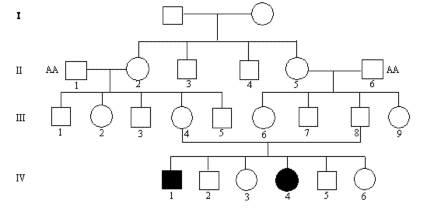
Typiske eksempler på recessiv nedarvning er gener der koder for enzymer, da et normalt gen almindeligvis er tilstrækkeligt til at individet fungerer normalt. Der kan normalt kompenseres ved øget transkriptions aktivitet.
Se i øvrigt eksempel på recessiv udspaltning her bgcolor="#ffffff">
Faktorer der indicerer autosomal dominant arvegang.
Se nedenstående eksempel, figur 5.3.
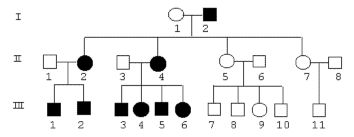
Typiske eksempler på dominant nedarvning er gener der koder for membranproteiner, byggesten i væv etc.. bgcolor="#ffffff">
Det er forudsat, at det drejer sig om pattedyr, hvor kønskromosomerne benævnes XX og XY hos henholdsvis hunner og hanner. Når det drejer sig om fugle, er det hunnen der er heterogametisk, så argumenterne må for fugle vendes om i forhold til køn.
Faktorer der indicerer kønsbunden recessiv arvegang.
I Figur 5.4 er vist røntgenbillede af Svensk Dansk gårdhund afficeret med spondylo-epifysal dysplasia. Billederne er taget på Røntgen-Klinikken her ved KVL af J. Arenbjerg. Lidelsen er sandsynligvis kønsbunden recessiv.
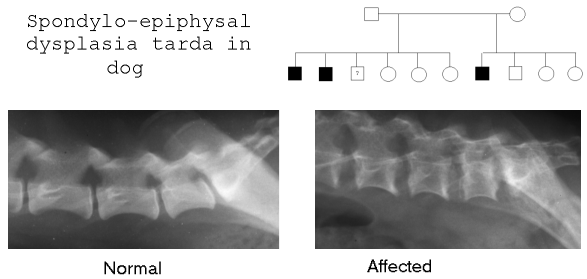
Det er forudsat, at det drejer sig om pattedyr, hvor kønskromosomerne benævnes XX og XY hos henholdsvis hunner og hanner. Når det drejer sig om fugle, er det hunnen der er heterogametisk, så argumenterne må for fugle vendes om i forhold til køn.
Faktorer der indicerer kønsbunden dominant arvegang.
Se nedenstående eksempel, figur 5.5.
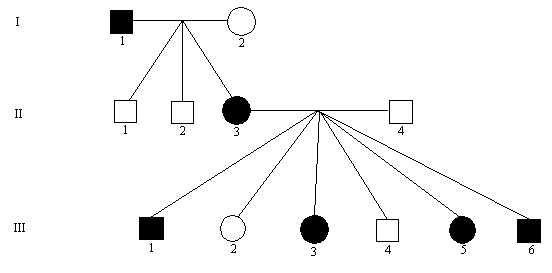
Når der foreligger et mindre materiale, der tyder på Mendelsk udspaltning, vil der ofte være alternative hypoteser, som ikke kan udelukkes. Der kan jo tillige være simuleret genetik (fænokopier) eller nedarvning som en tærskelegenskab, hvor udspaltningen (forekomsten) kan minde om simpel Mendelsk nedarvning. I sådanne tilfælde må der gennemføres testparringer for at få sagen endelig klarlagt.
Testparringer kan i mange tilfælde blot være afventning af fødsler, hvor man i forvejen kan forudsige resultatet, såfremt en given hypotese kan fastholdes. Afviger resultatet, må der formuleres en ny hypotese, der kan afprøves.
Et af de vigtige spørgsmål man må stille sig, før der gennemføres egentlige testparringer, er hvor stort et datamateriale er nødvendigt, for at en given test kan give et tilfredsstillende endegyldigt svar.
Testparring af tyr, der er mistænkt anlægsbærer, kan ske ved at parre tyren med køer, der har lidelsen, med kendte anlægsbærere eller med egne døtre. Hvor mange stk. raskt afkom skal tyren have før han kan frikendes som anlægsbærer i de tre tilfælde. Sandsynlighederne for at der fødes normalt afkom i de tre tilfælde er henholdsvis ˝, 3/4 og 7/8. Ved anvendelse af sandsynlighedsregningens multiplikationsregel har man for en parring med kendte bærere, at sandsynligheden for at få n normale afkom er (3/4)n. Ved hjælp af denne formel og signifikansgrænserne 0,05, 0,01 og 0,001 kan n bestemmes, således at de klassiske sandsynlighedskriterier kan opfyldes.
Antal afkom (n) der er nødvendig for at udelukke at en tyr er anlægsbærere
Udelukkelse af at Sandsynlighed Formel være bærere ved test ------------------------------ parring af tyr til 0,05 0,01 0,001 (x)n mindre end Kendte recessive 5 7 10 x=1/2 Kendte anlægsbærere 11 16 24 x=3/4 Egne døtre 23 35 52 x=7/8
Sandsynligheden 7/8 for normalt afkom efter heterozygotisk individ ved fader datter parringer kan afledes af figur 5.6. Antallet af afkom der skal anvendes for at frikende faderen for at være anlægsbærer på 5% niveauet er (7/8)n = 0,05 svarende til n*ln(7/8) = ln(0,05), der afrundet giver n=23.
Figur 5.6. 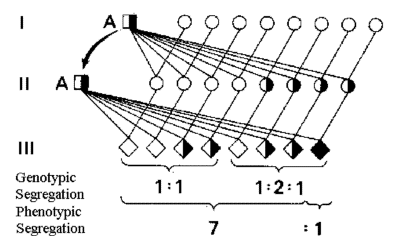
Parring med egne døtre har tillige den fordel, at det tester faderen for alle mulige andre recessive arveanlæg, end det som den er under mistanke for.
Ved test af udspaltningsforhold for kendte parringer kan der anvendes Chi-i-anden test. Testen minder ved parring af kendte anlægsbærere om testen for H-W udspaltning, men nu er det forventede blot i forholdet 1:2:1 ved codominans eller 3:1 ved dominans. De forventede antal fås ved at multiplicere forventet frekvens med N.
Udspaltning ved testparring Aa x Aa, codominant nedarvning.
--------- Genotype AA Aa aa Total Antal, obs 30 51 39 = 120 = N Frekvens, exp 1/4 ˝ 1/4 = 1,00 Antal, exp 30 60 30 = 120 Afvigelse 0 -9 9 Chi-i-anden 0 1,35 2,70 = 4,05 ----------
Df = 3-1 = 2, da materialet kun leverer parameteren N til beregning af forventet antal. Chi-i-anden værdien er mindre end H0 testværdien 5,99, så der er ikke signifikant afvigelse fra en 1:2:1 udspaltning på 5% niveauet.
Udspaltning ved testparring Aa x Aa, dominant nedarvning
--------- Genotype AA+ Aa aa Total Antal, obs 81 39 = 120 = N Frekvens, exp 3/4 1/4 = 1,00 Antal, exp 90 30 = 120 Afvigelse -9 9 Chi-i-anden 1,00 2,70 = 3,70 ----------
Df = 2-1 = 1, da materialet kun leverer parameteren N til beregning af forventet antal. Chi-i-anden værdien er lige under H0 testværdien 3,84, så der er ikke signifikant afvigelse fra en 3:1 udspaltning på 5% niveauet.
Applet til beregning af Chi-i-anden for Mendelske udspaltninger ved testparringer, klik her. bgcolor="#ffffff">
Når der arbejdes med feltdata, og når det drejer sig om nye sygdomme, er det nødvendigt at arbejde med familier, hvori sygdommen optræder. Når man på grundlag af sådanne observationer vil beregne om udspaltningen stemmer overens med Mendelsk arvegang, er det nødvendigt at korrigere for de familier der kunne spalte ud, men på grund af tilfældigheder ikke gør det.
| Figur 5.7 |
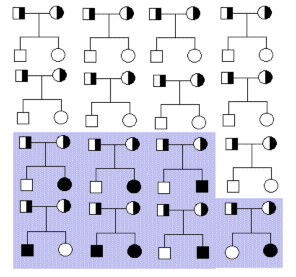 |
Er der tale om recessiv arvegang og man har en familie, hvor begge forældre er heterozygote, vil der være 3/4 chance for at familien ikke bliver afsløret på grund af sygt afkom, efter det første afkom er født. Efter andet afkoms fødsel vil chancen være (3/4)2 = 9/16. I nedenstående figur er vist, hvorledes heterozygote forældre vil spalte ud i en familiestørrelse på to. I de 9 ud af 16 familier vil der ikke være afficeret afkom, så når de ikke medtages i den endelige analyse, bliver den klassiske Mendelske analyse meningsløs.
I det følgende er vist formler for test og beregning af korrigeret udspaltningsforhold fra familier med udspaltning. Relevante data (skraveret område) fra figur 5.8 er derfor:
T = 14 -total antal A = 8 -antal afficerede A1 = 6 -antal familier med 1 syg A2 = 1 -antal familier med 2 syge
I figur 5.8 er vist et pilediagram over minkfamilier fra en farm, hvor der har været et stort udbrud af tyrosinæmi. Et af de kliniske symptomer er som vist på billedet, at øjenlågene klistrer sammen. Hvalpene dør efter en til to dages sygdom, tilfældene optræder ved en alder af ca 6 uger. En detaljeret beskrivelse af sygdommen foreligger i Christensen et al. Canadian J. Comparative Medicine, 43:333-340, 1979.
Figur 5.8. Udspaltning af tyrosinæmi i en minkbestand (fyldte symboler),
billedet til højre viser en angrebet minkhvalp med de typiske tilklistrede øjne.
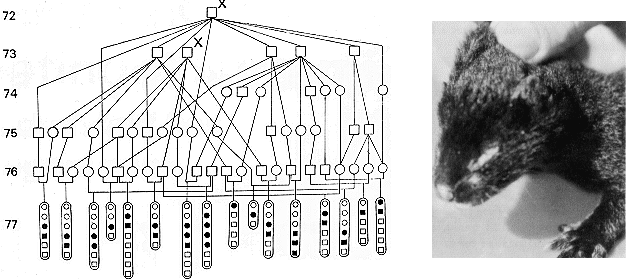
De formler der skal anvendes ifølge "Singles metode" for test om Mendelsk
nedarvning (for proportionen p-hat) er vist i nedenstående figur.
Der er tillige anført tal fra ovenanførte mink tyrosinæmi tilfælde
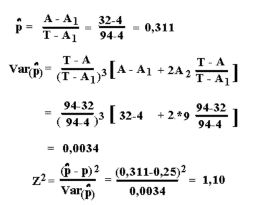
I ovenstående mink familie findes ved optælling at:
T = 94 -total antal hvalpe A = 32 -antal afficerede A1 = 4 -antal familier med 1 syg A2 = 9 -antal familier med 2 syge
Beregningerne er anført i ovenstående figur. Der er ikke signifikant afvigelse fra en 3 til 1 udspaltning da testværdien er mindre end 3,84 (H0: p(hat) = p =0,25). Bemærk endvidere at familier med mere end 2 syge ikke direkte indgår i beregningerne, men kun bidrager til totalt antal afficerede. En applet til brug ved beregningerne kan kaldes her
Indsættes tallene fra det første teoretiske eksempel (Fig. 5.7) i formlen for p(hat) får man (8-6)/(14-6) = 0,25, hvilket naturligvis er det korrekte resultat, idet data stammer fra parring af kendte heterozygoter.
1. Definition af kvantitativ egenskab samt fænotype og genotype
2. Begreberne genotypeværdi, avlsværdi og dominansafvigelse
3. Begreberne additiv varians og heritabilitet
4. Estimering af heritabilitet og fælles milieu faktor
5. Opgaver
- Lyd og billed show (real player should be installed) eller Billed show
Kvantitative egenskaber er karakteriseret ved at være påvirket af effekten
af alleler i mange loci og af milieu påvirkninger. Alleler som påvirker
kvantitative egenskaber, kan identificeres ved hjælp af genetisk kortlægning
med DNA markører, eller ved kendskab til kandidatgener på grundlag af basal
fysiologi og udvikling af egenskaben. Avlsværdi er den del af genotypeværdien
der kan genfindes hos afkom. Det relative bidrag af genotypen og af milieuet
kan måles via det relative bidrag til den totale varians fra den additive
genetiske (avlsværdi) varians og milieu variansen. Additiv genetisk varians
kan feks. bestemmes via beregning af forældre-afkom korrelation, og milieu
variansen måles som en rest. Heritabiliteten bestemmes som en ratio mellem den
additive varians og den phenotypiske (totale) varians. Heritabiliteten kan anvendes
til at forudsige resultatet af et selektionsprogram, eller ved estimering af
avlsværdi.
------
I første lektion blev givet en definition på begreberne fænotype og genotype for en kvantitativ egenskab ud fra nedenstående
ligning. Begreberne er indtil nu kun anvendt på kvalitative egenskaber.
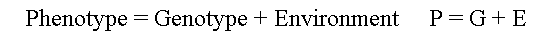
Fordelingen af fedtprocent er karakteriseret ved en middelværdi og en spredning. For SDM (Sortbroget Dansk Malkerace)
er middelværdien 4,3 procent og spredningen er 0,25 procent enheder. Dvs. at de fleste køer har fedt procenter omkring 4,3,
og kun meget få har fedtprocenter på 3,5 eller 5,0. For Jersey racen derimod er middelværdien 6,4 procent.
Et dyrs præstation vil altid skulle bedømmes ud fra populationens middelværdi. F.eks vil en Jersey ko skulle måles ud fra
Jerseys middelværdi og ikke i forhold til SDM's.
Ved de kvantitative egenskaber er det almindeligvis sådan, at de er påvirket af effekten af mange genpar, så taler man om polygenisk nedarvning i modsætning til (monogenisk) enkelt-gen-nedarvning, der har været omtalt i de foregående kapitler.
Et dyrs phenotypeværdi (P) kan måles og vurderes i forhold til populationens middelværdi.
Et dyrs genotypeværdi (G) er phenotypemiddelværdi af individer med samme genotype.
| Figur 6.1. Svarer til definitionen af avlsværdi. En han får uendelig mange afkom, der indbyrdes er halvsøskende. |
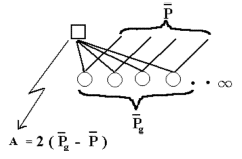 |
Et dyrs avlsværdi (A) er defineret på grundlag af dets afkom som to gange afkommets middelværdis afvigelse fra populationens middelværdi, når der er tilfældig parring. Dvs. afkommet er halvsøskende, se figur 6.1.
Populationsgennemsnittet kan adderes for at bringe avlsværdierne
op på normal skala.
Eksmpel: En Jersey tyr har 1000 stk. afkom hvis gns. ydelse er 4500 kg. mælk.
Populationsgennemsnittet er 4200 kg mælk. Tyrens avlsværdi er 2(4500-4200) + 4200 = 4800 kg. mælk.
Definitionerne gælder både når det drejer sig om en specifik
egenskab som kf. mælk, og når det drejer sig om effekt af gener på et enkelt
locus.
De til definitionerne svarende formler, når definitionen anvendes
på et enkelt locus, er vist nedenstående. Det er
forudsat, at der er en effekt af locus A på den egenskab der måles,
og gennemsnittet for dyr med de tre tilsvarende
genotyper er forskellige. Populationsgennemsnittet beregnes derefter som en
middelværdi, der beregnes som summen af genotyperneværdierne gange
genotypefrekvenserne, se eksempel med vægt hos mus figur 6.2.
| Figur 6.2. Definitionen af avlsværdi for genotypen A1A1 og regneeksempel. En hanmus med genotypen får uendelig mange afkom, der indbyrdes er halvsøskende. |
 |
Middelværdien af en population eller af A1A1's afkom beregnes som:
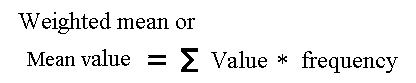
I ovenstående eksempel med musevægte er vist beregning af populationsmiddelværdi (P streg) og avslværdi for genotypen A1A1. En tilsvarende avlsværdi kan beregnes for genotypen A2A2, der ved tilfældig parring kan få afkom af typerne A1A2 og A2A2 med frekvenserne p og q. Avlsværdien for A2A2 bliver derfor 2(12*0,3+6*0,7 - 9,24) = -4,88.
Avlsværdien for heterozygoten bliver gennemsnittet af de to rene genotyper, da halvdelen af dens gameter er af typen A1 og den anden halvdel er A2. Avlsværdierne kaldes ofte additiv værdi, fordi de er proportionale med antallet af A1 gener i genotypen.
Såfremt der er en mere eller mindre udtalt dominans, vil genotypeværdien (G), den gennemsnitlige værdi af en bestemt
genotype, ikke være lig med avlsværdien (A), men der vil være en rest der skyldes dominansavigelser (D).
Graden af dominans afgøres ved at se på den heterozygote type i forhold til de to homozygote typer.
Eksempel på beregning af avlsværdi (A) og dominansafvigelse (D)
Genotype TT Tt tt ----------------------------------------------------------- Kg Mælk 1882 1882 2082 (Genotype)frekvens p2=0,45 2pq=0,44 q2=0,11 Og middelvædi = 0,45*1882 + 0,44*1882 + 0,11*2082 = 1904 kg
Avlsværdierne beregnes som vist nedenstående, idet der arbejdes med afvigelser fra populationsgennemsnittet, se skala:
TT og Tt Middelværdi tt
1882 1904 2082 Oprindelig skala
---|------|---------------------------|--> Genotype skala, kg
-22 0 178 Målt som afvigelse fra gns.
Genotype Avlsværdi
--------------------------------------------------
TT p Tt q
TT 2*[(-22*0,67 + -22*0,33) - 0] = -44
Tt = 22,6 ,middelværdi af de to homozygote
tt 2*[(-22*0,67 + 178*0,33) - 0] = 89,2
--------------------------------------------------
Genotypeværdierne er bestemt som afvigelse fra populationsgennemsnittet (se ovenstående skala), og avlsværdierne er beregnet som vist i henhold til definitionen. Herefter bestemmes dominansafvigelsen (D) som en rest, som vist i nedenstående opstilling.
Genotype G = A + D ------------------------------------- TT -22 = -44 + 22 Tt -22 = 22,6 + -44,6 tt 178 = 89,2 + 88,8 -------------------------------------
Resultater fra applet på muse examplet vist i Figur 6.2
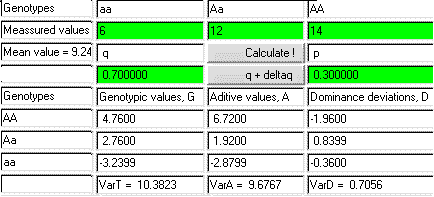 |
For et locus kan der beregnes varians der skyldes forskelle i avlsværdi eller i dominansafvigelser. Varians beregnes som en middelvædi af afvigelsernes kvadrat, så feks VA = (-44-0)2*0.45 + (22,6-0)2*0,44 + (89,2-0)2*0,11 = 1926, som i dette tilfælde er de kvadrede avlsværdier, taget fra ovenstående tabel, multipliceret med genotypefrekvenserne. Avlsværdiernes middelværdi beregnes som -44*0.45 + 22,6*0,44 + 89,2*0,11 = 0
En applet til beregninger af G, A og D findes her
Forsøg til bestemmelse af kvantitative geneffekter er omtalt nærmere i lektion 12.
Loci med indflydelse på en kvantitativ egenskab kaldes ofte QTL'er (quantitative trait loci).
Når der tales om additiv varians refererer det til varians på avlsværdierne (VA). (I senere lektioner anvendes ofte symbolet sigma2 som synonym for varians.) I det foregående er der vist, hvorledes avlsværdi kan beregnes for de enkelte genotyper i et locus. Når værdierne er kendte, kan der også beregnes en varians på avlsværdierne i dette locus. Såfremt der er uafhængighed mellem de enkelte loci, der har additiv effekt på en egenskab, bliver den samlede additive varians summen af varianser fra de enkelte loci. Den samlede additive varians kan ikke umiddelbart beregnes for individer i en population, idet avlsværdien for de enkelte individer ikke er kendt.
Den phenotypiske varians (VP) derimod beregnes på grundlag af målinger på de enkelte individer.
Heritabiliteten (h2) eller arvelighedsgrad for en egenskab er defineret som VA/VP. Heritabiliteten varierer derfor mellem 0 og 1, idet den additive varians er en del af den phenotypiske varians.
Beregning af heritabilitet kan ske på grundlag af lighed mellem beslægtede individer, målt som korrelation eller som regression, f.eks. regression af afkom på en af forældrene. Og der gælder følgende relation. Heritabiliteten kan beregnes som forholdet mellem den beregnede korrelation og slægtskabskoefficienten. Dvs. den maksimale korrelation mellem forældre og afkom er på en halv. Såfremt den er højere, må der være andre end genetiske årsager til at forældre og børn ligner hinanden. Den teoretiske baggrund for den forventede additive kovarians mellem beslægtede individer kan udledes efter lignende ræsonnementer som for den additive varians, idet man først beregner kovariansen i et enkelt locus og derefter summerer over alle loci.
Den bedste metode til beregning af heritabilitet er korrelation mellem halvsøskende, da de normalt kun har gener til fælles. Helsøskende derimod har ofte et maternelt milieu fælles, hvilket i så fald fører til overestimering af heritabiliteten. I praksis bruges sjældent forældre-afkom beregning af korrelation, da man så nødvendigvis skal skaffe data, der stammer fra to generationer. Der er endvidere problemer med at forældre og afkom ikke lever under de samme milieuvilkår, eller evt. at forældre og afkom deler fælles milieu.
En estimering af variansandelen, der skyldes fælles milieu, kan ske ved at sammenligne korrelation beregnet på grundlag af halv- og helsøskende. Forventningen er, at korrelation mellem helsøskende skal være dobbelt så stor som korrelation mellem halvsøskende. Det faktum, at den er større end to gange halvsøskende korrelationen, kan tilskrives fælles milieu for helsøskende. Denne komponent får betegnelsen (c2), hvor c står for 'common environment'. Den relative phenotypiske varians består af en genetisk del (h2) fælles milieu variansen (c2). Den resterende del af variansen skyldes tilfældige milieupåvirkninger, og den andel får betegnelsen (e2). For de fleste egenskaber udgør milieuvariansen den største del af den phenotypiske varians.
Tabel over de definerede genetiske parametre og deres symboler Additiv varians VA Phenotypiske varians VP Heritabiliteten h2 Fælles milieu c2 Tilfældig milieu e2 Halvsøskende korrelation (1/4)h2
| Figur 6.3.
Selektionsresultatet (R) er lig heritabiliteten gange selektionsdifferensen (S) Ændringen ses hos afkommet |
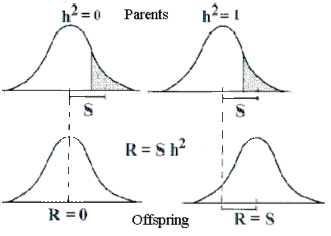
|
Historisk set har heritabiliteten en fortolkning mere. Såfremt der sker selektion, så de udvalgte avlsdyr (skraveret område i figur 6.3) afviger fra populationsgennemsnittet, vil gennemsnittet i næste generation ændres. Ændringen er proportional med selektionen og heritabiliteten og man har følgende formel:
R = h2*S
Selektions-resultatet eller -respons (R) er lig heritabiliteten gange selektionsdifferensen (S). Heritabiliteten er nul, såfremt egenskaben forbliver konstant ved selektion, og den er 1, såfremt ændringen er lige så stor som selektionsdifferensen, se figuren til højre og lektion 1 med ændring af fedtprocenten i mælken hos Dansk Jersey kvæg på grundlag af selektion.
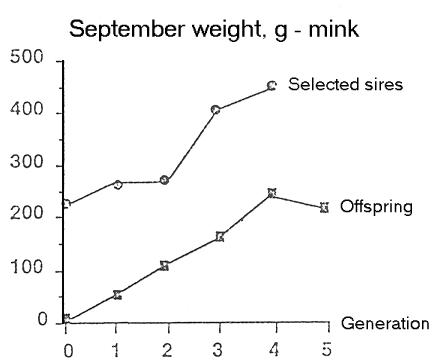
Figur 6.4. Eksempel på selektionsforsøg der danner basis for beregning af heritabilitet. |
R = h2*S kan også opfattes som regression af afkom på gennemsnittet af de to forældre, hvor regressionskoefficienten b er svarer til h2.
Heritabilitets estimering p.g.a. en beregnet korrelation.
Selektionsforsøget til bestemmelse af heritabiliteten tager lang tid, i det mindste
adskillige generationer. Nu vil
der nu blive præsenteret metoder til bestemmelse af heritabiliteten på grundlag af
data fra kun en generation.
Heritabilitet (h2) kan bestemmes som den beregnede korrelation (r eller t) mellem beslægtede individer i forhold til
slægtskabsgraden (a). Dette gælder såfremt
arv er den eneste årsag til lighed mellem de pågældende individer
og der ikke er indavl. Formel med symboler er følgende:
h2 = r/a, eller r = a*h2.
Korrelationsberegning kan ske efter klassiske statistiske beregningsmetoder (Figur 6.5), eller hvor der er flere ligestillede individer som f.eks, en gruppe halvsøskende ved hjælp af variansanalyse og den dertilhørende intraklassekorrelation.
| Figur 6.5. Eksempel på todimensional fordeling til beregning af korrelation, typisk egenskab hos mor og afkom eller mellem hel eller halvsøskende. 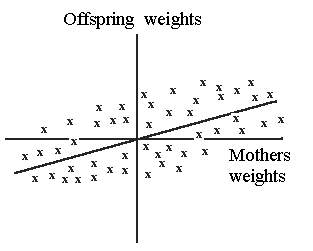 |
Beregning af heritabilitet kan ske både på grund af hel- og halvsøskendemateriale som, feks. findes hos alle multipare dyr. Heritabiliteten er et udtryk for, hvor meget dyrene ligner hinanden på grundlag af at de bærer fælles arveanlæg.
Hos f.eks. helsøskende er der som tillige nævnt ofte milieumæssige årsager til lighed. Det er især i de første levemåneder, hvor hvert kuld har sit eget specifikke milieu, idet moderen og dens moderegenskaber er en vigtig faktor for kuldets trivsel. Symbolet for denne komponent til lighed mellem beslægtede individer er som nævnt i foregående afsnit c2. Halvsøskende, der har fælles far, har normalt kun genetiske årsager til lighed.
Den generelle formel for fortolkning af korrelation mellem beslægtede individer bliver, idet der som symbol for denne korrelation anvendes t:
t = a*h2 + c2
Heritabiliteten beregnes nu på grundlag af halvsøskendekorrelationen, hvor c2 er 0, derefter beregnes c2 på grundlag af helsøskendekorrelationen.
Eksempel. Minkvægt ved 8 ugers alder, i alt 508 dyr fordelt på
107 kuld med 37 fædre.
Ved en statistisk analyse af vægtene for de 508 minkhvalpe blev
fundet. Halvsøskendekorrelation t = 0,03 og
helsøskendekorrelation t = 0,41.
Indsættes disse resultater i den genetiske model får man:
Halvsøskendekorrelation t = (1/4)*h2 + 0 = 0,03 svarende til h2 = 0,12.
Ved den meget unge alder er der en meget lav heritabilitet for vækst, hvorimod de maternelle faktorer spiller en stor rolle. For at se de statistiske beregninger på mink vægt estimaterne klik her.
Materiale til beregning af heritabilitet af højde hos mennesker er vist i lektion 1.
Heritabiliten blev som nævnt i lektion 1 beregnet som regressionen af
afkom på gennemsnittet af begge forældre. Den er for højde hos mennesker ca. 0,6.
Korrelationen mor-afkom er fundet til 0,4 mens korrelationen far-afkom kun har
en størrelse på 0,2. Forholdet med en lavere korrelation mellem far og afkom end mellem
mor og afkom må tilskrives at der er et betydeligt fælles milieu mellem mor og afkom.
For at se data og det anvendte SAS program for 2000 materiale klik her. Vil du køre din egen analyse overfør program og data via clip board til SAS, Dette gøres ved at trække musen hen over både program og data for at definere en blok. Når du har defineret blokken, gå op i edit feltet og gå til copy; når du har åbnet SAS bruges paste i edit feltet.
Her er et par små eksempler på anvendelse af variansanalyse til beregning af gentagelseskoefficient for minkkuld og heritabilitet for kroplængde hos svin. Programmerne hentes til SAS for minkmateriale klik her og for grisemateriale klik her Brug clip board som forklaret ovenfor.
Endelig er der et meget stort dataset fra grise med flere målinger (dgl. tilvækst, foderforbrug og kødprocent) fordelt på hel- og halv-søskendegrupper klik her
1. Avlsværdiskøn beregning, generel
2. Formler for beregning af avlsværdiskøn under ensartede slægtskab
3. Direct updating of breeding values, ikke pensum
4. Avlsværdiskøn generel, herunder brug af genmarkører
- Lyd og billed show (real player should be installed) eller Billed show
5. Opgaver
Forventningen til præstationen for en given egenskab er støre når man er
i familie med individer, der har en høj præstation (phenotype=P).
Jo tættere slægtskab jo højere forventning. I Figur 7.1 er angivet en formel,
der kan kvantificerer forventningen i et avlsværdiindeks (I) i en lang række
tilfælde med ensartede slægtskabsforhold. I Tabel i afsnit 7.2 er givet en del
eksempler på anvendelse af formelen. Tabellen omfatter feks. avlsværdiindeks bestemt
pga. præstationer fra egen, forældre, afkom, eller hel- eller halvsøskende, hvor
formlen anvendes til at beregne et avlsværdiindeks og dets sikkerhed.
Avlsværdiindekset kan blive lidt sikre bestemt ved anvendelse af metoderne,
der er omtalt i kapitel 12, da de medtager alle slægtninge.
-------
I en stor population med tilfældig parring skal hvert individ i gennemsnit have to stk. afkom, for at populationen er i balance
med hensyn til størrelse. Fordelingen af antal afkom i en sådan population har en venstreskæv binominalfordeling
(Poissonfordelt) med middelværdi 2 og varians 2. Dvs. at antal afkom per individer kan variere fra 0 og opefter med flest,
der har værdierne 0,1,2,3,4 og 5. I en sådan population kan der ikke på nogen måde bestemmes den eksakte avlsværdi for et
individ på grund af det lave antal afkom, man må nøjes med et avlsværdiskøn.
Et avlsværdiskøn betegnes ofte som et avlsværdiindeks (I). Indekset kan fremskaffes på grundlag af informationer om phenotypeværdier fra alle mulige slægtninge, hvor der kan anvendes enten en simpel regressionslinie eller multipel regression. Jo flere slægtninge der måles, desto sikrere vil skønnet blive. Korrelationen mellem sand avlsværdi (A) og indekset benævnes 'sikkerheden' og får symbolet rAI.
I figur 7.1 er vist, hvorledes der er sammenhæng mellem
phenotypemålinger og et avlsværdiindeks (I), der er et skøn for
den sande avlsværdi (A). Der er
tillige vist betydning af sikkerheden (rAI), idet sikkerheden
kvadreret på indekset giver
sig udtryk ved en reduceret varians på avlsværdiskønnet.
Alle værdierne er fortolket ud fra den klassiske regressionsligning hvor:
P'er = phenotypemålingerne
n = antal målinger,
Pg streg = gennemsnit af P'er,
a' = slægtskabsgrad mellem de målte dyr og det dyr der beregnes indeks for
a = slægtskabsgrad mellem de målte dyr (P'er)
P streg = Populationens gennemsnit
A streg = Populationens gennemsnitlige avlsværdier = lig P streg
h2 = heritabiliteten
c2 = fælles milieufaktor for de målte dyr
t = a h2 + c2
| Figur 7.1. Beregning af avlsværdi indeks på grundlag af regression på phenotype målinger. Definition af de enkelte parametre, se ovenstående. Eksempel på anvendelse af formlerne er givet i Figur 7.2. |
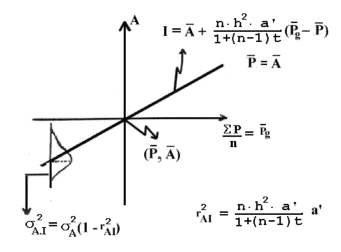 |
Avlsværdi indekset er baseret på teori omkring lineær regression og korrelation, basisdefinition
på disse begreber kan ses her.
Et eksempel på anvendelse af formlerne i Figur 7.1 er givet i
Figur 7.2, der er i næste afsnit tillige givet en
tabel over de mest almindelige tilfælde på avlsværdi indeks.
| Figur 7.2.
Eksempel på beregning af avlsværdi indeks for mælkeydelse for tyr på grundlag af målinger på 20 stk. havlsøskende afkom. |
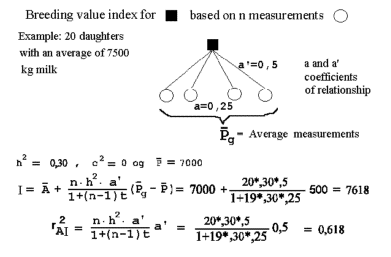 |
Her er vist et genealogisk diagram (Figur 7.2) med relevante slægtskabskoefficienter for beregning af avlsværdiindeks på grundlag af målinger på halvsøskendeafkom (en afkomsundersøgelse).
Herunder er grafisk vis yderligere 3 eksempler på definition af slægtskabskoefficienter for ensartede slægtskabsforhold. Der findes adskillige, flere hvoraf en del vil blive nævnt i nedenstående tabel.
Figur 7.3.
 |
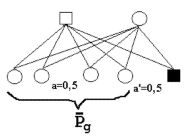 |
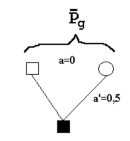 |
Avlsværdiindeks på grundlag af halvsøskendemålinger. |
Avlsværdiindeks på grundlag af helsøskendemålinger. Begge forældre vil have samme slægtskabsforhold til de målte individer, derfor vil et indeks være det samme for en helbroder eller hver af de to forældre. |
Avlsværdiindeks på grundlag af måling af de to forældre. |
I nedenstående tabel er vist opstilling for de estimerede avlsværdier i en række konkrete tilfælde med ensartede slægtskabsforhold. De relevante slægtskabskoefficienter er indsat, og når der er mange (uendelig mange) observationer, er grænseværdierne af regressionskoefficient og den kvadrerede sikkerhed anført.

Tabelparametrene er defineret i afsnit 7.1; den dækker kun et meget
ringe udsnit i brug af formlen, og næsten kun hvor der er pæne løsninger.
Linie 1 i tabel svarer til anvendelse af formel med 0 målinger og man får,
at avlsværdiindekset bliver lig populations gennemsnittet med en sikkerhed på 0,
hvilket giver 'basis' for vurdering af alle de øvrige indeks.
Linie 2 svarer til en meget almindelig situation, den kaldes normalt
individprøve eller phenotypemåling, et dyrs avlsværdi vurderes på grundlag af
måling på dyret selv - ligningen er:
I = A(streg) + h2(P -P-streg) med en kvadret sikkerhed på h2.
Linie 3: der er 2 målinger på dyret selv, det kan f.eks. være kuldstørrelse ved
første og andet kuld. Korrelationen mellem de gentagne præstationer kaldes
gentagelseskoefficienten, den indeholder altid et element af fælles milieu
for de to præstationer.
Linie 4 viser sammenhængen mellem gennemsnits forældre og afkom,
i afsnit 6.4 blev denne relation anvendt til estimering af heritabiliteten.
Linie 7 viser vurdering af en far på grundlag af et uendeligt stort antal afkom,
dette svarer til definitionen af avlsværdi, og man ser at dette er korrekt,
idet vægtfaktoren er lig 2 og sikkerheden lig 1.
Sikkerhed ved avlsværdivurdering
| Figur 7.4. Sikkerhed ved afkomsundersøgelse - afhængighed af antal afkom og heritabilitetens størrelse |
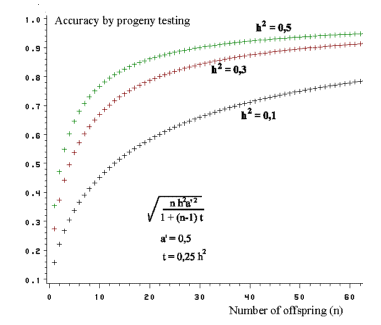 |
Der skal tilføjes et par generelle bemærkninger om sikkerheden på avlsværdibestemmelsen. Ved undersøgelse af formlen for sikkerhed kan udledes:
1) Ved høj heritabilitet er individets egen fænotypemåling
en god informationskilde.
2) Ved lave heritabiliteter kan mange målinger kompensere for ringe sikkerhed ved den enkelte måling. Mange målinger
kan kun skaffes ved store afkomsgrupper, hvor de enkelte dyr enten optræder som afkom eller som hel- eller halvsøskende.
Heritabilitet Størrelse Eksempler ------------------------------------------------------------------- Høj Større end 45 %, Fedtaflejring, fedtprocent i mælk Lav Mindre end 10 %, Reproduktions egenskaber Middel 15-40 %, Tilvækst -------------------------------------------------------------------
En applet til beregning af de mest almindelige tilfælde af avlsværdi findes her, og eksempel på anvendelse ses nedenstående: det fremgår af eksemplet, at 20 stk halvsøskende afkom er en god informations kilde med størst kvadreret sikkerhed.
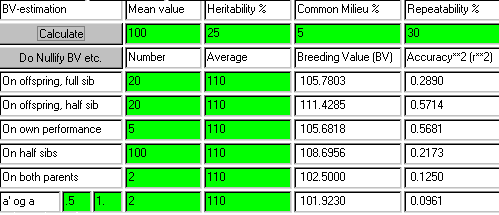
In principles there exist 3 types of information of an animals breeding value, the parents, own performance and offspring. The information from half and full sibs as well as from grandparents are all included in the parent breeding value. This is both a strength and a weakness of the direct updating method as the parents only can be included once. Therefore new information on half and full sibs can not be utilized. Usually it is of little extra value, so in many cases it is an advantage not to bother about this information.
The information to estimate breeding value from the 3 sources has the following forms. The heritability is designated h2 and common environmental variance c2, the estimated breeding value has the symbol A hat. The formulas for combining information from the 3 possible sources can be seen below.

An example on this condition. An index has been made on full sibs offspring and included in the combination index. A new index on more full sib to the first ones cannot be included without violating the rule, as they are related to the old index both through the father and the mother. In contrast half sib offspring can be added when new information comes in, as they are only related through the animal in question.
Do you want to see examples and use an applet for direct updating of breeding values, click here
Avlsværdi estimering er for de store husdyrbrugsorganisationer en sag, der kan give et stort økonomisk udbytte. Der bliver anvendt meget raffinerede metoder, se lektion 12.1. Udover hvad er vist her for estimering af avlsværdi, er det især vigtigt, at der kan ske en korrektion for væsentlige milieu faktorer, som feks. årstid og besætning. Det er endvidere vigtigt, at der samtidig kan tages hensyn til alle beslægtede individers information.
Avlsværdierne kan estimeres på grundlag af store ligningssystemer samtidig for alle dyr. Dette giver mulighed for en simultan estimering af og korrektion for milieueffekter.
Avlsværdiskøn for et dyr kan beregnes på grundlag af alle mulige kombinationer af information. Foreløbigt er der kun vist eksempler, hvor der er anvendt ensartede phenotypemålinger. Der skal her kun vises et par undtagelser fra denne form, hvor den første vedrører bestemmelse af avlsværdi på et afkom på grundlag af forældrenes avlsværdi, her gælder som vist i foregående afsnit at:
Iafkom = (Ifar + Imor)/2 og r2AI,afkom = (r2AI,far + r2AI,mor)/4
Nedenstående er vist ved hjælp af formler hvor meget en genmarkør bidrager i forhold til en phenotypemåling.
Egenskaben har heritabiliteten h2 og genmarkøren alene
repræsenterer en del af den samlede heritabilitet svarende
til (h1)2.
Avlsværdien (I) estimeres således, hvor M står for marker effekt og P for phenotypeværdi:
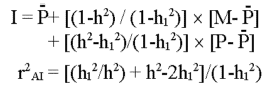
I nedenstående tabel er vist resultater af brug af formlen for sikkerhed uden og med genmarkør (stor effekt, 20 % af den genetiske variation, kolonnerne med +M.
-M +M -M +M -M +M Transferrin locus ------------------------------------------------------------------------------ h2 .05 .05 .25 .25 .50 .50 | .33 (h1)2 0 .01 0 .05 0 .10 | .01 rAI2 .05 .24 .25 .35 .50 .56 | .34
Det fremgår af tabellen, at for egenskaber med lav heritabilitet kan opnås en væsentlig forbedring af sikkerheden ved brug af genmarkør. For egenskaber med høj heritabilitet er forbedringen ringe.
Eksempel: Indeks for en ko med en ydelse på 2300 kg mælk og Tt i transferrintype fra populationen bliver følgende, idet markørgenotypen (M=1882 kg mælk) og middelværdien (Pgns=1904) er taget fra transferrin eksemplet i lektion 6.
Ovenstående formel anvendes og h2 og h12 tages fra tabel
I = Pgns + X*(M - Pgns ) + Y*( P - Pgns ), hvor X = (1-h2)/(1-h12) = (1 - 0,33)/(1 - 0,01) = 0,68 Y = (h2-h12)/(1-h12) = (0,33 - 0,01)/(1 - 0,01) = 0,32 ved indsættelse får man I = 1904 + 0,68*(1882-1904) + 0,32*(2300-1904) = 2016 kg mælk
Sikkerheden, som det ses fra tabellen, forbedres kun svagt ved at medtage transferrintype i indekset.
For estimering af en geneffekt, der påvirker en kvantitativ egenskab, henvises der til lektion 12.
Standardisering af avlsværdi indeks.
De beregnede avlsværdier, udtrykkes normalt i absolutte enheder.
F.eks. kunne man regne sig frem til at avlsværdien for en tyrs daglige tilvækst
fra fødsel til den er 1 år gammel er 1100 gram/dag.
Mange personer har dog vanskeligt ved umiddelbart at vurdere, hvor godt dette resultat er.
Man mangler et sammenligningsgrundlag. Derfor centreres avlsværdierne ofte ved at
trække populationsgennemsnittet fra. Derved har man et relativt mål for avlsværdien i
forhold til populationsgennemsnittet, altså hvor godt det enkelte dyr er i forhold til
alle de andre dyr i populationen. Er populationsgennemsnittet f.eks. 1000 gram tilvækst
pr. dag vil avlsværdien for tilvækst i dette eksempel være 100 gram. Dette svarer til at
individets afkom vil have en avlsværdi på ca. 50 gram/dag i gennemsnit.
Man kan endvidere standardisere avlsværdien ved at dividere med populationsspredningen.
De standardiserede avlsværdier er tilnærmelsesvis normalfordelt med middelværdien nul og
spredningen én.
I Danmark bruges ofte avlsværdi indeks. Indeksene er standardiserede avlsværdiskøn,
der er multipliceret med en ønsket spredning f.eks. 5 og adderet med en ønsket middelværdi
som oftest er 100. Dyr med indeks over 100 er bedre end gennemsnittet
og dyr med indeks lavere end 100 er dårligere end gennemsnittet.
1. Selektions differens og -intensitet
3. Selektion på tærskelegenskaber
4. Genetisk korrelation, ændring i sekundære egenskaber
- Lyd og billed show (real player should be installed) eller Billed show
5. Opgaver
| Figur 8.1. Viser en grafisk fortolkning af selektionsdifferens (S) og den standardiserede selektionsdifferens (i), samt selektions response (delta G) ved individuel selektion. |

|
I ovenstående figur er endvidere vist forbindelsen mellem bestemmelse af avlsværdi og den simple formel for selektions resultat R = h2 * S fra lektion 6, til den generelle formel for delta G, der vises på næste side.
Nedenstående er vist en tabel over 'i' som afhængig af proportion af dyr udvalgt til avl.
Proportion Intensitet Proportion Intensitet Proportion Intensitet af dyr til i af dyr til i af dyr til i avl avl avl ------------------------ ----------------------- ---------------------- 1,00 0 0.90 0,20 0.09 1,80 0.008 2,74 0.80 0,35 0.08 1,85 0.006 2,83 0.70 0,50 0.07 1,91 0.004 2,96 0.60 0,64 0.06 1,98 0.002 3,17 0.50 0,80 0.05 2,06 0.001 3,38 0.40 0,97 0.04 2,15 0.0008 3,43 0.30 1,14 0.03 2,27 0.0006 3,51 0.20 1,40 0.02 2,42 0.0004 3,61 0.10 1,76 0.01 2,67 0.0002 3,79
Eksempel på tabelopslag: Skal der anvendes 30% af dyrene til avl bliver i = 1,14.
I nedenstående figur er vist den generelle formel for forventet ændring ved selektion. Ændringen er proportional med
selektionsintensiteten, sikkerheden ved avlsværdiestimeringen og den additive spredning. Ændringen per tidsenhed er
omvendt proportional med generationsintervallets længde.
Generationsintervallets længde er defineret som forældrenes gennemsnitlige alder, når afkommet fødes. Eksempel: I den
humane population siger man, at generationsintervallet er 30 år,
dvs. at et gennemsnits forældrepar er 30 år, når deres barn bliver født.
Generel formel for selektionsrespons 'fremgang', ændring benævnes som delta
G

I langt de fleste tilfælde er der forskellige reproduktionsmæssige forhold for de to køn, så alle parametre i ovenstående formel er forskellige for de to køn. Derfor er det nødvendigt at opdele bidraget til den nye generation i to, hvorfra den ene kommer fra mødrene, og den anden kommer fra fædrene. Hvert af de to køn bidrager med halvdelen af arveanlæggene til næste generation.
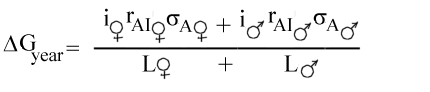
En applet til beregning af selektions respons kan anvendes klik her
Formlerne for delta G har stor værdi til at forudsige, hvad man kan forvente sig fra et givet avls program, men deres vigtigste funktion er anvendelse til modelstudier, hvor man kan designe et optimum med hensyn til balance mellem generationsinterval, intensitet og sikkerhed. Ved korte generationsintervaller bliver der født færre individer at selektere iblandt. Dette påvirker både intensiteten og sikkerheden i negativ retning.
Fra lektion 1 kan repeteres, at en tærskelegenskab nedarves som en kvantitativ egenskab. Der er blot det særlige, at egenskaben kommer til udtryk som en enten/eller egenskab, f.eks sygdommen mastitis hos malkekvæg, eller hjertefejl hos en nyfødt hundehvalp.
Antal mastitisudbrud hos en ko kan derimod betragtes som en semikvantitativ egenskab, især når det gælder et helt livsforløb med mange laktationer. For antal tilfælde af mastitis vil der ikke være tvivl om, at der er en rimelig lineær sammenhæng mellem antal tilfælde og dyrets resistens mod sygdommen.
Der kan i andre tilfælde være betydelig mere tvivl om, at man har at gøre med en lineær skala. Der kan her henvises til den såkaldte 'pind og fjertest' hos mink for at teste dyrenes reaktionsmønstre. Man har klasserne for mulige udfald aggressiv, nysgerrig og frygtsom, der måles i samme test. Men vil det overhovedet være relevant at sætte de tre klasser på en lineær skala og i så fald hvordan?
For at få en mening i en sådan test må man arbejde med tre uafhængige tærskelegenskaber der bliver 1) aggressiv eller ikke aggressiv 2) frygtsom eller ikke frygtsom og 3) nysgerrig eller ikke nysgerrig, se figur 8.2.
| Figur 8.2.
De tre karakteristika aggressiv, frygtsom eller nysgerrig kan ikke fortolkes som lineære med fælles skala, men må fortolkes hver for sig med hver sin skala. |
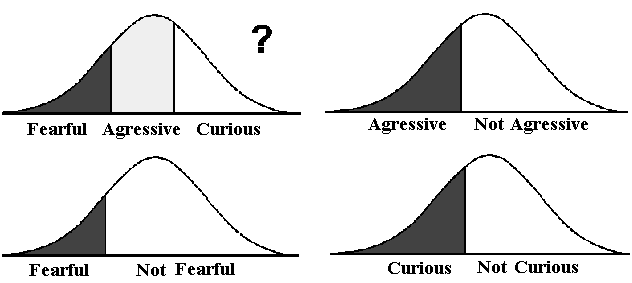 |
Eksempel: Hofteledsdysplasi (HD) hos Schæferhunde gengivet fra Andresen et al. HD indeks: Bedømmelsen bør bruges efter hensigten. Hunden dec.1994.
Som det ses af figuren er skalaen ikke lineær, målt på en normalfordelingskurve. Ved beregning af HD indeks bruges klassemiddel i stedet for en lineær ti delt skala. Klassemiddel er fastsat ud fra en normalfordeling med middelværdi 0 og en standardafvigelse på 1.
| Figur 8.3.
Delvis lineær skala af graduering af HD. Antallet i hver klasse er tilpasset normalfordeling-en. |
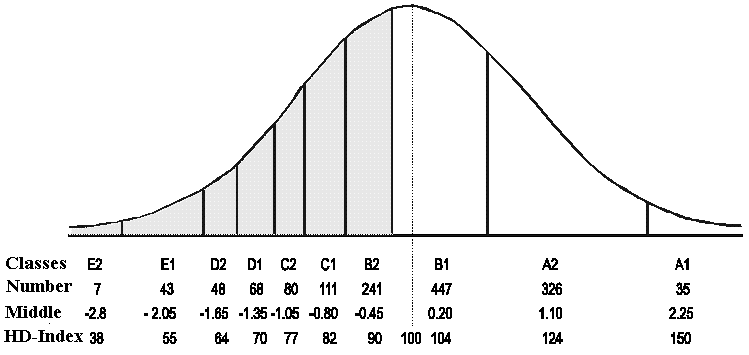 |
Estimering af avlsværdi for en hanhund på grundlag af 15 stk afkom er vist nedenstående. Afkommet var fordelt med 4 A2, 9 B1, 1 B2 og 1 D1. Avlsværdien ganges med 100 og der adderes 100 til avlsværdien, så dyr der har et indeks på over 100 er bedre end gennemsnittet. Der henvises i øvrigt til formler i lektion 7

Det beregnede indeks er betydeligt over gennemsnittet, hvilket også fremgår af at hannen kun har to stk afkom med B2 og nedefter.
Det beregnede avlsværdi-indeks kan standardiseres således, at det feks varierer mellem 50 og 150. Nærværende indeks på 127, er vilkårligt 'standardiseret' med faktoren 100.
I figur 8.4 er vist røntgenbillede af de bedste hofter A1 og de værste E2. Billederne er taget på Røntgen-Klinikken her ved KVL.
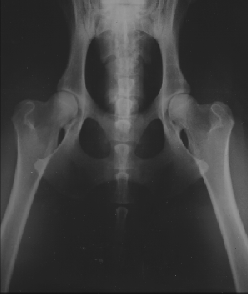 ..
..
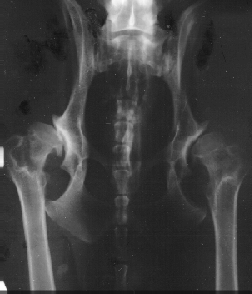
Applet til beregning af avlsværdier i flere generationer, klik her
Fra april år 2000 er DKK gået over til en fem trins skala
ved HD bedømmelsen, hvilket svarer til den anerkendte internationale
HD skala, så nu findes der kun A, B, C, D og E klasserne. I nærværende eksempel er
de nye klasse værdier 1,21, -0,02, -0,90, -1,47 og -2,16, hvorpå der kan regnes HD-indeks.
Sammenligning af familievis forekomst af tærskelegenskaber og
Mendelske egenskaber. I lektion 5 er der redegjort for
nedarvningsforholdene for Mendelske egenskaber. Alle disse former optræder familievis,
og det samme er tilfældet for
tærskelsygdomme.
For sygdomme med lav populationsfrekvens vil man ikke kunne skelne mellem Mendelske nedarvede sygdomme og en
tærskelsygdom. I begge tilfælde vil frekvensen af sygdommen være meget højere hos nære slægtninge til en syg end
frekvensen i populationen.
Differentieringen mellem de to former for nedarvning kan kun ske på grundlag af testparringer, hvor man i tilfælde af
Mendelsk nedarvede sygdomme kan forudsige det nøjagtige udspaltningsforhold, hvilket ikke er tilfældet for tærskelsygdomme.
| Figur 8.5.
Beregning af heritabilitet på grundlag af sygdomsfrekvens hos slægtninge til syge dyr. |
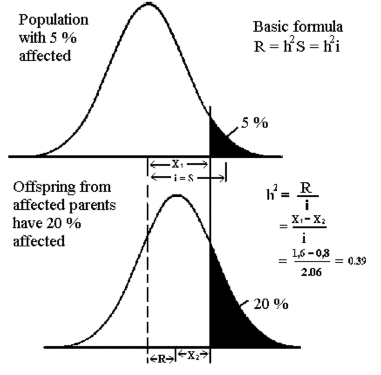 |
Heritabilitets estimering for tærskelegenskaber.
I lektion 6 er der redegjort for
heritabilitetsestimering for normalt fordelte egenskaber.
Heritabilitet kan estimeres for en tærskelsygdom når man kender populationsfrekvensen
og frekvensen hos afkom efter syge dyr eller slægtninge til syge dyr.
I eksempel, figur 8.5, er vist ideen i beregningen i grafisk form.
Frekvensen i populationen er 5 % og frekvensen hos afkom, hvor begge forældre er syge, er 20 %.
Situationen kan opfattes som et selektionseksperiment, hvor der kun avles videre med syge dyr.
Vi bruger nu den almindelige formel for beregning af heritabilitet R = h2S
på data fra et selektionsforsøg,
hvor vi i arbejder direkte på den standardiserede normalfordeling med S = i. Responset
R findes som differencen mellem
X1 og X2, der kan slås op i en tabel over normalfordelingen.
Selektionsintensiteten (i) findes ligeledes ved tabelopslag.
Heritabiliteten bestemmes til 0,39.
Kendes frekvensen af syge dyr hos f.eks. første grads slægtninge, far, mor eller
helsøskende gennemføres beregningerne
som i viste eksempel, men så er det h2/2 der estimeres ved forholdet R/i, anvendes data fra
anden grads slægtninge som f.eks halvsøskende estimeres h2/4.
En opgørelse af nærværende type kan også betragtes som en epidemiologisk undersøgelse hvor risikofaktoren er at være beslægtet med et sygt individ. Den relative risiko for at blive syg er 20%/5% = 4 gange så stor hos afkom, hvor begge forældre er syge, som hos et tilfældigt individ i populationen.
Applet til beregning af heritabilitet og relativ risk for tærskel egenskaber
Effekten af gener i et locus kan påvirke flere egenskaber. Dette medfører, at når der ved selektion sker ændring af en egenskab, vil der, såfremt der er flersidig virkning af de underliggende gener, ske ændring i andre sekundære egenskaber.
Der vil ofte forekomme overraskende resultater. Derfor er det vigtigt, at et selektionsprogram bliver overvåget nøje for at undgå uheldige sekundære ændringer. Er der sammenhæng mellem ændringer i to egenskaber, siger man at de er genetisk korrelerede. Genetisk korrelation kan være positiv eller negativ med talstørrelser fra -1 til +1. Genetisk korrelation har symbolet rA1,A2, hvor A1 og A2 er avlsværdier af de to egenskaber 1 og 2.
Et eksempel fra kødkvægavl. Der selekteres for store kalve ved fødsel - såfremt køernes udvoksede vægt ikke ændres samtidig, vil det uvægerligt resultere i kælvningsbesvær, idet forholdet mellem kalv og koen, der skal føde, ændres i ugunstig retning.
| Figur 8.6.
Viser todimensional fordeling med en negativ korrelation på -0,5. Den skrå linie viser selektionsgrænse ved udvalg efter indeks selektion |
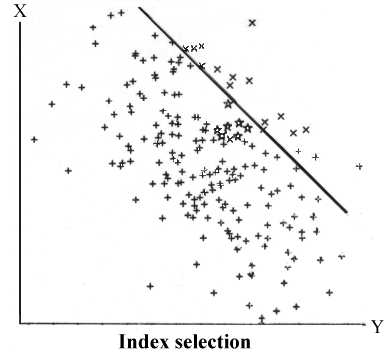 |
I figur 8.6 er vist en todimensional fordeling med negativ genetisk korrelation på 0,50 mellem egenskaberne X og Y. Selektionsgrænse (den skrå linie) er lagt, så der er lagt lige meget vægt på de to egenskaber. Som det ses, er det svært at forbedre begge egenskaber ret meget når der er negativ genetisk korrelation. Omvendt går det meget lettere, såfremt egenskaberne har positiv genetisk korrelation i forhold til den ønskede selektionsretning.
Der tales om tre forskellige udvalgskriterier
Tandem selektion foregår med en selektion af egenskab ad gangen
Uafhængig selektion, her sættes selektionsgrænserne
uafhængigt for hver egenskab
Indeks selektion, her vægtes egenskaberne i forhold til deres økonomiske betydning
Det er svært at bestemme den genetiske korrelation, idet den kan variere meget fra population til population, og den varierer meget mere over tid end heritabiliteten. Der skal dog gives en formel til beregning af realiseret genetisk korrelation. Når der selekteres for egenskaben x og der samtidig sker ændring i egenskaben y, kan den genetiske korrelation bestemmes som:
rAx,Ay = (delta Gy/sigmaAy)/(delta Gx/sigmaAx)
Den genetiske korrelation bestemmes altså som forholdet mellem de standardiserede selektions resultater, når der kun selekteres for egenskaben x, og egenskaben y følger passivt med.
Der er en tendens til at der ved selektion gennem mange generationer vil opstå en uheldig genetisk korrelation mellem den egenskab, man selekterer på og 'fitness'. Dette giver sig udslag i, at der hele tiden skal være et selektionstryk på egenskaben for at holde den på det niveau, hvortil man er nået. Opgives selektionen, vil populationen gå tilbage mod udgangspunktet hvor der er optimal fitness.
| Figur 8.7.
Viser at ved store ændringer af en egenskab er det ofte også nødvendig at ændre miljøforholdene for at opnå maksimal effekt (læses harmoniske dyr) ved udnyttelse af interaktionen. |
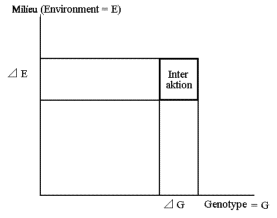 |
Ved store ændringer både i milieu-forhold eller genetisk baggrund, bliver interaktionen mellem genetik og milieu en nødvendig faktor at forholde sig til. Interaktionen afspejler den negative korrelation til fitness.
Selektionsforsøg til belysning af genetisk korrelation. I figur 8.8 er vist tre parallelle selektionsforsøg med
slagtekyllinger gennemført af Australieren Pym, der har offentliggjort resultaterne i 1982. Forsøget gik over 10 generationer, og måleperioden var fra 5 til 9 ugers alderen. der er selekteret for henholdsvis Weight gain (W), Food consumption
(F) og Food conversion rate (E) i de tre forsøg, og kurverne for de tre egenskaber har betegnelserne W, F og E.
Samtidig med at man har målt det direkte selektionsrespons, har man også målt, hvordan det er gået med de to andre
egenskaber. At de ikke-selekterede egenskaber også ændrer sig er udtryk for genetisk korrelation. Det kan endvidere ses, at
selektionen resulterer i vidt forskellige kyllingetyper afhængigt af, hvilken egenskab der selekteres for.
| Figur 8.8.
Selektionsforsøg med slagtekyllinger til belysning af genetisk korrelation gennemført af Australieren Pym. Forsøget gik over 10 generationer, og måleperioden var fra 5 til 9 ugers alderen. der er selekteret for henholdsvis Weight gain (W, øverste graf)), Food consumption (F, mellemste graf) og Food conversion rate (E, nederste graf). De korrelerede resultater er vist i de andre grafer, så F i øverste graf refererer til korreleret respons for W ved selektion for F, o.s.v.. |
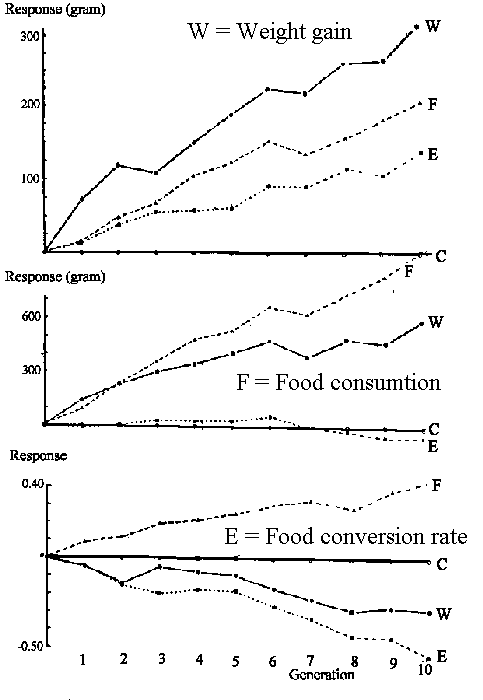 |
Dyr der selekteres for tilvækst (øverste graf W) får også et større fødeindtag
(mellemste graf W) og en bedre effektivitet (nederste graf W) lavere foderforbrug
per kg tilvækst.
Dyr der selekteres for foderforbrug (mellemste graf F) får også en større tilvækst
(øverste graf F) og en dårligere effektivitet (nederste graf F) højere foderforbrug
per kg tilvækst.
Dyr der selekteres for effektivitet (nederste graf E) får også en større tilvækst
(øverste graf E) og et uændret foder indtag (mellemste graf E).
Video klip af stærkt selekterede kyllinger for dgl. tilvækst
med korrelerede benproblemer,
(kræver installation af Real Audio)
Video klippene stammer fra en udsendelse fra DR 'Journalen' og er optaget på
Danmarks Jordbrugsforskning, Foulum, hvor prof. Poul Sørensen har stået for
den faglige information.
Video klip
af kyllinger, der er selekteret for stor dgl. tilvækst, og en tilsvarende æglægger. Ved
5 uger vejer den hvide slagtekylling ca. 2 kg, der er ca 4 gange vægten af den brune
æglægger kylling.
Video klip
af kyllinger der er selekteret for stor dgl. tilvækst, der som korreleret effekt får
benproblemer. Den først viste kylling har så svære benproblemer, at den ikke kan
klare at få føde og vand, den bør aflives. Kylling nummer to går dårlig, og den
har gang som en sømand der ved at skræve får balance i kroppen.
Auto selektion for egenskaben kuldstørrelse - balance med fitness.
| Figur 8.9.
Viser kuldstørrelse som egenskab for søerne og som egenskab hos de fødte grise, der er som vist 1 gris til forskel mellem de to middelværdier, der svare til en selektionsdifferens på 1 i hver generation. |
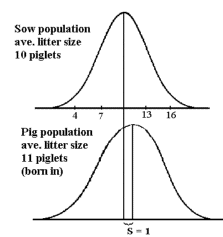 |
Der er i hver generation en auto selektion for højere kuldstørrelse, da der bliver født flest grise i de store kuld. Det kan vises, at der er en selektions- differens på en gris for højere kuldstørrelse i hver generation, se figur 8.9. Egenskaben kuldstørrelse er normal fordelt når man ser på egenskaben fra søernes side, men egenskaben født i kuldstørrelse er højreskæv, da der som før nævnt bliver født flest grise i de store kuld. Denne selektion må nødvendigvis balanceres af at de grise der er født i store kuld har lavere fitness end dem der er født i små kuld.
Den maternelle påvirkning for en grises videre skæbne er positiv for grise født i små kuld og negativ for grise født i store kuld. Ved udtagning af sopolte bør man derfor undgår individer født i store kuld. Den negative maternelle effekt gør sig især gældende i dyrearter, hvor kønsmodenhed indtræder før dyrene er udvoksede.
Tilbageslag efter ophørt selektion for egenskaber hvori fitness indgår.
Såfremt man ved selektion har ændret en egenskab meget vil den ofte gå tilbage mod
udgangspunktet når selektionen ophører. F.eks. tamsvin har en kuldstørrelse omkring 10,
hvorimod deres stamfædre, vildsvinet, kun har en kuldstørrelse på det halve. Man kan
derfor forvente, at såfremt man lader tamsvinet gå tilbage til naturtilstanden vil
kuldstørrelsen efterhånden tilpasse sig til de forhåndenværende ressourcer. De samme
synspunkter vil også være gældende for højtydende malkekøer såvel som for æglæggere eller
slagtefjerkræ.
De højt specialiserede husdyrracer vil kun kunne opretholde den store produktion,
i det omfang der bliver sørget for dem hvad angår indhusning og fodertildeling.
1. Effekt af indavl på individuelt og populationsniveau
5. Populations struktur, avlspyramide
- Lyd og billed show (real player should be installed) eller Billed show
6. Opgaver
Forventningen til præstationen er mindre når man taler om indavlede dyr.
Ved indavlsdepression forstås et fald i produktion eller livskraft, der er
proportional med indavlsgraden. Krydses to racer eller linier ophæves al
akkumuleret indavl. Den største krydsningsfrodighed (heterosis) opnås ved en tre
vejs krydsning. Minimum indavl kan sikres, når alle forældre får lige meget afkom.
Fuldstændig indavl kan hos laboratoriedyr opnås efter 20 generationers helsøskende
parring. De fleste forsøgsdyr indenfor mus og rotter er 100% indavlede, genetisk
set er de da helt homozygote og identiske.
------
I afsnittet om individuel indavl blev vist, at indavl forøger chancen for homozygoti for et enkelt lokus. Det samme gælder for homozygoti generelt. Ved indavl øges homozygotien, mens antallet af heterozygoter falder. Ved 100 procents indavl er der ingen heterozygoti tilbage.
Hvad der gælder for et enkelt individ, gælder også for populationer. Går vi tilbage til albumin eksemplet fra hunde, som vist i lektion 2.4 findes, at der mangler 16 procentenheder af heterozygoterne; opdeling i subpopulationer (racer) hos hunde giver anledning til indavl indenfor de enkelte racer, der kan beregnes til 33%.
Det er kendt, at der sker et vist fald i livskraft og produktion som følge af indavl og det kan vises, at der er en lineær sammenhæng mellem produktionsegenskaber og indavlsgraden. Derfor er det nødvendigt at sikre en så lav indavl hos produktionsdyr som vel muligt. Dette gøres ved at sammenligne stamtavler før parring, eller ved mere robuste systemer. Som f.eks at man holder dyrene opdelt i flokke hvor, hunnerne forbliver i flokken, mens de nye hanner flyttes til en anden flok. Et sådant system kan sikrer gennemsnitlig lav indavl, se skitse i afsnit 9.3 for helsøskendeparring under minimum indavl.
Faldet i produktionsegenskabernes niveau kaldes indavlsdepression og er af størrelsesorden 0,4 enheder for en enheds stigning i indavlsgrad. For reproduktionsegenskaberne derimod er faldet 1 enhed for en enheds indavlsstigning. Det sidste bevirker, at det er meget svært at producere 100 procents indavlede husdyr.
I figur 9.1 er vist det lineære fald i dgl. slagtetilvækst hos svin. Liniens hældning er 2.1 grams fald for en enheds stigning i indavlsgraden (data fra Christensen et al. Anim Prod. 58:298-300, 1994).
| Figur 9.1.
Fald i dgl. tilvækst i relation til indavl hos grise |
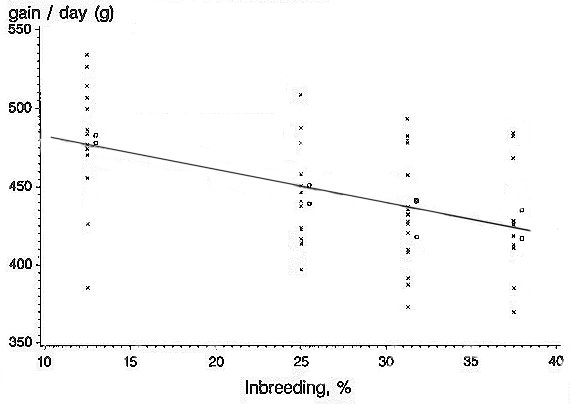 |
Det lineære fald i produktionsevne kan henføres til et lineært fald i heterozygotigraden, der er proportional med stigningen i indavlsgrad. Der sker tilsvarende en øgning i homozygotigraden, der er lige stor for begge de homozygote typer. For det enkelte locus er faldet proportional med 2Fpq, og de tilsvarende stigninger er Fpq, se tabel i afsnit 4.4. Indavlsdepressionens størrelse er tillige afhængigt af dominansafvigelsernes størrelse, der er konstante for en given egenskab. Indavlsdepressionen er generelt størst for egenskaber med lav heritabilitet.
Effekt af krydsning er den omvendte set i forhold til indavl. Krydsningsdyr er mere heterozygotiske end individer i en udavlet population. Men når det drejer sig om at forudsige effekten af krydsning, findes der ikke umiddelbart metoder til at bestemme denne, som det var tilfældet med indavl, hvor der er en lineær negativ sammenhæng mellem fitness samt produktionsegenskaber og indavlsgraden.
Hvordan kan der så etableres fornuftige krydsningssystemer? Man må desværre sige, at den eneste metode er 'prøv og fejl' metoden. Store dele af den praktiske fjerkræ-, mink- og svineproduktion foregår på grundlag af krydsninger, så 'prøv og fejl' princippet er måske ikke så dårligt endda. Er der først fundet en kombination, der udviser krydsningsfrodighed eller heterosis, kan denne kombination gentages i det uendelige, da en given krydsningsfrodighed tilsyneladende er uafhængig af, at man tillige forbedrer renavls dyrene. Renavl er ikke defineret tidligere, men ordet hentyder til, at der hverken sker indavl eller krydsning, så avl i en større population af husdyr betegnes som renavl.
| Figur 9.2. Krydsningssystemer |
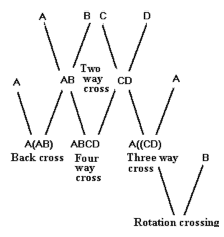 |
Krydsningsfrodighed er som ordet siger en speciel frodighed, der opstår som følge af krydsning. Den arter sig ved, at man får mere robuste dyr med større produktionsevne end renracedyrene. Heterosis er udtryk for det samme som krydsningsfrodighed. Ordet stammer fra engelsk og antyder, at effekten skyldes forøget heterozygoti.
Krydsningsystemer. I figur 9.2 er der vist fire racer eller linier A, B, C og D. Krydsning kan gennemføres som tovejs, trevejs eller firvejskrydsning, tilbagekrydsning, eller rotationskrydsning.
i figur 9.3 er vist et eksempel på krydsningsfrodighed fra mus målt som det antal unger en hunmus kan få på livstidsbasis. Der er her anvendt et af de mest populære krydsningssystemer: to- og tre- vejs-krydsning, og tilbagekrydsninger (data fra Newman et al. J.Anim. Sci. 61 358-365, 1985).
| Figur 9.3. Effekt af krydsning på frugtbarhed hos mus |
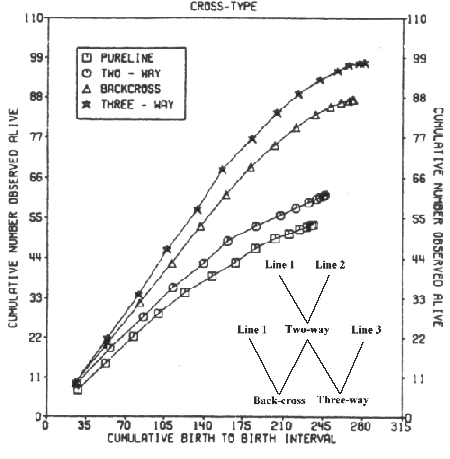 |
Effekterne kan opdeles i en effekt på fosteret og en effekt på moderegenskaber. Effekten, om fosteret er en krydsning eller ej, aflæses af forskellen mellem de to nederste kurver, hvor den nederste repræsenterer et renavlsfoster i en renavlsmor. Den næstnederste kurve repræsenterer et krydsninngsfoster i en renavlsmor. Effekten af, om hunmusen er en krydsning eller ej, aflæses af forskellen mellem de nederste to kurver og de to øverste. Det ses, at den største del af krydsningsfrodigheden ligger på den maternelle del. Her drejer det sig om evnen til at ovulere mange æg og evnen til at bringe dem frem til fødsel.
Så store krydsningsfrodigheder som er vist i ovenstående eksempel er sjældne, men set i
forbindelse med husdyrproduktion, er det ikke usædvanligt at se effekter på op til 10
procent.
Krydsningsfrodighed beregnes som (krydsningernes gennemsnitlige værdi minus gennemsnit
af de rene racers gennemsnit) i forhold til de rene racers gennemsnit.
Eksempel: Landrace Yorkshire krydsningssøer giver en ekstra gris per kuld
i forhold til renrace søerne, der har en gennemsnitlig kuldstørrelse på ca. 10.
Krydsningsfrodighed = (11 - 10)/10 = 0,10 eller 10% for kuldstørrelse hos svin af nævnte kombination.
For at et produktionskrydsningsprogram skal kunne gennemføres, er det nødvendigt at der bagved foreligger avl med de rene racer eller linier. Krydsning kræver, at der er et overskud af avlsdyr. Dette er feks. ikke tilfældet inden for de danske malkekvægracer. Her skal man stort set bruge alle de fødte hundyr til avl, idet hver ko af RDM og SDM i gennemsnit kun føder 1,1 til 1,2 kviekalve, hvilket lige er tilstrækkeligt til at opretholde bestanden. Rotationskrydsning vil dog kunne praktiseres udenfor den egentlige renavlskerne, men her er krydsningsfrodigheden betydelig lavere end ved trevejskrydsning.
En ekstra fordel ved krydsning består i at dyrene bliver mere ensartede, når der er mindst en renavlet forældre race. I en tysk undersøgelse over spæk tykkelsen hos svin er der fundet, at den phenotypiske varians er reduceret med ca. 30 procent hos L x Y krydsninger i forhold til renrace dyr (Lutaaya et al. 2001, 79:3002-07).
| Figur 9.4. To genpar og biokemi: Nye kombinationer, AAbb og aaBB, er ikke altid heldige ved udspaltning i F2 |
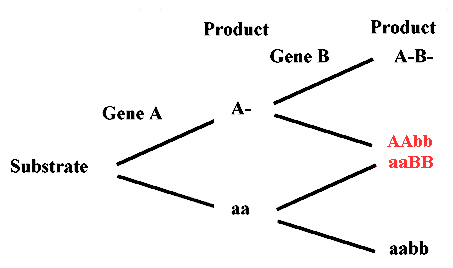 |
Indkrydsning: Vil man forbedre en race ved indkrydsning, vil man normalt anvende
tæt beslægtede racer med de ønskede egenskaber. Man ønsker normalt også at det
bedste af den oprindelige race bevares. Skal dette ske må der ikke selekteres for stærkt
i de første generationer af indkrydsningen, da det ved indkrydsning er de
rekombinante typer, der er af interesse, og det tager tid før de forekommer.
| Figur 9.5. Kromosomer fra oprindelig og indkrydset individ før rekombination. |
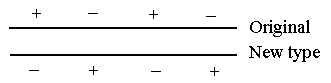 |
I mindre populationer vil man gerne holde den generelle indavlsstigning på et så lavt niveau som muligt. En af måderne, man kan reducere indavlen på, er at sørge for, at alle dyr får lige meget afkom der fortsætter som avlsindivider. I princippet skal hvert individ være far eller mor til et hanligt og et hunligt afkom. Er dette tilfældet, vil den effektive populationsstørrelse være 2 gange den faktiske. Dette skyldes, at man ved tilfældig sammenparring i en H-W population i princippet vil have en fordeling af afkom pr individ, der svarer til en venstreskæv binominalfordeling (en Poissonfordeling) med middelværdi to, og derved vil fordeling af afkom pr individ være 0, 1, 2, 3, 4 som de hyppigste. Dvs. der er en del individer, der slet ikke får afkom.
For at sikre minimal indavl er det nødvendigt at arbejde systematisk, og de bedste systemer går på cirkulær parring.
I figur 9.6 er vist cirkulære halvsøskende- og helsøskendesystemer, hvor
helsøskendesystemerne er dem der lettest finder praktisk anvendelse. Halvsøskende systemet
gentages på samme måde i hver generation, hvorimod helsøskende systemet har en cyklus på
to generationer.
Den praktiske udformning er næsten kun mulig for helsøskende, idet der ved halvsøskende
er nødvendigt at hunnen føder 2 gange, for at dens afkom kan være halvsøskende. Helsøskende
systemet gennemføres hos mus ved at lade hun ungen blive i den kasse, hvor den er født, hvorimod
dens helbroder flyttes til kassen ved siden af.
| Figur 9.6 Cirkulære parrings systemer med minimum indavl. |
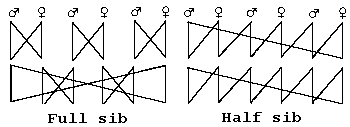 |
Indenfor laboratoriedyr som f.eks. mus, rotter, marsvin og kaniner har det været muligt at opnå fuldstændig indavlede dyr. Teoretisk vil man ved fortsat helsøskendeparring opnå 99,8 procents indavl efter 20 generationers forløb. Ved fortsat helsøskende parring eller forældre-afkom parringer er indavlsgraden bestemt af indavlen i de to foregående generationer, og man har Fn = (1 + 2*F(n-1) + F(n-2))/4, hvor Fn er indavlen i generation n, se løsning til opgave 4.2. De totalt indavlede stammer har den fordel at de genetisk set er fuldstændig ens, så i forbindelse med afprøvning af f.eks. nye lægemidler kan man nøjes med et mindre antal forsøgsdyr end ved anvendelse af udavlede dyr, da fejlvariansen er mindre. For at opretholde ensartetheden er det nødvendigt, at man hele tiden anvender helsøskendeparringer, og når der skal anvendes mange dyr til et forsøg, skal opformeringen ske på en sådan måde, at der maksimal er 5 generationer tilbage til det par hvorfra de alle stammer. Årsagen til at man skal være så omhyggelig ligger i det forhold, at ethvert nyt individ bærer et vist antal nymutationer, disse mutationer bliver meget synlige på en indavlet baggrund.
Det har ikke været muligt at nå fuldstændig indavl indenfor vore almindelige husdyr arter. Når indavlen er nået op til en 60-70 procent har fertiliteten på grund af indavlsdepressionen været så meget reduceret, at det ikke har været muligt at nå videre. For laboratoriedyrenes vedkommende er man nået igennem den barriere, og det har vist sig, at de stammer der først er blevet 100 indavlede kan have en høj og stabil fertilitet.
Hver indavlslinie, der bliver opretholdt kommerciel, er specialiseret til helt specifikke formål, som f.eks. diabetes mus, der let får diabetes. De anvendes naturligvis indenfor diabetes forskningen. Der findes også en lang række transgene stammer af både rotter og mus, hver specialiseret til sit formål. Link til udbydere af laboratoriedyr.
Indenfor produktionsdyr som f.eks. svin og høns sker produktionen stort set kun på grundlag af krydsningsdyr. For at der kan opretholdes en fortsat produktion af krydsningsdyr er det nødvendig at der drives renavl med hver af racerne, der indgår i krydsningssystemet.
I et sådant system vil man tale om en avlspyamide med tre følgende tre led:
| Figur 9.7. Avlspyramide med renavl i
avlsbesætninger i dansk svineproduktion |
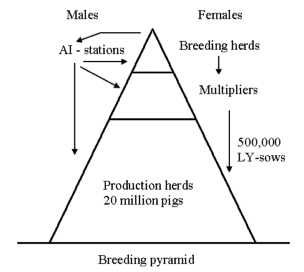 |
1. Fremstilling af kromosom præperater
2. Normale karyotyper fra husdyr
4. Identifikation af kromosomer med kromosom paint
5. Kromosomfejl påvist ved DNA-indhold i sædceller
- Lyd og billed show (real player should be installed) eller Billed show
Der beskrives simple metoder til fremstilling af kromosompræparater,
og normal karyotypen beskrives for alle vore husdyr. Karyotypen går fra minkens
30 til hundens 78 kromosomer. Minken har flest meta- og submetacentriske og hunden
næsten kun acrocentriske kromosomer. Der gives en opsummering af de mest almindelige
kromosomfejl hos husdyr, og metoder til at påvise dem. Der bliver omtalt
flow-cytometri af sæd, hvor sædcellerne kan opdeles i to populationer - en der
har Y-kromosomet og en der har X-kromosomet. Spermatozoer fra translokationsdyr
vil udvise flere end de to populationer.
-----
Det er kun under cellens metafase, at kromosomerne bliver synlige og egnede for den klassiske kromosomanalyse. Da metafasen er meget kortvarig, er det nødvendigt at have celler i stærk vækst for at kunne fremstille kromosompræparater.
Dyrkning af lymfocytter er den mest anvendte metode til at få mange celler i metafase. Lymfocytterne er normalt inaktive celler, og cellerne skal derfor stimuleres for at dele sig. Det mest almindelige anvendte mitogen (mitosestimulator) er PHA (phytohaemagglutinin), der er en ekstrakt fra bønner.
Følgende procedure anvendes for 'blod' kultur:
Kromosomer kan også fremstilles fra fibroblast celle kulturer, der feks. kan etableres fra et øreklip eller subcutan muskelvæv. Kulturen skal etableres inden for det første døgn efter prøvens udtagning. Cellekulturen skal vokse omkring 2 uger før der er tilstrækkelig mange celler til fremstilling af kromosompræperater. Dyrkningsmedierne kromosom præperationsmetoderne er de samme som nævnt under 'blod' kultur, men der skal dog ikke anvendes PHA.
For at identificere de enkelte kromosomer anvendes båndfarvning. Dette gøres ved at dyrke cellerne de sidste 6-7 timer (afhængig af væksthastighed) før høst med tilsætning af en tymidin analog Brom-deoxy-Urasil (BrdU). Ved farvning med Acridin orange vil BrdU inkorporation give matte bånd i de områder, der replikerer sent (efter tilsætningen af BrdU), hvorimod de tidligt replikerende områder giver en kraftig farve. Ved hjælp af denne farvning kan demonstreres inaktivering af et af hunnens X-kromosomer, idet det inaktiverede X-kromosom har ekstrem sen replikation, se lektion 2.2
Metafasekromosomer bliver ved lufttørringsmetoden spredt på tilfældig måde i et plan på objektglasset. Ved fotografering udvælges celler hvor kromosomerne ikke overlapper, og hvor kromosomerne samtidig er så lidt kontraherede som muligt, se feks. blåræve metafasekromosomerne, der er vist i afsnit 10.3.
Når kromosomerne er båndfarvede, kan de sættes op
parvis, som vist i figur 10.1. De er sat op ifølge internationalt
anerkendte nummereringsmetoder. Nummereringsmetoderne går i store
træk ud på at ordne dem efter størrelse og/eller centromerets
placering. Indenfor hvert kromosompar stammer det ene fra dyrets far og
det andet fra dyrets mor. Hver husdyrart har specifikke kromosomer både med hensyn
til antal og form, antallet går fra minkens 30 til hundens 78. Dyr med mange
acrocentriske kromosomer har normalt flest, så hos hunden er der næsten kun
acrocentriske, hvorimod mink næsten kun har metacentriske kromosomer.
| Figur 10.1.
Kvæg kromosomer, 2n=60,XY, farvemetode BrdU inkorporation - Acridin Orange 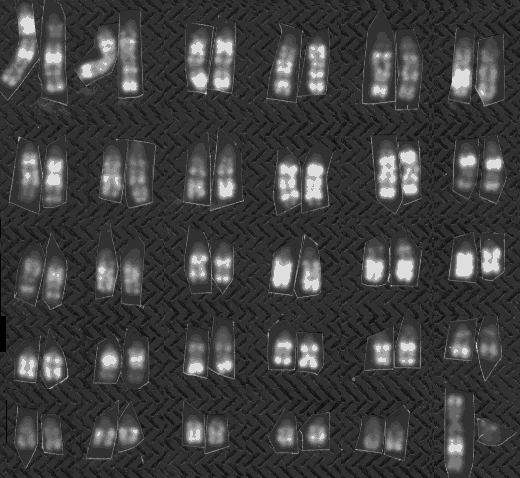
Svinekromosomer, 2n=38,XX 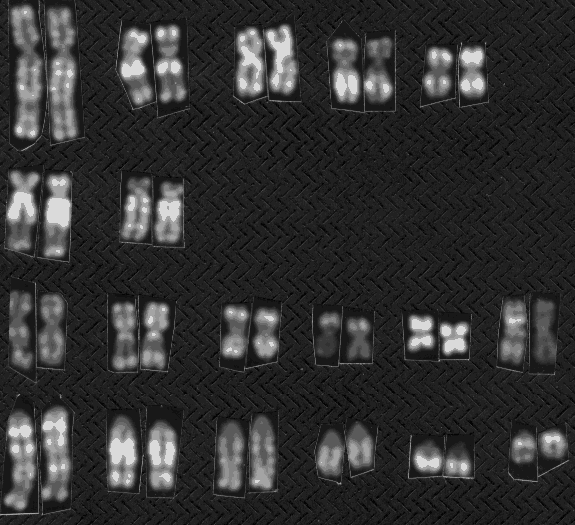 |
. . Kattekromosomer, 2n=38,XX
. . 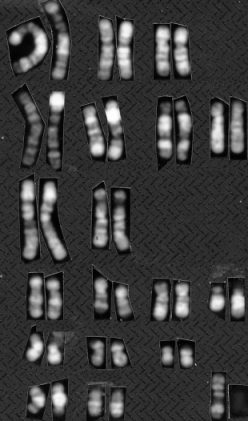 |
Der er stor lighed mellem kvægets kromosomer og kromosomerne fra får og ged. Geden
har 60 kromosomer, der stort set er identisk med kvægets lige bortset fra
kønskromosomerne X og Y. X-kromosomet hos ged er acrocentrisk og
Y-kromosomet er meget mindre end kvægets. Hos får er der de samme forskelle med
hensyn til kønskromosomerne, men herudover er der sket 3 centromerfusioner for
kromosomerne
1/3, 2/8 og 5/11 i forhold til kvæg og ged, derfor har får 54 kromosomer.
Der kan forekomme normale fertile afkom efter en parring mellem en hun ged og et han
får, hvorimod fostrene dør i den omvendte kønskombination. Drægtighedstidens længde
er næsten identisk for får og ged ca. 148 dage.
Mink har kun 30 kromosomer, se næste afsnit eller her. Der er en vis lighed mellem mink og katte kromosomer.
De to rævearter, der findes på de danske pelsdyrfarme, rødræv og blåræv har
henholdsvis 34 og 50 kromosomer. Rødræv har kun metacentriske kromosomer og udover
de almindelige 34 kromosomer har de fra 1 til 5 mikrokromosomer, betydningen
af mikrokromosomerne er ikke kendt. Blåræven har 2 par acrocentriske kromosomer
og alle de øvrige er metacentriske.
Der kan forekomme nonfertile afkom efter en parring mellem de to rævearter.
Drægtighedstidens længde er næsten identisk for de to arter ca. 58 dage.
Denne krydsning har til tider været meget populær i pelsproduktionen.
Hunden har 78 kromosomer, der bortset fra kønskromosomerne alle er acrocentriske.
Heste har 64 kromosomer og æsel har 62, og der kan produceres ikke fertilt afkom efter parring mellem hest (mor) og æsel (far). Denne krydsning kaldes et muldyr.
Hønsenes kromosomer ligner kromosomer fra de fleste fugle og krybdyr. Der er 6 par kromosomer, der minder om pattedyr kromosomer, og mange såkaldte mikrokromosomer, 2n= 78. Kønskromosomerne er blandt de største kromosomer, de betegnes som ZZ hos hanen og ZW hos hønen, hønsekromosomer se her.
Når der arbejdes med kromosomkortlægning vil man gerne kunne placere et gen på et bestemt sted på kromosomet, for hver art er der derfor lavet en standard med nummerering af de enkelte bånd på hvert enkelt kromosom. For denne nomenklatur har man også vedtaget at kalde den korteste kromosomarm for p-armen og den længste for q-armen. Ved opsætning af kromosomer vender q-armen altid nedad. Bånd numrene går fra centromeret ud mod telomerene.
Såfremt et individ ikke har et balanceret kromosomsæt med to kromosomer i hvert par, vil det normalt give sig til kende på dyrets phenotype med afvigende egenskaber. Og dyr med et ubalanceret kromosomsæt vil almindeligvis være sterile og ofte med nedsat livskraft. Dyr der har et balanceret kromosomsæt vil være phenotypisk normale. Kromosomfejl hos dyr med normal phenotype bliver normalt opdaget ved at f.eks. en tyr har alt for lav fertilitet, karyotypen fra en sådan tyr er vist i figur 10.2.
Kvægkromosomer 2n=60,XY, farvemetode BrdU indkoporation - Acridin Orange, Translokation 1/8. Christensen, K., Agerholm, J.S. & Larsen, B. 1992a. Dairy breed bull with complex chromosome translocation: Fertility and linkage studies. Hereditas 117, 199-202.
| Figur 10.2
Kvæg translokation mellem kromosom 1 og 8. |
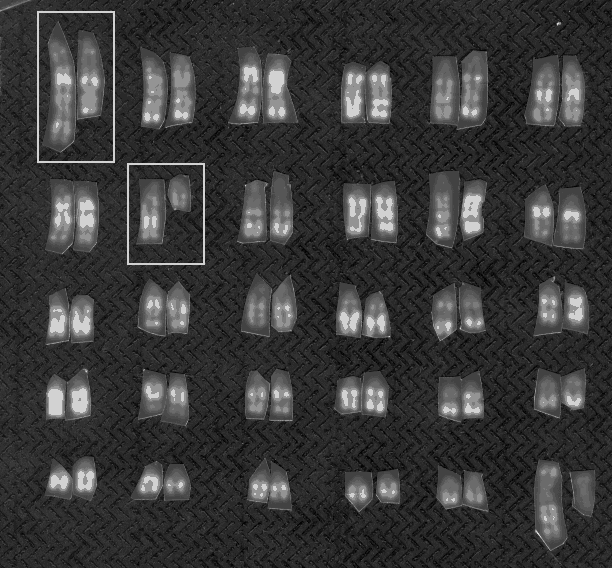 |
Normalt aborteres dyr med trisomi 28, men enkelte dør omkring fødselstidspunktet.
Hos mange af vore husdyr findes mindre grove kromosomfejl. De består
eksempelvis i at to acrocentriske kromosomer fusionerer. Dette kaldes en
centric fusion.
Den mest kendte er 1/29 centromer fusion mellem kromosom 1 og 29
hos kvæg. Når en sådan fusion forekommer i heterozygot
form, giver den anledning til svagt nedsat fertilitet, i størrelsesorden
af 10 procent, når det drejer sig om omløberprocent.
En tilsvarende centromerfusion findes hos blåræve, og her er effekten af samme størrelsesorden, når det drejer sig om kuldstørrelse, se nedenstående tabel, hvor kromosomtallet 49 svarer til en heterozygot med hensyn til centromerfusion. Data fra Christensen et al. Hereditas 1982, 97:211-215.
Tæve kromosomtal Antal kuld Kuldstørrelse 48 16 11,9 49 42 9,8 50 17 11,2 Fædre kromosomtal 48 10 12,2 49 52 10,1 50 13 11,2Metafaser fra de tre typer er vist i figur 10.4, og der er sat en cirkel om de kromosomer, der indgår i centromerfusionen.
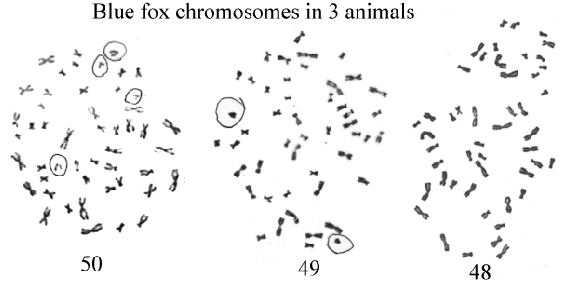
Hos mus er kendt individer, der har op til 7 centromerfusioner. Disse
mus har, når alle fusionerne forekommer i heterozygot form, meget
stærkt nedsat fertilitet.
Figur 10.4a. Udspaltning af kromosomer fra centromerfusions heterozygoter resulterer i nondisjunktion og uniparantal disomi. 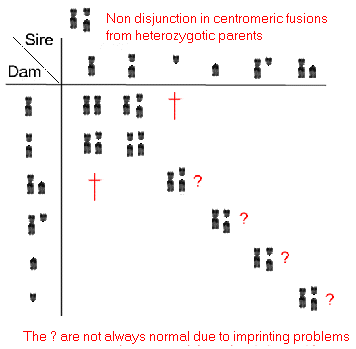 |
Tyrekvier: Kromosomundersøgelse kan anvendes til at påvise
sammensmeltning af de placentale blodbaner
hos tvillinger af forskelligt køn hos kvæg. Sammenblandingen giver sig udslag i,
at der kan etableres stamceller for hvide og røde blodlegemer fra begge dyr med proportioner
gående fra 0 til 100 procent af den rigtige 'type'. Er der for stor en sammenblanding
giver det anledning til at kviekalven får misdannede kønsorganer 'en tyrekvie' og dermed bliver
infertil. Tyrekalven har normal fertilitet, men i forbindelse med faderskabssager, der
normalt gennemføres på blodprøver, får man på grund af kimerismen
ikke entydige resultater.
Ved blodprøvetagning til faderskabssag bør det derfor oplyses, såfremt kalven er en tvilling.
Figur 10.5. Heste kromosomer 64, XX
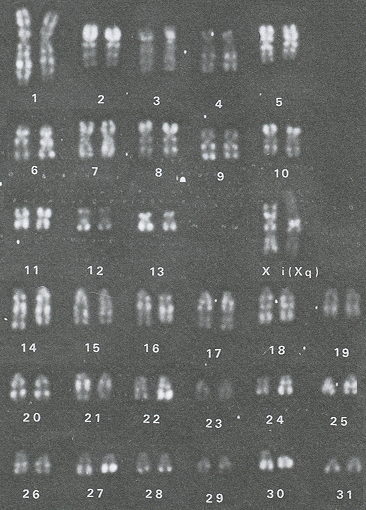 |
Auli Mäkinä, ved universitetet i Helsinki har en god oversigt over kromosom afvigelse hos hest.
Celler der dyrkes i to cycler, med BrdU tilsat i første cyklus,
kan afsløre fænomenet SCE (sister chromatide exchange). SCE
kan identificere individer med ustabile kromosomer eller anvendes til mutagenitetstest,
idet antallet af SCE er proportional med dosis af mutagenet. Nedenstående
er vist mink kromosomer, der udviser SCE eller Harlekin kromosomer. De
kromosomer hvor der ikke har været nogen SCE udviser på kromosomet
to ubrudte strenge en lys og en mørk, hvor der er SCE skifter strengen
farve. For at der kan ske SCE må der nødvendigvis have været
et brud på DNA'et på begge strenge.
| Figur 10.6.
Mink kromosomer 30 XY, der viser sister chromatin exchange |
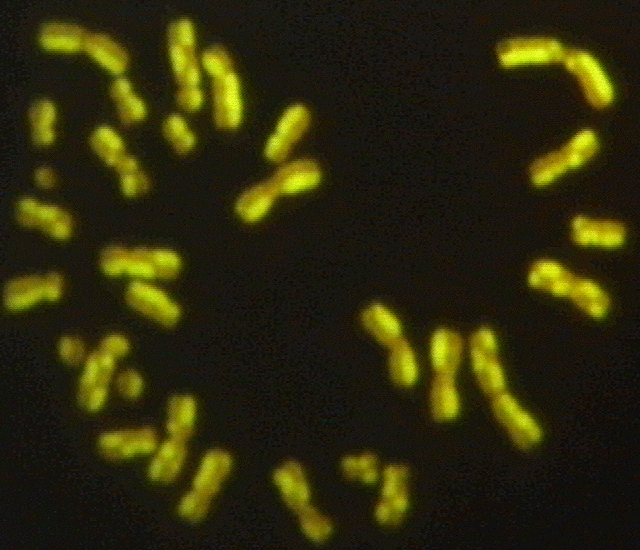 |
I figur 10.7 er vist et paint på grisekromosomer med DNA fra en hamstercellelinie der indeholder p-armen af grisekromosom 12. To kromosomer er painted, det er de identiske stykker på de to homologe kromosomer.
| Figur 10 7.
Paint på grise kromosomer med p-armen af kromosom 12 |
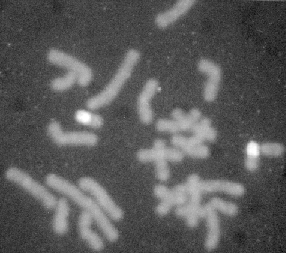 |
Paint metode er i store træk følgende (Fluorescens in situ hybridisering, FISH):
Når der paintes med et mindre stykke DNA, f.eks. et 40 kb stort insert i en cosmid, fås meget distinkte resultater i form af 2 pletter, en på hver af de to kromatider på de to homologe kromosomer se her.
Link her for at se billede af kromosom-paint med humane kromosomer. Alle de humane kromosomer er sorteret, så man kan købe rent DNA fra alle enkelte kromosomer. Når de mærkes op forskelligt, får hvert kromosompar sin egen farve. Denne teknik gør det til en enkelt sag at identificere de kromosomer, der er involverede i komplekse translokationer.
Ved hjælp af kromosom-paint kan der identificeres homologi mellem arter, se Figur 10.8 med minkkromosomer (til venstre), og de samme kromosomer (til højre) er hybridiseret med human kromosom 14. En tabel over homologien mellem kromosomerne hos 4 husdyrarter og mennesker er vist her
| Figur 10 8.
Paint på mink kromosomer med humant kromosom 14. I venstre side er der DAPI farvede kromosomer til identifikation mens højre side viser paintet, der er på p-arm af kromosom 13. |
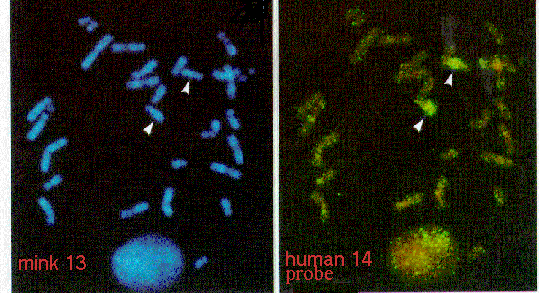 |
Et normalt individ der er bærer af en balanceret translokation, vil producere kønsceller der er normale og kønsceller hvor translokationen giver anledning til non-disjunktion af de homologe kromosomer med produktion af kønsceller med afvigende kromosomtal til følge.
I 10.9 figur er vist histogrammer fra flow-cytometri på sædceller fra orner. Histogrammet repræsenterer en flouroscens aktivitet, der er proportional med sædcellens DNA-indhold. Hvert histogram omfatter ca. 3000 sædceller. Ornen til højre (nr. 1130) er normal, den producere sædceller med et Y- og med et X-kromosom i forholdet 1:1. En sædcelle der indeholder et Y-kromosom har ca. 4 procent mindre DNA end en sædcelle der bærer et X-kromosom. Dette afspejles i at der er to fordelinger hvis middelværdi er 4 procent enheder forskudt.
Ornen til venstre (nr.1523) er bærer af en translokation mellem kromosom 1 og 17. Når denne orne danner sædceller, vil der ske fejl med hensyn til disse to kromosomer. Kromosom 1 er et meget stort kromosom der repræsenterer ca. 9 procent af en sædcelles DNA. Derfor ses der i denne ornes histogram to ekstra toppe symmetrisk en på hver side. Den lille ekstra top til højre svarer til sædceller med to kromosom 1'er, mens toppen til venstre svare til sædceller med intet kromosom 1. De to ekstra toppe kommer kun frem henholdsvis sammen med et X- og sammen med et Y-kromosom. Et ekstra eller tab af kromosom 17 er ikke direkte synligt, da dette kromosom er et lille kromosom, med omkring 2 procent af sædcellens DNA-indhold.
Undersøgelserne er publiceret af Jensen, P.O. et al. 1993. Proceedings of 10th European Collequium on Cytogenetics of Domestic Animals pp 104-108.
| Figur 10.9. Flow cytometri af grise sædceller indfarvet med DAPI. Normal dyr har to toppe en for X og en anden for Y bærende celler. Dyr med translokationer udviser flere toppe på grund af fejl under meiosen (non-disjunktion). |
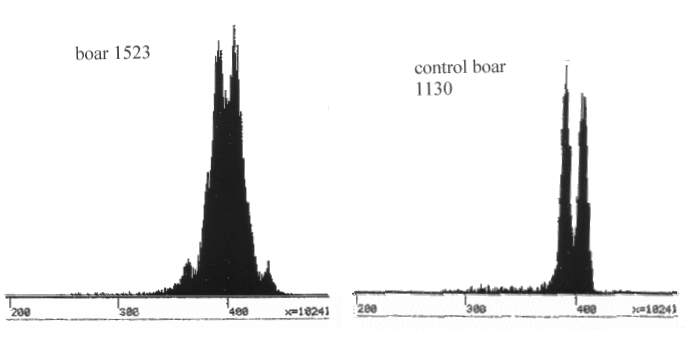 |
Der er naturligvis også en vis interesse for at anvende flow-cytometrien præparativt, så man på den måde kan få sædceller der bærer Y-kromosomet eller X-kromosomet i ren form. Alle pattedyr arter har en relativ forskel i DNA indhold mellem Y- og X-bærende sædceller af samme størrelsesorden på mellem 4 og 4,5 procent. Teknisk er det muligt at arbejde med en variationskoefficient (CV) på ca. 1 som i ovenstående eksempler fra svin.
Hidtil er resultaterne med hensyn til levende afkom efter befrugtning med kønssorterede sædceller kun på det eksperimentelle stade. Flow-cytometrien lader sig p.t. kun gennemføre efter indfarvning med flourokromet DAPI, efter at sædcellerne er behandlet med papain. Papain-behandlingen er nødvendig, for at der kan ske en ensartet indfarvning med DAPI.
Kromosomspecifikke DNA-prober til påvisning af non-disjunktion i sædceller
En anden metode til påvisning af non-disjunktion kromosomfejl benytter sig af stærke kromosomspecifikke prober. Efter in situ hybridicering til udstrygningspræparat af sædceller og efterfølgende påvisning af tilstedeværelse af signal, er det muligt at påvise sædceller med 0, 1 (normal) eller 2 af det pågældende kromosom, afhængigt af antallet af positive hybridiceringsområder. Undersøgelser fra mennesker giver skøn for non-disjunktion-fejl i sædceller, der ligger i størrelsesorden 5-8 procent. Dette svarer til en fejlprocent på ca. 0,2 for hvert kromosompar.
Udvikling af DNA prober til sådanne undersøgelse hos husdyr er p.t. i sin vorden. Eksempler fra anvendelse på minksædceller kan ses her.
1. Alment om hårtyper hos pattedyr
2. Alment om farvetyper hos pattedyr, farvegener
3. Farvegenernes biokemiske funktion
4. Farvegener i de forskellige husdyrarter
- Lyd og billed show (real player should be installed) eller Billed show
Hår og hårets farver er vigtige for dyrs overlevelse i naturen. Her beskrives
en del hårkarakteristika og der gives en mere detaljeret beskrivelse af arveanlæg
der indgår i melaninsyntesen. Melaninkorn er grundlaget for hårets farve.
De vigtigste farvegener beskrives, såvel som deres udbredelse indenfor de enkelte
arter og i de danske husdyrbestande.
-------
Håret hos pattedyr kan dels karakteriseres ved dets længde og dels ved dets fysiske
beskaffenhed såsom glat kontra krøllet. Forholdet mellem dækhår og underuld spiller ligeledes
en stor rolle for hårets fysiske egenskaber. Endelig er der farven, som er med til at give
dyret kamuflage eller ved stærke farver dominans over for andre artsfæller.
For de pattedyr der lever i vand eller ernærer sig ved jagt på dyr der lever i vand, er pelsen
af stor betydning for varmereguleringen. Pelsen skal også have stor slidstyrke
for at holde igennem hele vinterperioden, af eksempler kan nævnes sæl, odder og mink.
Harer og ræve har også en varm pels, men den har hos disse dyr ikke nær samme
slidstyrke. Hos de fleste pattedyr produceres der en vinterpels i oktober-november, der
erstattes af en sommerpels i april-maj.
Visse af de fysiske egenskaber styres af simpel Mendelsk arvegang, man har feks:
Hårtyper og genotyper
Dominant Recessiv --------------------------------------- Ruhåret W- Glathåret ww Korthåret L- Langhåret ll Dækhår M- Mole mm Hår Hr- Hårløs hr/hr ----------------------------------------
I figur 11.1 er vist eksempler på de forskellige hårtyper.
| Figur 11.1.
Den ruhårede Airdale terrier |
 |
| Langhårede type hos gravhund. |  |
| Pelsen fra en mole mink og en normal Standard mink anno 1965. |  |
| Hårløs mus. |  |
Hårets farve bestemmes af dets indhold af melaninkorn. De sort brune farver skyldes eumelanin og de gul røde farver skyldes phæomelanin. Sidstnævnte er opløseligt i saltsyre. Såfremt der ikke er indlejrede melaninkorn bliver håret hvidt, dette skyldes indlejrede luftblærer, der giver hvid farve, ligesom luft i eller under is giver den hvide farve.
Melanin dannes ud fra aminosyren tyrosin gennem en lang række biokemiske processer. Hver af disse processer kan øve indflydelse på dyrets farvetype. Melaninet dannes i en celletype der kaldes melanocytter. Antallet og den hormonale styring af disse celler kan ligeledes give anledning til farvevariation.
I figur 11.2 er anført en liste over de mest kendte farvegener.
| Figur 11.2
Agouti locus (A locus) |
||
| Dominant Yellow Ay- Dominant Black A- Recessiv Black and tan at- Recessiv Yellow aa |
Aierdale terrieren på foregående side har genotypen Black and tan atat, sort på ryggen og tan farve på bug og lemmer. | |
| Brown locus (B locus) | ||
| Dominant Black B- Recessiv Brown bb |
 Brown genotypen bb forekommer hos mange hunderacer |
|
| Albino locus (C locus) | ||
| Dominant Farve C- Recessiv White cc |
 Albino genotypen cc med røde øjne hos en Angora kanin |
|
| Dilution locus (D locus) | ||
| Dominant Black D- Recessiv Silver dd |
 Silver genotypen forekommer også hos grise |
|
| Extension locus (E locus) | ||
| Dominant Sort E- Recessiv Yellow ee |
 |
|
| Pink eyed dilution locus (P locus) | ||
| Dominant Black P- Recessiv Yellow pp |
||
| X-linked Orange locus (O locus) | ||
| Females: Dominant Black oo Heterozygot Black/Yellow Oo Recessiv Yellow OO Males: |
 Heterozygoten Oo har en blandingsfarve på grund af den tilfældige X-kromosom inaktiveringen. Blandingsfarven kan variere fra en næsten perfekt blanding til store pletter af gul og sort afhængigt af hvornår den tilfældige inaktiveringen sker. |
| Figur 11.3.
Somatisk mutation i gen for farve, hele øret hos en Shadow ræv har farve. Shadow ræve er normalt flødefarvet overalt på kroppen. |
 |
I figur 11.4 er vist en melanocyt. Der er i figuren antydet nogle af melanocyttens funktioner og hvorledes de påvirkes af farvegenerne, der er nævnt i foregående afsnit.
MSH eller melanocyt-stimulerende hormon bliver produceret i hypofysen. Dette hormon
er vigtigt for produktionen af melanin. MSH-receptoren svarer til e-locus,
hvorimod en blokker af dette hormon svarer til a-locus.
| Figur 11.4. Viser funktionen af de 5 mest kendte farvegener hos pattedyr. Hårfarven skyldes de melaninkorn melanocyten danner. |
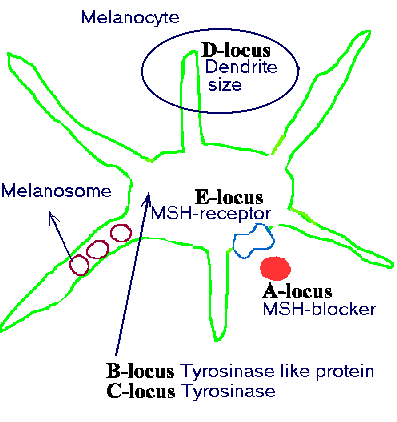 |
På b og c locus bliver der kodet for 'enzymer', der sørger for omlejring af aminosyren
tyrosin, tyrosinase. Omlejringen er nødvendig for at der overhovedet kan dannes melanin.
Locus d har med dendrit-størrelsen at gøre.
Når man sammenligner genernes kendte alleler giver det mulighed for at tænke på en fortolkning af funktionen. Feks kan der både være en dominant og en recessiv gul i forbindelse med agouti locus. At der vil være en stærk afhængighed mellem effekten af a og e locus er ganske indlysende, da de påvirker samme system, MSH funktionen.
Melanocytternes udbredelse i hårlaget er også en vigtig faktor for hårets farve. Som eksempel skal nævnes to genpar der kendes fra mus, steel (sl) eller (Mast cell growth factor=Mgf) og white spotting (Kit genet), der er Mgf receptoren. Disse to gener er med til at styrer udbredelsen af melanocytterne i huden, og kan som navnet på det ene genpar antyder give anledning til hvide pletter. Er der færre melanocytter i hårlaget får man ofte en blanding af farvede og hvide hår, denne effekt kan styres fra steel lokus.
Hos mus er kendt op mod 100 farvegener, de kan alle henføres til en af de neden nævnte kategorier
Gener der indgår i melanin syntesen Gener der (regulerer) styrer melanin produktion Gener der vedrører antallet af melanocytter Gener der styre melanocyttens morfologiFlere detaljer og referencer vedr melanin syntese.
Modifikation af farvetonen kan ske ved klassisk selektion, hvor farvetone behandles som en kvantitativ egenskab. Hos mink er vild mink farvetypen mørkebrun. Ved selektion for mørkere farve er der gennem selektion over ca 25 generationer skabt en mink type, der er kulsort.
Milieuets indflydelse på udbredelsen af feks. hvid farve kan tydelig ses ved kloning, hvor der er ret stor forskel på individer med identisk genotype. Se her med billeder af identiske katte, Nature 2002 vol. 415 side 859.
Nedarvning af farver hos de danske svinracer er styret af følgende tre loci, se også figur 11.5.
Dominant Recessiv ----------------------------------------------- Dominant hvid I- Farvet ii Hvidt bælte i(Be)- Ensfarvet ii Sort E- Rød ee ------------------------------------------------
Landrace (L) og Yorkshire (Y) racerne er hvide, og er homozygotiske for dominant hvid.
Duroc (D) racen er rød.
Hampshire (H) racen er sort med hvidt bælte.
| Figur 11.5
Landrace (L) og Yorkshire (Y) racerne er hvide, og er homozygotiske for dominant hvid. Duroc (D) racen er rød. Hampshire (H) racen er sort med hvidt bælte. |
 |
De fleste produktionsgrise i Danmark har en LY mor og en farvet far (D eller HD). De er alle hvide da de er heterozygotiske med genotypen Ii. Marklund et al. 1998, Genome Res 8:826-33, har påvist at dominant hvid hos svin skyldes alleler i det såkaldte kit gen, der svarer til mast cell growth factor receptoren. Bælte genet er beskrevet i Mamm Genome 1999 Dec;10:1132-6 af Giuffra et al..
Nedarvning af farver hos de danske kvægracer er styret af følgende tre loci.
Dominant Recessiv --------------------------------------- Sort E- Rød ee Ensfarvet S- Broget ss Hvidt hoved SH- Ensfarvet SS ----------------------------------------
Sortbroget dansk malkerace (SDM) har genotypen EEss og
Rød dansk malkerace (RDM) har genotypen eeSS.
Krydsninger mellem SDM og RDM giver ensfarvet sort afkom. Enkelte RDM har farvetegningen
tigerstribet, det er en allel i e locus, der er dominant i forhold til rød.
Hos en del kødkvægsracer
feks. Hereford forekommer farvetegningen hvidt hoved, der har dominant nedarvning, den
nedarves fra en dominant allel i samme lokus som brogethed. Det vides, at genet for brogethed
ligger på kromosom 6, og det er tæt koblet til kit genet og har interaktion med dette.
| Figur 11.6.
Sortbroget dansk malkerace (SDM) har genotypen EEss og Rød dansk malkerace (RDM) har genotypen eeSS. Hereford har farvetegningen med hvidt hoved, der har dominant nedarvning.  |
Klungland et al. 1995, Mamalian Genome 6:636-39, har påvist at rød farve hos kvæg skyldes ee genotypen i extension locus.
Nedarvning af pelsfarver hos hund, af Helle Friis
Proschowsky
Nedarvning af farver hos hunde er meget komplekst, og det følgende bliver derfor kun
en kort beskrivelse. Hver race har sit specielle særpræg, og interesserede henvises til "
bibelen" på dette område: "The inheritance of coat colors in dogs"
af Clarence C. Little,
Howell Book House, 1984.
Farven i hundes pels skyldes pigmentkorn der indeholder stoffet melanin. Størrelsen og
tætheden af kornene afgør hvor mørk pelsen ser ud. Pigmentkornene dannes kontinuerligt ved roden af håret mens det gror. Hvis denne proces ændres eller afbrydes når håret
er vokset halvt ud, fås et bånd af en anden nuance på håret. Dette kaldes vildtfarve eller
agouti, og findes bl.a hos Schæfer og Norsk elghund. Vildtfarvede hvalpe fødes sorte,
fordi kun den første del af håret er vokset frem ved fødslen.
Man mener at der findes loci (steder) for farvegener på mindst 10 forskellige kromosompar hos hunde. Alle hunde besidder disse farvegener, men langt fra alle alleler kommer
til udtryk i alle racer.
Hos nogle racer er pelsfarven meget konstant, og alle individer i racen har i princippet
samme farve, som f.eks. Rottweiler. Hos andre findes et utal af farvevarianter.
Kort beskrivelse af de mest kendte loci´s betydning for farven:
Locus A: Bestemmer mængden og lokaliseringen af mørkt og lyst pigment, både i det
enkelte hår, og i pelsen som helhed. Allelen at giver f.eks. black and tan- farve hos
Rottweiler, Airdale og Gordon setter.
Locus B: Bestemmer om mørkt pigment skal være sort (B)
eller leverbrunt (b).
Locus C: Bestemmer pigmenteringsdybden. Indeholder bl.a. allelen
ca der giver
albinoer og chinchilla-allelen cch , der lysner røde
og gule farver til cremefarvet hos
feks Cocker spaniel. Chinchilla-allelen er også
årsag til den store variation i pigmenteringsdybden hos f.eks.
Cheasapeake bay retriever og Tibetansk terrier.
Locus D: Påvirker intensiteten af farven. Allelen store D giver intens farve (sort Grand
Danois) mens allelen d giver blå fortynding. Weimaraner har altid allelen d sammen
med b, det er altså leverbrun der bliver fortyndet til den karakteristiske
farve.
Locus E: Påvirker mønstret af mørkt pigment i pelsen.
Allelen Em giver f.eks. sort
maske hos Leonberger ,og allelen ebr er ansvarlig for tigerstribning
( brindle) hos Boxer
og Grand Danois, mens genotypen ee giver gul farve hos Labrador retrievere.
| Figur 11.7
Black and tan- farve hos Airdale, atat, Dilution farven hos Tibetaneren, dd, og gul farve fra Extention hos Labrador retrievere, ee.  |
Nedarvning af pelsfarver hos kat, af Nan Hampton, University of Texas at Austin, der også har et flot power point show på 50 billeder.
The following is a table of some of the more common genotypes and phenotypes of the domestic cat.
| Common Genotypes and Phenotypes | |||||
| Homozygous | Homozygous | Heterozygous | |||
| Genotype | Phenotype | Genotype | Phenotype | Genotype | Phenotype |
|---|---|---|---|---|---|
| AA | agouti | aa | non-agouti (black) | Aa | agouti |
| BB | black pigment | bb | brown pigment | Bb | black pigment |
| CC | full color | cbcb cscs |
burmese siamese |
Ccb Ccs cbcs |
full color full color tonkanese |
| DD | dense pigment | dd | dilute pigment | Dd | dense pigment |
| ii | full pigment | II | pigment limited to tips of hair, base of hair light gray or white, agouti especially affected with agouti=silver tabby with non-agouti=smoke with orange=cameo |
||
| LL | short hair | ll | long hair | Ll | short hair |
| mm | long tail | MM | prenatal lethal | Mm | short tail |
| oo or oY | non-orange (usually black) | OO or OY | orange | Oo | tortoiseshell=orange and black in females |
| ss | no white spots | SS | white spots > 1/2 body | Ss | white spots < 1/2 body |
| TT | mackerel stripe | TaTa tbtb |
Abyssinian blotched |
TTa Ttb Tatb |
Abyssinian, faint leg and tail stripes Mackerel stripes Abyssinian, faint leg and tail stripes |
| ww | not all white | WW | all white | Ww | all white |
| Colour types, single | Mutant name | Mutant genotype | Wild type, Standard |
| White | Albino, red eyed | cc | CC |
| Hedlund White, deaf | hh | HH | |
| Grey | Aleutian, bluish | aa | AA |
| Silver Blue, grey | pp | PP | |
| Steel Blue | psps | PP | |
| Brown | Royal Pastel | bb | BB |
| Moyl | mm | MM | |
| American Palemino | kk | KK | |
| Bicoloured | Black Cross | Ss | ss |
| 95 % White | SS | ss | |
| Finn Jaguar | Zz | zz | |
| Combinations | |||
| Bicoloured | Pastel Cross | bb Ss | BBss |
| Bluish grey | Sapphire | aa pp | AAPP |
| Blue Iris | aa psps | AAPP | |
| Sand | Pearl | mmpp | MMPP |
| Light sand | Violet | aakkpp | AAKKPP |
The following three crosses (F1) are commonly used to produce the glow type
Sapphire x Pastel Pearl x " Violet x " F1 x Wild mink
References: Experience from farm praxis.
Nes, N., et al. 1988. Beautiful
Fur Animals and their Colour Genetics. Scientifur, 60 Langagervej, DK-2600
Glostrup.
Below is shown mink colour types from the book Beautiful Fur Animals, with permission from Outi Lohi.

Farvegener hos heste
For en detalieret beskrivelse af hestens farvegener henvises til hestens farvegenetik fra the Model Horse Reference website, Horse Colours Genetics. eller fra the Veterinary faculty in Davis, California Horse Colours
De vigtigste farvegener hos hest med angivelse af baggrunds farvegener :
| Agouti locus (A locus) | Baggrund B-CCEE | ||||
| Dominat brun, A- |  |
Recessiv sort aa |  |
||
| Brun (B locus) | Baggrund aaCCEE | ||||
| Dominat sort, B- |  |
Recessiv rødbrun, bb |  |
||
| Cremello locus (Cr locus) | Baggrund aaee | ||||
| 'Dominat' rød, CC |  |
Heterozygot, CCr |  |
'Recessiv' lys, CrCr |  |
| Extension locus (E locus) | Baggrund aaB-CC | ||||
| Dominat sort, E- |  |
 |
Recessiv rød, ee |  |
|
| Grå locus (G locus) | Baggrund AAB-CCEE | ||||
| Dominat grå, G- |  |
Recessiv brun, gg |  |
||
| Skimmel locus (R locus) | Baggrund AAB-CCEE | ||||
| Heterozygot skimmel Rr |  |
Recessiv brun, rr |  |
Dominant RR, dør | |
| Dominant white (W locus) | Baggrund AAB-CCEE | ||||
| Heterozygot hvid Ww |  |
Recessiv brun, ww |  |
Dominant WW, dør |
Farvegenerne virker i et samlet hele, de ovenfor viste typer
er stiliserede, i den virkelige verden er der jævne overgange mellem farvetyperne
på grund af modificerende gener.
Generne i agouti og extension lokus arbejder som tidligere omtalt sammen,
så skal en hest være sort skal den have genotypen aaE-; en aaee hest er rød.
Der er også sammenspil mellem de øvrige farvegener.
Skimmel og ekstension lokus er koblede.
Locke et al. (2001)
Animal Genetics 32:340-343, har
vist, at cream dilution Cr allelen ikke sider i C locuset
som tidligere anført med gensymboler.
Genet ikke er homologt med tyrosinasegenet i andre arter.
Marklund el al. Mamm Genome 1999;10:283 har vist at skimlet genet svarer til
kit genet (mast cell growth factor reseptoren).
Rieder et al. Mamm Genome 2001,12:450 har vist at den sorte phenotype svarer til
en recessiv allel i agouti genet. Og at den brune farve skyldes en allel i extension locus.
Andre arter
For en detaljeret beskrivelse af kaninens farvegener og farvetyper henvises til Jackie Carey's Rabbit Color Genetics
1. Beregningsteknologi for avlsværdi skøn
2. Kunstig sædoverføring, betydning for beregning af avlsværdi skøn, og sexing af sæd
3. Transgenese og transgene dyr
4. Anvendelse af DNA-markører for sygdomsgener
5. Påvisning af DNA-markør koblet til sygdomsgener eller QTL'er
6. Resultater af selektionsforsøg for forbedret sygdomsresistens
- Lyd og billed show (real player should be installed) eller Billed show
Der gives en oversigt over de teknologiske forhold, der anses som relevante
for husdyravlen. 'Animal model' avlsværdiskøn beregnes samtidig for alle individer
i en population, hvor alle samtidig bidrager med information om hinanden.
Effekt af reproduktions-teknologi såsom kunstig sædoverføring har stor indflydelse
på avlsværdivurderingen og dermed på avlen, hvorimod kønssortering af sæd og
overførsel af embryoner i de fleste tilfælde kun har marginal betydning.
Transgenese og kloning bliver også omtalt. Der gives en oversigt over anvendelse
af DNA-markører for kvalitative og kvantitative egenskaber. Og der gives en ret
udførlig gennemgang af muligheder for avl for bedre sygdomsresistens hos husdyr.
-----
Der er i lektion 7 gennemgået metoder til beregning af avlsværdi skøn
i forbindelse med data fra slægtninge med ensartede slægtskabsforhold.
Dette er den simpleste form for avlsværdivurdering,
da den ikke kræver meget regnekraft, fordi
den er baseret på beregning af en enkelt vægtfaktor,
der er afhængig af antal og et gennemsnit
af en gruppe målte individer med indbyrdes ensartede
slægtskabsforhold, feks en afkomsgruppe bestående af halvsøskende.
Med indførelse af stadig kraftigere
computere, er der skabt basis for at udnytte data
langt mere effektiv i forbindelse med avlsværdi
bestemmelse. Metoderne er baseret på lineære
ligningssystemer, hvor hver observation i princippet får
en ligning. Der kan derved dannes et ligningssystem
til beregning af vægtfaktorer for den enkelte
observation. I modellen medtages der alle
observationer fra slægtninge og dyret selv, tillige
med observationer fra slægtninge til slægtninge.
Eksempel på slægtninge til slægtninge er
moderen til et afkom hvor faderen vurderes eller
omvendt.
Er moderen til afkommet med i modellen for faderens avlsværdi,
forsvinder kravet om tilfældig parring,
da der korrigeres for mødrenes eventuelle afvigelse fra populationsgennemsnittet.
Kravet til at alle observationer skal foregå under
samme milieuforhold får mindre betydning, ved
feks. at lade besætningsgennemsnit indgå i beregnings
modellen og tillige stille krav om, at mere end en
familie skal være repræsenteret pr. besætning.
De vigtigste beregningsmetoder for avlsværdi skøn:
1. Selektions index (SI)
2. Best linear prediction (BLP)
3. Best linear unbiased prediction (BLUP)
4. Animal model (AM)
5. Multitrait nimal model (AM)
6. Genomisk selektion
Selektionsindekset blev udviklet i 1950'erne
og har været anvendt før computer alderen. SI bruges
stadig til modelberegninger, især fordi den er velegnet
til at inddrage flere egenskaber og giver et forventet
delta G (genetisk ændring) for hver egenskab, såfremt man anvender et bestemt
sæt af økonomiske vægtfaktorer. SI svarer til modellerne der er beskrevet i lektion 7 og 8.
Før computer alderen var det almindeligt at prækorrigere
data for f.eks. kælvealder eller slagtevægt, idet der
altid vil være en vis biologisk variation for disse egenskaber.
Prækorrektion af data anvendes fortsat i en vis
udstrækning.
Med fremkomst af computerne var
det nærliggende at udvikle
modeller, der samtidig beregnede avlsværdi for samtlige
dyr i en population. Når dette var tilfældet var det
lettest også at anvende alle informationer, således at
alle individer var informative i forbindelse med alle andre.
BLP inddrager ikke milieufaktorer, hvilket gør den mindre
anvendelig. BLUP og AM inddrager samtidig estimation
af milieueffekter og korrigere for dem.
I de tre sidstnævnte metoder indgår slægtskabsmatricen
som vist beregnet efter tabularmetoden i lektion 4.
Løsning af de mange ligninger kan ikke ske eksplicit,
som man har lært i forbindelse med løsning af to ligninger
med to ubekendte. Løsningerne er baseret på forhånds
gæt og derefter gennemløb af alle data med forbedring af gættet
indtil estimaterne bliver stabile efter næste gennemløb.
Denne metode
kaldes iterativ. Med denne metode kan man bestemme
avlsværdier for millioner af dyr samtidig. AM metoden
anvendes for nuværende i både dansk kvæg- og svineavl for
de vigtigste egenskaber.
Genomisk selektion af Thomas Mark
Genomisk selektion er en ny teknologi, hvor avlsværdi forudsiges udfra
genom-dækkende markører i form af enkelt nucleotid polymorfier SNP'er. Det
genetiske kort er baseret på SNP'er, og de giver os mulighed for at opdele
hele genomet i tusindvis af forholdsvis små kromosom segmenter. Så effekten
af hvert kromosom segment estimeres samtidigt. Endelig er genomiske avlsværdier
lig summen af alle forventede kromosom segment effekter. Kromosom segment
effekterne kan vurderes for en gruppe af dyr (dvs. en reference population), og
for de resterende dyr, er det kun nødvendig med en blod-eller vævsprøve for at bestemme dets
genomiske avlsværdi. Kromosomet segment effekter gælder også for alle dyr i
populationen, hvor de blev estimeret, fordi markørene er i koblingsuligevægt med det
kausale gen.
Ved hjælp af genom-dækkende informationer kan unge dyr præcis udvælgelse, forudsat at der er
fænotyper
fra tilstrækkeligt mange reference dyr. Det betyder, at genomisk avlsværdi er særligt
gavnligt, når de traditionelle valg er svært for eksempel når fænotype måling er
begrænset af køn og alder (fx meget nyttig for malkekvæg). Der tilrådes dog konservativ brug
af unge dyr uden fænotypisk information (om egen præstation eller afkom) for at undgå
potentielle negative bivirkninger relateret til ugunstige mutationer, ugunstige udvælgelse
pres på ikke-registrerede egenskaber i avlsmål og høj indavl.
Kunstig sædoverføring (KS) har naturligvis stor praktisk betydning, da man ved KS kan udnytte velafprøvede top dyr i en langt større udstrækning, end det er muligt ved naturlig parring. Der hvor KS virkelig får stor betydning er dog ved at finde frem til top avlsdyrene. Hvilke faktorer har da betydning i forbindelse med afprøvning af avlsdyrene, for at afprøvningen både er tilstrækkelig sikker og troværdig.
Vigtige forhold for beregning af avlsværdi skøn
1. Avlsværdi skønnet skal være tilstrækkelig sikkert bestemt
2. Avlsværdi skønnet skal være uafhængig af ejerforhold
3. Avlsværdi skønnene skal være sammenlignelige
I forhold til punkt 1 er det klart, at KS kan øge familiestørrelsen
og derved øge sikkerheden ved avlsværdiberegningerne.
For at punkterne 2 og 3 kunne blive opfyldt har det været
almindeligt at sende dyrene på teststation, derved blev
resultaterne uafhængige af ejerforhold tillige med
at resultaterne var sammenlignelige, da de var opnået under
de samme milieuforhold. Teststationerne har dog et problem
i forhold til punkt 1. Da stationerne er kostbare at drive,
må de nødvendigvis sætte en grænse for hvor mange dyr, der
kan afprøves. Det vil derfor gå ud over sikkerheden ved
afprøvningen, eller ved antal familier der kan afprøves.
KS kan løse problemerne med punkterne 2 og 3 samtidig med at
punkt 1 er bedst muligt tilgodeset, ved at kombinere KS med registrering
fra kommercielle besætninger.
Med KS opnås at de dyr, hvis resultater skal anvendes til
avlsværdi bestemmelse ikke kun findes i ejerens besætning, men
også i alle mulige andre besætninger. Samtidig vil der være afkom
efter alle mulige andre KS handyr i en
given besætning. Dette muliggør, at
der kan opnås sammenlignelige resultater for alle
KS handyrene samtidig,
ved at der anvendes afvigelser fra besætningsgennemsnitene
i stedet for at anvende absolutte præstationer.
det er da indlysende, at data fra besætninger hvor der kun anvendes en enkelt
tyr ikke er informative, da besæt.gns er lig tyr.gns.
For de dyrearter hvor KS endnu ikke er udviklet
eller hvor ejerne af handyrene
på en eller anden vis kan påvirke testets udfald, må der
af praktiske grunde fortsat anvendes teststationer. Teststationer
kan også komme på tale, hvor man ønsker at måle egenskaber, der er
vanskelige at måle hos den enkelte ejer som f.eks. foderoptagelse.
For kvæg og svin er KS så veludviklet at man stort set har
kunnet afvikle tidligere tiders afkomsprøvestationer. Man har dog
fortsat et lille supplement af data fra teststation for egenskaber,
man har svært ved at måle i praksis.
En anden fordel ved KS er at det er muligt at øge selektionsintensiteten
og dermed øge den genetiske ændring, jvf. lektion 8. Der skal anvendes
færre handyr, som i gennemsnit vil være bedre, sammenlignet med gns. af
en større gruppe, der skulle anvendes ved naturlig parring. Det samme
princip kan udnyttes i forbindelse med superovulation og ægtransplantation
for hundyrenes vedkommende.
For husdyrarterne høns, mink og ørreder er det fortsat
nødvendigt, at der for sammenlignlighedens skyld
anvendes teststation.
Den måde man anvender handyrene på indenfor heste og hundeavl
svarer stort set til anvendelse af KS. Her er der dog specielle
problemer med, at der er en tendens til, at de bedste handyr anvendes
sammen med de bedste hundyr, derved kan avlsværdibestemmelsen
blive biased, såfremt der ikke tages hensyn
til dette i forbindelse med avlsvædiberegningerne. Avlsværdi
er som den blev defineret i lektion 6 afhængig af
tilfældig sammenparring.
Ved at anvende avancerede beregningsmodeller til avlsværdi
beregningen, kan der dog tages højde for dette forhold.
Af andre uheldige forhold der kan påvirke avlsværdibestemmelsen
er forhold vedrørende indberetningen af uheldige resultater.
For HD hos hunde er det en stor fristelse, at undlade at indberette
HD positive hunde, da de alligevel ikke kan anvendes som avlsdyr.
En sådan bias i forbindelse med indberetningerne er det svært at
kompensere for ved avlsværdi beregninger, selv ved anvendelse
af de mest avancerede statistiske modeller.
Sexing af sæd
Det er muligt ved hjælp af præparativ flow sytometri at sortere sæd, så man kan
producere kviekalve eller tyrekalve efter ønske. Indenfor Jersey racen kan det ikke
betale sig at opfede tyrekalvene. Så her er der et stort ønske for at sætte
gang i produktion af den kønssorterede sæd.
Der er flere udenlandske firmaer der producere kønssorteret sæd. Men prisen
er p.t. for høj til stor praktisk anvendelse. Skal teknikken vinde bred
indpas indenfor husdyrproduktionen, må
teknikken vel også ændres - teknikken er p.t. baseret på anvendelse af flourokromer,
som indtil andet er bevist, må anses for at fremkalde mutationer med en vis frekvens.
Nærværende afsnit er kun tænkt som en meget kort opsummering.
Metoder til genoverførsel:
Efter transgenesen i ES eller andre føtale celler injiceres de transformerede celler ind i en blastocyst, og der dannes kimæriske individer, hvoraf nogle vil danne kønsceller, der er transgene. Succes raten med fosterudvikling uden støtteceller fra en normal blastocyst har været ringe, hvilket også må forventes på grund af problemer med at vedligeholde korrekt imprinting i celler der har gennemgået mange celledelinger efter zygote stadiet. Beskrivelse af imprinting fænomenet, se afsnit 10.3.
Genkonstrukter.
Et transgen skal normalt bestå af en promotor og et strukturgen.
Promotoren skal styre ekspression, hvornår og hvor meget, feks. skal
genet have ekspression i mælkekirtlen forsøges anvendt kasein
promotor, da det er et kendt mælkeprotein. Strukturgenet kan være med eller
uden introns. Stammer genet fra en bakterie er det altid uden introns,
fra eukaryoter kan genet være cDNA eller genomisk.
Produktionsmæssige motiver for transgenese.
Andre motiver for transgenese
Betegnelserne genmodificeret eller gensplejset bør hverken dække over en
god eller en dårlig proces.
Man har f.eks DNA strukturerne, der kaldes plasmider, der rask væk bevæger sig
mellem bakteriestammer og arter. Man må nødvendigvis anlægge de samme kriterier
for en vurdering af genets nytte- eller skadevirkning om genet er flyttet kunstigt
eller naturligt.
Disse plasmider er kendte i offentligheden, idet det er dem der fuldt berettiget er
årsagen til forbudet mod antibiotika i profylaktisk øjemed i dansk husdyrbrug.
Lægges der et selektionspres på mikroorganismerne vil de før eller siden opfange
resistens gener fra omgivelserne. Resistensen er baseret på at et gen koder for et
enzym, der kan ødelægge virkningen af et bestemt antibiotikum.
På tilsvarende måde kan tilførsel af et gen være en ønsket ting. Når genet som i
modificeret ølgær nedbryder et for smagen og konsistensen uønsket restprodukt fra
ølgæringen, synes vi alle, at det er fint. Især ølnydere værdsætter, at man bruger
en sådan gær.
Der er en lang række mikroorganismer, som bliver udnyttet i produktionen af levnedsmidler,
der med fordel vil kunne få tilført vel specificerede enkeltgener, hvorved man kan
forbedre smag, konsistens og holdbarhed i vore levnedsmidler.
Der findes også situationer hvor man ønsker at ødelægge et gen, da organismen lige
laver en biokemisk reaktion for meget.
Så genmodificeret eller gensplejsning som begreb dække hverken over gode eller
dårlige processer, politiker og administratorer gør os en dårlig tjeneste ved at
arbejde med så forsimplede begreber, når de i den offentlige
debat kun anvendes til at betegne noget odiøst. Gensplejsning kan anvendes til at lave
virkeligt gode og
nyttige ting, men de kan også anvendes til at fremstille organismer til
krigsførelse på den mest nederdrægtige måde.
DNA-markører indenfor familier
Sker der udspaltning af en recessiv sygdom indenfor en familie, og der foreligger
kendskab til sygdomsgenets placering på et kromosom tillige med flankerende DNA-markører,
er det indenfor familien muligt at påvise bærere af genet, selv om man ikke kender
den molekylær genetiske basis for selve sygdommen.
Metode: I figur 12.1 er vist DNA-markører A og B og et sygdomsgen (*). De to dyr i figuren er helsøskende og man har typet dem for generne A og B såvel som deres afkom. Blandt afkommet var der to syge med genotyperne AABB, på grundlag af de to syge afkom er forældrenes og de øvrige afkoms genotype m.h.t. sygdomsgenet og koblingsfaserne fastlagt.
| Figur 12.1. Genealogisk diagram med gamet typer på. Gamet typerne er deduceret på grundlag af test i laboratorium og udspaltning hos afkom mens sygdomsgenet er deduceret på grundlag af de to udspaltninger af syge individer. | |
Det femte afkom har en rekombination mellem sygdomsgenet og DNA-markøren B, idet den
har genotypen AaBB og ikke er syg.
For at DNA-markøren skal have nogen værdi, må
de dyr der udspalter for sygdomsgenet også være heterozygotiske for DNA-markøren.
Opsummering af undersøgelsen: Dyr med genotypen aabb er fri for sygdomsgenet,
hvorimod alle genotyper med mindst en allel af de store bogstaver må forventes at være
anlægsbære af
sygdomsgenet. Går man bagud i stamtavlen vil alle individer med mindst en allel
af de store bogstaver være mistænkt for at være anlægsbærer.
DNA-markører anvendt på populationsplan
Skal en DNA-markør anvendes på populationsplan må det baseres på at der er koblingsuligevægt.
Det vil der altid være såfremt at sygdomsgenet (mutationen) er opstået indenfor de seneste 10 til
15 generationer og markøren er tilstrækkelig tæt koblet, dvs afstanden mellem
markøren og sygdomsgenet må være mindre end 1 cM. DNA-markøren kan på populationsniveau
kun give en indikation for at et givet dyr har en højere chance for at være anlægsbærer.
Det endelige bevis for koblingen kan kun etableres gennem samtidig udspaltning af syge individer
og DNA-markøren indenfor familier.
Påvisning af DNA-markør generelt
Hos pattedyr og fugle er størrelsen af det samlede genom ca. 3000
centi Morgan (cM) eller rekombinationsenheder, der er dog en betydelig variation
mellem arter. De største kromosomer er to til tre hundrede cM lange,
mens de mindste er under 100 cM lange. Her er der også betydelig forskel
mellem de enkelte arter, hvor mink kun har 15 kromosompar og hunden
har 39. Hos pattedyr er der forskel på rekombinationshyppigheden mellem
hanner og hunner, det er således, at hunnerne har højere (10 to 20 %)
rekombinationshyppighed end hannerne, hvilket især gør sig gældende i områderne
omkring centromerene.
Tæt kobling er lettere at påvise end løs kobling,
afstande over 30 cM er i praksis næsten umulige at
påvise idet det kræver et meget stort antal informative
individer (500-1000). Det
er således, at kobling indenfor 10 cM kan påvises på grundlag af under
50 informative stk afkom fra en analysekrydsning.
For at man kan dække genomet regnes der med, at der
skal anvendes en DNA-markør for hver 20 cM, dette giver
ialt 150 DNA-markører, der skal types for at dække
hele genomet.
For at DNA-markøren kan anvendes skal den være informativ,
dette er for de fleste DNA-markører kun tilfældet i
50-70 procent af familierne, der skal analyseres. For at
få et komplet set af DNA-markører, må det derfor prescreenes
hos forældredyrene med op til 300 markører, for at få
et brugbart sæt på 150 til analyse af en given familie.
Egnet familiemateriale til påvisning af sygdomsgen
Udspaltning af et sjældent forekommende recessivt
sygdomsgen sker normalt i forbindelse med indavl
i forholdet 1 til 3. Den statistisk mest optimale situation
er en 1 til 1 udspaltning, men det kan normalt ikke skaffes
ved recessive sygdomsgener, men man kan nøjes med at type
lige så mange raske individer som syge for at få de
mest optimale analyse betingelser.
For at finder frem til
sygdomsgenet skal man regne med typning af ca 10 forældre dyr
der er anlægsbærere og ca 50 stk afkom, hvoraf de 25 har
sygdommen. Man starter med typning af markør 1, derefter
udføres en statistisk analyse. Man fortsætter med typninger af
det næste markørgen indtil man finder koblingen.
Man kan finde den koblede allel ved først DNA-markør,
eller man kan finde den ved markør nr 150,
men man skal i gennemsnit anvende 75 markører før man når frem
til det koblede gen. Den statistisk signifikante
association vil da se således ud:
syg ikke syg
Genotype ------------------------------------
AA | 20 3 | 23
ikke AA | 4 23 | 27
------------------------------------
| 24 26 | 50
DNA-markører anvendt til QTL studier
DNA-markører for quantitative trait loci (QTL) kræver
langt større datamaterialer end for at finde en DNA-markør
for et sygdomsgen, såfremt genet skal påvises i en normalt udavlet
population. QTL'er svarer til de loci, der er omtalt
under definitionen af avlsværdi i lektion 6. De
fremherskende problemer ved påvisning af et QTL er endvidere, at
man ikke ved om der er et der spalter ud i en given
familie. Og man ved heller ikke på nogen måde, hvor stor
effekten i givet fald skal være på en given egenskab.
Der er yderligere det problem, at når man først har
påvist en QTL, kan man ikke på nogen måde være sikker på, at
effekten skyldes et gen, da man ikke umiddelbart kan skelne den fra
to koblede gener med hver sin effekt på den givne egenskab.
Planlægning
af et QTL studier er en sag der skal gøres meget
omhyggeligt, for at man kan forvente at nå frem til
et fornuftigt resultat.
Da man skal type mange dyr for at estimerer en given
QTL tilstrækkeligt præcis til at den kan få praktisk betydning,
og der bør gennemføres statistisk power beregninger for at finde
frem til hvor mange dyr der skal types for at finde en given effekt.
Det er tillige vigtigt at typningerne kan anvendes til at evaluere så
mange egenskaber som muligt. Så når man starter med
at planlægge et QTL studie er det vigtigt at få målt
så mange egenskaber som muligt på de pågældende dyr.
Her kan nævnes alle mulige mål for produktion, mål
for sygdomsforekomst og andre observerbare egenskaber.
Antallet af DNA-markører, der
skal anvendes, svarer dog til de ca. 150, som blev nævnt under
afsnittet om påvisning af DNA-markør for sygdomsgen.
Alternativt til studier af QTL'er i normalpopulationer
kan være at anvende studie af F2 individer
fra specielle eksotiske krydsninger som feks. mellem
tamsvin og vildsvin. Sådanne fundne QTL'er vil imidlertid
ikke umiddelbart kunne anvendes i forbindelse
med det normale avlsarbejde. Sådanne påviste QTL'er
kan imidlertid anvendes i forbindelse med udpegning af kandidatgener,
der kan bidrage til en dybere forståelse af de almindelige
fysiologiske funktioner.
Sire og grandsire design til påvisning af QTL'er
Grand sire designet har været anvendt en hel del indenfor
studie af kvægpopulationer. Det gå ud på at man kun
typer tyrene, idet man udvælger tyre der har et større
antal sønner. Man opdeler da sønnerne i to klasser
dem der har fået et bestemt gen fra faderen og dem der har
fået det andet. Man kan så danne en statistisk kontrast
mellem middel avlsværdien af de to klasser, dem med eller
uden genet fra grand sire. Dette kan gøres for alle
DNA-markører og der er pt. fundet frem til QTL'er for
fedt % og mælkeydelse i amerikanske bestande af Holstein
Frisian, men QTL'erne har endnu ikke været anvendt i praktisk
avlsarbejde.
Fordelen ved grand sire designet er, at der skal types
forholdsvis få individer og man har en 1 til 1 udspaltning blandt
afkommet, men en af begrænsningerne er,
at der kun kan estimeres additive effekter, hvilket er
tilfældet i sire designet.
Sire designet; her types alle individer der måles såvel
som forældre dyrene. Men da DNA-markørerne er mest interessante
for egenskaber med lav heritabilitet skal der types mange
dyr for at få et rimeligt præcist skøn for effekterne. Man
får her alle tre genotype klasser blandt afkom med 1:2:1 udspaltning.
Variansen på en geneffekt (middelværdi) er omvendt
proportional med antallet, på hvilket geneffekten
er baseret.
En kontrast mellem to effekter kan i princippet
evalueres med
et t-test, her er det også den middelværdi der er baseret
på færrest antal der bestemmer hvor stærk testet er.
Forskellene er påvist i en population med middel sygdomsfrekvens på 10 %. Syg ikke
syg er binominalfordelt med variansen 0,1*0,9/N hvor antallet er testede dyr
i en klasse. S.D. er beregnet som sqrt(0,1*0,9/N + 0,1*0,9/N) og t = dif/S.D. og anvendelse
af 5% signifikansgrænser.
| Antal A1 | Antal A2 | S.D. | Mindste signifikante differens i sygdomsfrekvens |
| 5000 | 5000 | 0,00600 | 1,8 % enheder |
| 500 | 500 | 0,0190 | 5,7 % enheder |
| 100 | 100 | 0,0420 | 12,6 % enheder |
Figur 12.2. Viser de to klassiske design sire og grand sire til påvisning af QTL'er med test af afkom for markørgen og fænotype måling. Contrasterne kan sammenlignes med t-test.
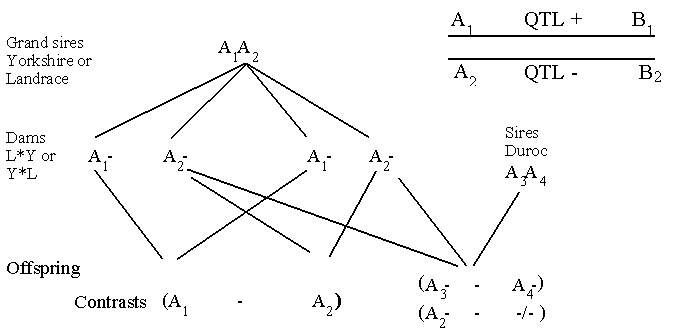 |
Der findes i litteraturen talrige beretninger om vellykket selektion mod arveligt betingede sygdomme; men i næsten alle tilfælde drejer det sig om simpelt recessive egenskaber, som bekæmpes ret rutinemæssigt. Dog er der naturligvis problemer i de tilfælde, hvor den iværksatte selektion modvirkes således som man kommer ud for i forbindelse med overdominansfænomenet, hvor heterozygoterne har en større reproduktionsegnethed (fitness) end homozygoterne.
Når der derimod er tale om sygdomme med en polygenisk disposition, er beretninger om heldigt udført selektion sparsomme for de større husdyrs vedkommende. De resultater, der er opnået i retning af større sygdomsresistens, er for en stor del baseret på krydsning. At det ikke blot i teorien, men også i praksis er muligt at opnå væsentlige resultater af selektion mod specifikke sygdomme, er med stor tydelighed vist indenfor hønseavlen og ved avl med laboratoriedyr.
| Figur 12.3. Selektions forsøg for og imod neoplasma dødsfald hos høns. |
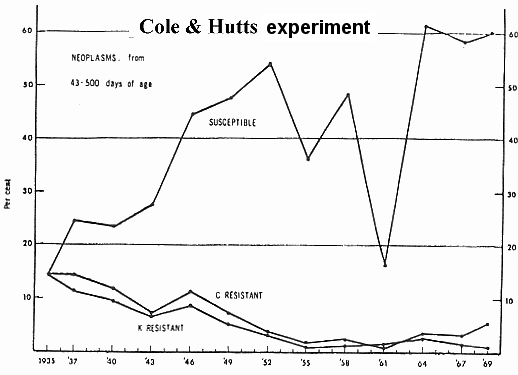 |
Initialgenerationen var uselekteret, men for hver af de følgende generationer udvalgtes resistente avlsdyr i hver linje. I 1935 etableredes tillige en tredje linje, S, på grundlag af individer, der var modtagelige (susceptible line) for leukose. Denne linje blev i alle følgende generationer vedligeholdt ved fortsat selektion af avlsdyr, der var modtagelige. De tre linjer opholdt sig i fælles miljø. Bortset fra perioden 1958-61 (jf. grafen) må miljøet antages at have været virusinficeret i betydelig grad i hele forsøgsperioden. Figuren viser tydeligt, at selektionen har været ret effektiv i begge retninger, idet der ved forsøgets afslutning (opgørelse 1967-69) var en neoplasme -dødelighed på ca. 60 % i den modtagelige linje, medens de to resistente linjer, C og K, havde en neoplasme-dødelighed på henholdsvis 3,7 % og 0,9 %. I samme periode reduceredes det totale antal dødsfald fra 51,5 % (C) og 44,4 % (K) til henholdsvis 12,7 % og 8,0 %. Dødsfaldene er opgjort i perioden fra 43 til 500 dage efter klækningen. De nævnte selektionsresultater er opnået til trods for forholdsvise lave heritabilitetsestimater og til trods for, at der samtidig blev selekteret for mange andre egenskaber. De gode resultater må dog forklares med, at der er anvendt afkomsundersøgelser som udvalgskriterium. I øvrigt mener Cole & Hutt, at samme resultater kunne være opnået på betydeligt kortere tid under anvendelse af en selektionsprocedure, som kun blev anvendt i en del af forsøgsperioden.
Da leukocyter er af betydning ved udvikling af resistens, er det af interesse at vide, at det er muligt at selektere for højt og lavt leukocyttal i blodet (WBC= white blood cell). Sådanne forsøg er udført hos mus (Chai 1975, J.Heredity 66:301-309). I initial populationen, (generation 0) havde man et leukocyttal på 6-8 x 103 pr. mm3. Efter 22 generationers selektion i HLC (high leucocyte count) og LLC (low leucocyte count) linjerne nået tallene henholdsvis 36-38 x 103 og 4-5 x 103, medens kontrolpopulationen har nået et niveau på ca . 10 x 103 , altså ikke væsentligt forskelligt fra initialpopulationens (en evt. signifikant forskel kan bero på "random genetic drift").
I relation til dette selektionsforsøg skal til sidst nævnes, at man har beregnet en h2 værdi på 0,20 for lymfocyttallet hos visse kvægracer. Hvis det er ønskeligt, kan lymfocyttallet altså let ændres ved selektion.
| Figur 12.4. Selektions forsøg for højt og for lavt antistof titer mod fåre erotrocytter hos mus. |
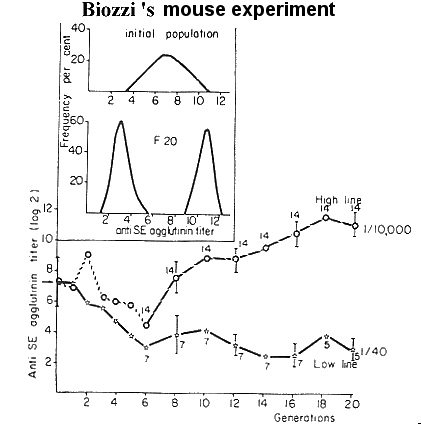 |
For at afprøve de af Biozzi et al. (1972, J.Exp.Med. 135:1071-1094) selekteret mus for højt og lavt antistofrespons i forbindelse med experimentel immunisering, er der gennemført en lang række challenge forsøg med experimentelle infektioner på de to muselinier. Det skal her bemærkes at de mus der har et højt generelt antistofsvar generelt har et dårligt cellulært forsvar. Individer med godt cellulært forsvar vil fjerne antigenerne v.h.a. deres makrofager, og derfor vil antigenet blive fjernet, før der kan dannes antistof mod det. Så det naturen har fundet frem til er et kompromis mellem et godt cellulært og humoralt immunforsvar, som det også fremgår af figur 12.5.
| Figur 12.5. Challenge forsøg med forskellige mikroorganismer på dyr selekteret for højt og for lavt antistof titter mod fåre erotrocytter hos mus. |
 |
Konklusion:
Den konklusion som kan drages fra de gamle forsøg må være, at det er muligt at avle for speciel
resistens, men en sådan avl vil normalt blive overhalet af muligheden for vaccination, hvilket
også er sket for hønseleukose vedkommende. Det må endvidere konkluderes, at det ikke er
muligt at selektere for generel resistens ved at selektere for høje eller lave værdier af
immunitetens komponenter, idet de er modsat rettede og deres naturlige niveau vil være
balanceret i forhold til en populations historie med hensyn til infektiøse agens. Så renavl kan
ikke benyttes til at forbedre den generelle resistens
baseret på de immunologiske komponenter. Men hvad med krydsning?
Ved at se på Biozzi's graf fra callenge forsøget kan man konkludere,
at det alt andet lige er bedst at ligge i
nærheden af middelværdien, idet det er de ekstreme dyr,
der udsættes for de sværeste sygdomsangreb. Så et af midlerne til at opnå så
lav sygelighed som muligt er at
arbejde med en ensartet population af dyr med den optimale middelværdi.
Ensartethed kan opnås via krydsningsdyr. Tovejs, trevejs eller
tilbagekrydsninger er på grund af dominansforholdene mere ensartede end renavlsdyr.
Det skulle derfor være muligt at finde frem til krydsningskombinationer, der
har den rigtige middelværdi i
forhold til en populationens sygdomsudfordringer.
F2 dyr eller fire-vejskrydsninger er mere
heterogene, og ydergrupperne vil derfor, som i renavlspopulationer,
være mere udsatte for forskellige sygdomme, så
anvendelse af den type dyr i produktionen bør normalt undgås.
Der foreligger p.t. ingen praktiske forsøg, der kan verificere de fremsatte postulater
vedr. forskel i sygelighed mellem de forskellige krydsningstyper. Der bør derfor snarest
iværksættes analyser af disse forhold.
Opgaver, Lektion 2, link løsninger
1 Betragt kvægets Zz blodtypesystem med de tre blodtyper Z, Zz og z. I nedenstående tabel er angivet blodtypefordelingen i tre stikprøver fra racerne RDM, SDM og Jersey. Hvordan forventes blodtypefordelingen at blive i den følgende generation efter tilfældig parring inden for racerne? Race Blodtypefordeling (antal) Z Zz z RDM 28 340 1.032 SDM 2 55 318 Jersey 56 129 75 2 Betragt en stor tilfældigt sammenparret population. På et locus med to alleler A og a, hvor A dominerer over a, er frekvensen af homozy- gotisk recessive individer (aa) 1%. a) Hvad er frekvensen af heterozygotiske individer (Aa)? b) Hvilken del udgør disse (Aa) af individer med den dominante fænotype? 3 I en population med tilfældig parring forekommer et recessivt sygdomsgen (a) med frekvensen 0,005. a) Angiv sandsynligheden for i populationen at finde raske forældre (A-) med afficeret afkom (aa). b) Angiv sandsynligheden for i populationen at finde forældre, hvoraf mindst én er syg (aa) med afficeret afkom (aa). c) Angiv det talmæssige forhold mellem de under punkt a) og punkt b) fundne sandsynligheder og kommentér det fundne resultat. 4 Hos gravhunde findes et par allele gener R og r, der er bestemmende for hårtypen med R dominerende over r. Fænotyperne er henholdsvis ruhåret (R-) og korthåret (rr). a) Blandt 100 gravhunde i H.W.-ligevægt er påvist 64 ruhårede og 36 korthårede. Hvor mange gravhunde må antages at være bærere af et skjult anlæg for korthårethed i denne population? b) I en anden bestand af gravhunde er det klarlagt, at forholdet mellem genotyperne RR og Rr er som 2:5. Hvor stor er sandsynligheden for, at den første hvalp bliver korthåret efter sammenparring af to tilfældigt valgte ruhårede hunde? 5 I en population fandt man, at én af 10.000 mænd led af hæmophili, mens der ikke fandtes angrebne kvinder. (Hæmophili er en kønsbunden recessiv egenskab). a) Hvad er frekvensen af genet for hæmophili (h) blandt mænd? b) Hvad er sandsynligheden for, at der fødes kvinder med hæmophili, når det antages, at genfrekvensen er den samme hos mænd og kvinder? 6 Et forældrepar, hvor moderen har blodtype B og faderen blodtype A, har et barn med blodtype 0. Hvilken blodtyper kan deres eventuelle fremtidige børn få? 7 Fra en russisk rævepopulation blev indfanget 14.345 ræve. Af disse var 12 sorte, 678 intermediære og 13.655 røde. a) Beregn frekvensen af genet for henholdsvis rød og sort farve. b) Undersøg ved en Chi-i-anden test, om de observerede antal stemmer overens med de forventede under H-W ligevægt. 8 I det følgende forudsættes, at der i den danske Schæferhundepopulation er tilfældig parring. Mikrosatellit locus A er autosomalt og har 3 alleler A1, A2 og A3 med frekvenserne henholdsvis 0,1, 0,3 og 0,6. Mikrosatellit locus B er ligeledes autosomalt. Dette locus har 3 alleler B1, B2 og B3 med frekvenserne henholdsvis 0,2, 0,3 og 0,5. a) Angiv de forventede genotyper og de forventede genotypefrekvenser i populationen for hvert locus. b) Angiv den forventede frekvens af genotypen A1A2B1B2 og af genotypen A3A3B3B3 i populationen. En hanhund med genotypen A1A2B1B2 parres med et antal tæver med genotypen A3A3B3B3. c) Angiv de forventede genotyper blandt afkom efter nævnte parringer og angiv den forventede fordeling (udspaltning) af disse genotyper blandt afkommet under antagelse af, at de to loci ikke er genetisk koblede. d) Angiv de forventede genotyper blandt afkom efter nævnte parringer og angiv den forventede procentvise fordeling af disse genotyper blandt afkommet under antagelse af, at de to loci er koblede med en overkrydsningsfrekvens på 0,20, og at hanhunden bærer generne A1 og B1 på samme kromosom, dvs. A1 og B1 er i koblingsfase. 9 På grisens kromosom 6 er der to tæt-koblede sygdomsgener. Det ene gen, Calcium Release Channel (CRC), er ansvarligt for den recessive lidelse Porcine Stress Syndrome (Stressfølsomhed). Grise med genotypen n/n er stressfølsomme, mens grise med genotyperne N/n og N/N er normale. Det andet gen, 1,2 alfafucosyltransferase 1 (FUT1), er ansvarligt for, om grisene bliver modtagelige for ødemsyge. Modtagelighed for ødemsyge nedarves dominant, således at grise med genotyperne E/E og E/e er modtagelige, mens grise med genotypen e/e er modstandsdygtige overfor ødemsyge. a) Hos en sjælden griserace er CRC allelen N og FUT1 allelen E altid i koblingsfase. Frekvensen af N allelen er 0,4, og frekvensen af E allelen er 0,3. Angiv haplotyperne samt deres frekvenser. b) En avler af den sjældne race fjerner alle stressfølsomme grise (nn) i en generation. Hvilken betydning vil dette have for grisenes modtagelighed over for ødemsyge? Beregn haplotypefrekvenserne efter selektion. c) Den genetiske afstand mellem CRC og FUT1 er 5 map units. Der findes DNA tests, så både CRC og FUT1 genotyperne kan fastlægges. Hvorledes kan disse DNA tests bruges til generelt at fremavle grise, som er både stressfrie og modstandsdygtige overfor ødemsyge? 10 To loci A og B er genetisk koblede med en rekombinationsfrekvens på 0,3. I en population med tilfældig sammenparring findes følgende gamet- frekvenser. Gamet AB Ab aB ab ___________________________________________ Frekvens 0,4 0,1 0,2 0,3 a) Beregn koblingsuligevægten D. b) Beregn D i de følgende 10 generationer. c) Beregn gametfrekvensen ved koblingsligevægt, d.v.s. mår D er 0. d) Beregn hyppigheden af dobbelt heterozygoter i udgangs- populationen og ved koblingsligevægt.
Opgaver, Lektion 3, link løsninger
1 I en population blev fundet nedenstående genotypefordeling: AA Aa aa 110 225 115 a) Er populationen i Hardy-Weinberg ligevægt? b) Der sker herefter en selektion mod aa med selektionskoef- ficienten s = 0,1. Beregn genfrekvenserne i næste fem generationer. 2 Inden for SDM findes en uønsket farvemutant, således at individer med genotypen ee er rødbrogede, mens de sortbrogede har genotypen E-. Inden for en tilfældigt parrende bestand af sortbroget kvæg, hvor gen- frekvensen for E er p, elimineres rødbroget kvæg fuldstændigt fra hver ny afkomsgeneration. a) Hvor mange generationer vil det tage at halvere frekvensen af rødbrogede kalve, hvis frekvensen af p0 = 0,80? b) Samme spørgsmål som a) med p0 = 0,98. c) Kommenter det talmæssige forhold mellem svarene i b) og c). 3 I et autosomalt, toallelt system med overdominans er der følgende sammenhæng mellem genotyper og fitness: Genotyper A1A1 A1A2 A2A2 Fitness 0,8 1 0,3 a) Beregn genfrekvenserne ved genfrekvensligevægt. b) Beregn herefter genotypefrekvenserne forud for selektion, c) og beregn genotypefrekvenserne efter selektion. 4 I en population er frekvensen af seglcelleanæmi fundet at være 0,05 blandt nyfødte. På grund af resistens mod malaria får heterozygoterne mest afkom, således at de normale individer (Hba/Hba) og de anæmiske individer (Hbs/Hbs) kun bidrager med henholdsvis 80% og 10% afkom i forhold til afkom fra heterozygoter (Hba/Hbs). a) Hvad vil frekvensen af Hbs være, når populationen er i ligevægt? b) Vil antallet af nyfødte med seglcelleanæmi vokse eller falde? 5 I en dansk undersøgelse af 94.000 fødsler fandtes 10 tilfælde af chondrodystrofe dværge (dominant betinget misdannelse). Det antages, at de observerede dværge er heterozygoter. a) Hvad er genfrekvensen af sygdomsgenet? b) Find fertiliteten (som i dette tilfælde er lig med fitness) af dværgene (Cc) relativt til normale (cc), når det fra en anden dansk undersøgelse vides, at 108 voksne dværge havde fået 27 børn, mens 457 normale søskende havde fået 582 børn. c) Det antages, at den danske population er i mutation-selektions ligevægt med hensyn til denne sygdom. Giv ud fra resultaterne i a) og b) et skøn for mutationsfrekvensen c til C. 6 En lukket population omfatter i hver generation 20 avlshanner og 20 avlshunner. I generation 0 er genfrekvenserne på et givet locus følgende: p = 0,6 og q = 0,4 Generation 1 dannes ved tilfældig parring. Angiv mulige udfald af genfrekvenser i generation 1, idet der benyttes sikkerhedsgrænser svarende til en sandsynlighed på p = 5% i en normal fordeling. 7 En lukket population er sammensat af fem avlshanner og 50 avlshunner generation efter generation. Man ønsker at sammensætte en anden lukket population bestående af avlshanner og avlshunner i forholdet 1:1. a) Hvor mange individer skal sidstnævnte population omfatte, hvis den effektive populationsstørrelse skal være uændret? b) Hvor stor er ændringen i indavlsgraden pr. generation i de to populationer?
Opgaver, Lektion 4, link løsninger
1 Hvad er indavlskoefficienten for individet X i nedenstående diagram?2 Beregn indavlskoefficienten for samtlige individer i følgende diagram: Dyr Far Mor Idet A=1 B=2 C=3 D=4 E=5 0=ukendt 1 0 0 2 1 0 3 1 2 4 3 2 5 3 4 3 På grundlag af nedenstående stamtavle ønskes følgende spørgsmål besvaret: a) Opstil et pilediagram for individet A. b) Beregn indavlsgraden for alle indavlede individer. 4 Betragt følgende to stamtavler. a) Hvem er fælles ane for Wahl 239 og ko nr. 196? b) Hvor stor bliver indavlskoefficienten på en kalv efter Wahl 239 og ko nr. 196? c) Kan det anbefales at bruge tyren Wahl 239 ved insemination af ko nr. 196? 5 På basis af nedenstående stamtavler for mink ønskes følgende spørgsmål besvaret: a) Angiv hvilke dyr, der er indavlede. b) Opstil pilediagram og beregn indavlskoefficienten for afkom efter IV A og IV B. 6 I nedenanførte stamtavle er de oprindelige betegnelser for de enkelte individer erstattet med numrene 1 til 11. Beregn indavlskoefficienten for dyr nr. 10 og 11, og beregn det additive slægtskab mellem dyr nr. 11 og de øvrige dyr i stamtavlen. 7 I nedenanførte genealogiske diagram repræsenterer V 12 (probant) den først erkendte schæfer-dværg i Danmark. Denne dværgvækst nedarves som en autosomal, recessiv egenskab. a) Angiv de individer, der med sikkerhed må være heterozygotiske anlægsbærere. b) Hvor stor er sandsynligheden for, at en tilfældigt udtaget phenotypisk normal hvalp i et af de to kuld (A eller B) i generation V er heterozygotisk anlægsbærer for dværgvækst? c) Hvor stor er indavlsgraden for 1) en tilfældigt udtaget hvalp i kuld A, og for 2) en tilfældigt udtaget hvalp i kuld B? d) Hvor stor er slægtskabskoefficienten mellem to tilfældigt udtagne hvalpe i kuld A? 8 På en minkfarm er der 100 avlsdyr, af hvilke 60 er ubeslægtede, otte er afkom efter helsøskendeavl, og 32 er afkom efter halvsøskendeavl. Beregn den gennemsnitlige indavlsgrad for de 100 avlsdyr.
Opgaver, Lektion 5, link løsninger
1 Nedenfor er angivet en stamtavle, der viser den autosomale defekt ataksi (aa) hos hunde i et kuld efter normale (A-), men beslægtede forældre III 4 og III 8. Da denne defekt er sjælden, kan det antages, at II 1 og II 6 ikke bærer genet a.a) Giv en liste over de hunde, hvor genotypen kan fastlægges og angiv typen. b) Hvor stor er sandsynligheden for, at det klinisk sunde dyr IV 2 er anlægsbærer? 2 På en klinik for mindre husdyr har man påvist en sjælden enzymdefekt hos en hanhund IV 1. På grundlag af ejerens oplysninger og laboratorie- mæssig undersøgelse af alle nulevende søskende og aner kunne nedenanførte genealogiske diagram konstrueres. Hvilken monofaktoriel arvegang må anses for at være den mest sandsynlige på enzymdefektens forekomst? Mulighederne skal behandles hver for sig. 3 Hos menneske og kanin er der fundet en anomali, som manifesterer sig blandt andet i leukocyternes form. I nedenstående stamtavle er vist forekomsten af "syge" og normale individer. Giv en udførlig motivering for hvilken arvegang, der er mest sandsynlig, og hvilke der sandsynligvis kan udelukkes (monofaktoriel nedarvning antages). 4 Pelsdyravlere har påvist en ny pelskvalitet hos en han, I 1 og har yderligere opnået de resultater, der er anført i det genealogiske diagram. Udfyldt symbol betegner ny pelskvalitet. a) Under antagelse af monofaktoriel nedarvning ønskes en redegørelse for den nyopdukkede egenskabs arvegang. b) Beskriv en avlsmetode, der kan anvendes til verificering af arvegangen. 5 Hos hvilket køn vil man forvente, at en recessiv kønsbunden mutant- egenskab viser sig. a) Hos høns? b) Hos kaniner? 6 En tyr, der er importeret fra Canada, er mistænkt for at være anlægsbærer af en uønsket recessiv egenskab, som er meget sjælden inden for den pågældende race her i landet. a) Skitsér en metode til afprøvning af tyren for det pågældende anlæg. b) Beregn det antal individer, der er nødvendige i undersøgelsen for at kunne udtale sig med 95% sikkerhed. c) Giv en klar formulering af det mulige resultat af undersøgelsen. 7 Man ønsker gennem afkomsprøve at fastlægge, om en tyr er anlægsbærer for et bestemt recessivt gen. Dette kan ske ved at parre tyren med a) Køer af den recessive type (aa) b) Køer, som man ved er heterozygote (Aa) c) Egne døtre Hvis alt afkommet er normalt, hvor mange stk. afkom må tyren give i disse tre forskellige tests, for at sandsynligheden for at den ikke er anlægsbærer er 95%? 8 I det genealogiske diagram repræsenterer I 1 og I 2 en tilfældigt udtaget orne og en tilfældigt udtaget so inden for Dansk Landrace midt i 1980erne, hvor frekvensen af det recessive halotangen n var høj, idet der fødtes 4% halotan-følsomme grise (genotype nn). Samtlige grise i diagrammet blev halotantestet i 6-7 ugers alderen. Testen viste, at III 2 og III 4 var halotanfølsomme. I populationerne som helhed var der tilfældig parring. a) Angiv de individer, der med sikkerhed må være anlægsbærere for halotangenet n, og angiv sandsynligheden for, at henholdsvis III 1, III 3 og III 5 er anlægsbærere. b) Hvad er sandsynligheden for, at I 2 er anlægsbærer, idet resultatet angives på basis af det faktum, at der fødes 4% halotanfølsomme i populationen. c) Idet det antages, at II 2 er anlægsbærer, hvad er da sandsynlig- heden for, at III 6 er genotypisk normal (dvs. genotype Hal NN)? 9 Blandt 120 stk. afkom efter heterozygotiske forældre (parringstype: Aa x Aa) er følgende udspaltningsforhold påvist: Genotype Antal AA 39 Aa 51 aa 30 Undersøg ved hjælp af Chi-i-anden test, om der er statistisk signifikant afvigelse fra den forventede udspaltning. 10 Der foretages en tilbagekrydsning, det vil sige homozygot x heterozygot, for at teste om en karakter nedarves recessivt. Der er i alt 30 tilbage- krydsningsindivider. Undersøg ved hjælp af Chi-i-anden-test for hvilke talforhold hypotesen om recessiv nedarvning kan accepteres (1:1 spaltning), når 5% signifikansgrænsen anvendes. 11 Angiv sandsynligheden for en kønsfordeling på to hanner og fire hunner i et kuld minkhvalpe på seks stk. Kønskvotienten sættes til 50%. 12 Hos kvæg dominerer kullet (uden horn) P- over hornet pp. Hvor stor er sandsynligheden for, at en heterozygotisk ko får én kullet + tre hornede kalve efter inseminering med heterozygotiske tyre? 13 Angiv mulige kombinationer af AA, Aa og aa i familier på tre søskende efter parring mellem heterozygotiske forældre. 14 Afkom efter en fænotypisk normal orne og fire fænotypisk normale søer, som alle fem var kendte bærere af anlæg for krogede baglemmer, viste følgende udspaltningsforhold: Foto, Lars Wichmann Madsen viser nyere billede med tilsvarende symptomer. Normale Afficerede ------------------------------- So nr. 1 6 3 So nr. 2 10 2 So nr. 3 12 3 So nr. 4 5 0 ------------------------------- Undersøg med statistisk test om disse udspaltningsforhold er i overens- stemmelse med en hypotese om recessiv nedarvning. 15 Undersøg om udspaltningen af recessive i nedenstående familiemateriale hos kvæg er i overensstemmelse med en 7:1 spaltning, idet både faderen og morfaderen antages at være anlægsbærere. Familierne er fundet på grundlag af mindst et afficeret afkom. Familie-størrelse Antal afficerede --------------------------------------- 2 1 2 1 2 1 2 1 2 1 3 1 5 1 6 1 6 1 8 2 15 2 ---------------------------------------- 16 Hos grise er der påvist en form for lamhed af forbenene, som forekommer sporadisk i kuld efter normale forældre. I en større besætning blev anomalien påvist hos grise i seks kuld, og fordelingen var følgende: Kuld nr. Normale Afficerede* ----------------------------------- 1 5 3 2 4 3 3 4 1 4 7 3 5 7 3 6 9 2 ----------------------------------- * Ligeligt fordelt mellem orne- og sogrise. Angiv den genetiske hypotese, der svarer bedst til de indsamlede data. Der ønskes en statistisk afprøvning af denne hypotese.
Opgaver, Lektion 6, link løsninger
1 I en hønsebestand er der tre genotyper svarende til generne Rd og rd på riboflavin-locus. Det gennemsnitlige indhold af riboflavin i mikrogram pr. gram æggeblomme er 4,30 for Rd/Rd høner og 0,40 for rd/rd høner, mens det er 2,50 for heterozygotiske høner. Frekvensen af Rd og rd er henholdsvis 0,7 og 0,3. Hvor stort er det gennemsnitlige riboflavinindhold pr. gram blomme under forudsætning af, at alle høner i bestanden lægger lige mange æg, og at blommevægten er ens for alle æg? 2 Hos SDM malkekvæg er der fundet et QTL med effekt på hyppigheden af tvillingefødsler. Den QTL allel, der har en positiv indflydelse på tvillingefødsler har en allel frekvens på 0,2. Der blev fundet følgende effekter: Genotype aa Aa AA Frekvens af tvillinger 0,008 0,016 0,020 a) Beregn populationensfrkvensen af tvillinger. b) Beregn de tre genotypiske værdiers afvigelser fra populations- gennemsnittet. c) Opdel genotypeværdiernes afvigelse fra populationsgennemsnittet i en additiv del (avlsværdi) og en dominansafvigelse. 3 I en svinebesætning er svinenes vægt ved fem måneder i gennemsnit 88,5 kg. De i avlen anvendte gylte vejer i gennemsnit 93,0 kg, og de anvendte orner vejer 102,0 kg ved fem måneder. Afkommet vejer i gennemsnit ved fem måneder 89,5 kg. Beregn heritabiliteten for vægt ved fem måneder. 4 En tyr anvendtes til to grupper køer, hvis gennemsnitlige ydelse af smørfedt (smf.) var: Gruppe I: 295 kg smf. Gruppe II: 227 kg smf. Afkommet efter de to grupper ydede henholdsvis 266 og 259 kg smf. Beregn h2 for smf. 5 Tegn et pilediagram over relationen henholdsvis mellem halvsøskende og mellem helsøskende. Anfør den forventede fænotypiske korrelation henholdsvis mellem halvsøskende og mellem helsøskende. Korrelationen udtrykkes ved det additive slægtskab (a) og ved h2 og c2. 6 På grundlag af et større observationssæt er der beregnet korrelation mellem beslægtede individer for vægt ved 6 uger hos grise. Resultaterne var følgende: Mellem halvsøskende 0,05 Mellem helsøskende 0,25 Beregn heritabiliteten i de to tilfælde, idet der refereres til formel for forventet korrelation mellem beslægtede individer. Er der en fælles miljø komponent for helsøskende, og i givet fald hvorfor? 7 På grundlag af et observationssæt er der beregnet korrelation og regression mellem beslægtede individer for højde hos veterinær- studerende og deres forældre i 1998. Resultaterne var følgende: Korrelationen mor-afkom 0,45 far-afkom 0,20 Regression afkom-gns. forældre 0,65 Beregn h2 i de tre tilfælde og diskuter årsager til forskellene mellem resultaterne:
Opgaver, Lektion 7, link løsninger
1 Når man skal vælge mellem alternative metoder til at vurdere et dyrs avlsværdi, er det væsentligt at kende avlsværdiestimatets sikkerhed. Antag at en egenskab med heritabiliteten h2 = 0,25 kan vurderes på grundlag af:1) moderens præstation 2) 50 halvsøskendes præstation 3) 20 stk. afkom, der indbyrdes er halvsøskende (Jvf. figur, hvor dyret, hvis avlsværdi skal bestemmes, er markeret med sort). Hvilken af de tre metoder giver den største sikkerhed? 2 Beregn avlsværdiestimat for mælkeydelse for følgende dyr (h2 = 0,25, c2 = 0,05 og populationsgennemsnit = 4500 kg), idet avlsværdiestimatet baseres på kendskab til egen ydelse eller ydelse af beslægtede individer. 1) egen ydelse 1. laktation 5000 kg mælk 2) gns. af egen ydelse i tre laktationer 4700 kg mælk 3) gns. af moderens ydelse i tre laktationer 5000 kg mælk 4) gns. af 100 paternelle halvsøskende 4600 kg mælk 5) afkom efter 3) og 4) Hvilket af avlsværdiestimaterne er beregnet med størst sikkerhed? 3 Hos svenske sportsheste forekommer syndromet osteochondrose (OCD) med en hyppighed på 30% (dvs. 30% OCD, 70% OCD-fri). Populationen kan betragtes som et resultat af tilfældig parring. Den genetiske disposition er polygenisk og har en heritabilitet på 0,20. Den relative værdi af individer med OCD sættes til 0, medens værdien af OCD-fri individer er 1. A har 40 stk. afkom, af hvilke 20 er OCD-fri og 20 har OCD. B har 60 stk. afkom, af hvilke 45 er OCD-fri og 15 har OCD. C har 20 stk. afkom, af hvilke 16 er OCD-fri og 4 har OCD. a) Beregn populationsgennemsnittet og beregn gennemsnittet for de 3 afkomsgrupper. b) Beregn de tre hingstes (A, B og C's) avlsværdiestimat, idet alle individer inden for hver afkomsgruppe er paternelle halvsøskende. 4 Beregn sikkerheden kvadreret på avlsværdiestimaterne for 5 individer som har følgende observationssæt: 1) egen ydelse 2) gns. af 5 egen præstationer 3) gns. af 200 paternelle halvsøskende 4) gns. af 10 stk. afkom, der indbyrdes er halvsøskende 5) gns. af 200 stk. afkom, der indbyrdes er halvsøskende idet h2 = 0,05, 0,1, 0,2, 0,4 og 0,6 og c2 = 0,10. Kommenter resultaterne. 5 Udled formel for avlsværdi indeks og sikkerheden kvadreret for 4 individer med information fra: 1) egen præstation 2) de to forældres præstationer 3) de fire bedsteforældres præstationer 4) de otte oldeforældres præstationer Kommenter resultaterne.
Opgaver, Lektion 8, link løsninger
1 Heritabiliteten for tilvækst (20-90 kg) hos svin sættes til 0,30. I en besætning er den gennemsnitlige tilvækst 935 g. De i avlen benyttede gylte havde en gennemsnitlig tilvækst på 970 g, og de anvendte orner en tilvækst på 1008 g. Hvor stor gennemsnitlig tilvækst forventes for afkommet efter de selekterede individer? 2 I en minkbestand bruges 5% hanner og 33% hunner til avl. Der selekteres for kropsstørrelse, som har sigmaP på 0,3 og 0,2 kg. for henholdsvis hanner og hunner. Heritabiliteten for kropsstørrelse er 0,40. Hvor stor genetisk ændring forventer man pr. generation? 3 Det antages, at en population af høner har en årlig gennemsnitsydelse på 230 æg. Den fænotypiske standardafvigelse er 35,7 æg. Der regnes endvidere med en heritabilitet på 0,40 for årlig ægydelse. Selektionen baseres udelukkende på høner, og 20 procent af de højestydende høner benyttes til avl. Beregn følgende: a) Selektionsdifferencen (antal æg). b) Den genetiske ændring (antal æg) fra moder- til dattergenerationen. c) Døtrenes gennemsnitlige ægydelse pr. år. 4 Hoftedysplasi hos hunde er en tærskelegenskab med en heritabilitet på 0,3. Ca. 30% af alle Schæferhunde har hoftedysplasi. De 70%, der er phenotypisk raske, sættes til samme avlsværdi, hvis man udelukkende baserer avlsværdien på grundlag af en simpel fortolkning (enten eller) af røntgenbillederne af de enkelte hunde. a) Antag, at der blandt de 70% raske Schæferhunde udtages en til- fældig stikprøve som avlsdyr. Hvor stor er selektionsintensi- teten? b) Angiv den forventede genetiske ændring i fænotypiske standard- enheder pr. generation, hvis man anvender de 70% raske Schæfer- hunde som avlsdyr. c) Beregn delta G i sigmaP-enheder, hvis tæverne udvælges ved individprøve, mens hannerne udvælges på grundlag af afkoms- undersøgelse (20 stk. halvsøskende-afkom), idet der anvendes 10% til avl. d) Beregn forholdet mellem delta G beregnet under punkt c) og b). 5 Der planlægges en afkomsprøvestation for mink for at forbedre en pelsegenskab, der har en heritabilitet på 0,2. Stationen skal have en kapacitet på 800 stk. afkom pr. generation, det vil sige højst 800 fædre kan blive afprøvet. Selektionen ønskes foretaget sådan, at 40 af de undersøgte fædre udvælges til avl. Der indsættes udelukkende paternelle halvsøskendegrupper på stationen, og af det foregående fremgår, at antallet af afkom pr. fader kan variere mellem 1 og 20. Hvor mange stk. afkom pr. fader skal man afprøve for at den genetiske ændring pr. generation er størst mulig? 6 To allele gener har begge en frekvens på 0,5. Genparret giver anledning til variation i en kvantitativ egenskab, således at der er en forskel på 4 kg i den kvantitative egenskab mellem de to typer af homozygoter. Der er fuldstændig dominans på det pågældende locus. Den kvantitative egenskab har sigmaA = 10 kg og sigmaP = 20 kg. a) Hvor stor en del af den kvantitative egenskabs additive varians skyldes pågældende locus? b) Giv kommentarer til hvornår det er formålstjenligt anvende genmarkører. 7 I et selektionseksperiment med mus, som løb over ni generationer, blev der ved individuel selektion selekteret for tilvækst (x), og der blev i de ni generationer målt en genetisk ændring på 2,34 g. Som korreleret effekt blev der målt en ændring i kuldstørrelse (y) på 0,693 unge pr. kuld over de samme ni generationer. Egenskab heritabilitet variansP x 0,23 5,59 y 0,15 5,18 a) Beregn den genetiske korrelation mellem tilvækst og kuldstør- relse. b) Beregn selektionsintensiteten ix.
Opgaver, Lektion 9, link løsninger
1 I en marsvinebestand, hvor der opretholdes en indavlskoefficient på F = 0,25, er der tre vægtklasser: 100 g, 80 g og 50 g, svarende til genotyperne A1A1, A1A2 og A2A2. Frekvensen af A1 og A2 er henholdsvis 0,8 og 0,2. a) Hvor stor er den gennemsnitlige vægt? b) Beregn indavlsdepressionen. 2 I et krydsningsforsøg med svin er der fundet følgende gennemsnitlige vægttal i kg ved 80 dages alder: Linie Krydsning A B F1 (A x B) Ikke indavlede 22,7 20,1 22,8 Indavlede 21,7 13,1 19,6 a) Beregn graden af heterosis ved krydsninger mellem 1) ikke- indavlede linier og 2) indavlede linier. Resultaterne angives såvel i absolutte som relative tal. b) Beregn indavlsdepressionen udtrykt i procent.
Løsninger, Lektion 2, link opgaver
1 Genfrekvensen for Z og z i blodtypesystemet bliver efter gentælle metoden. Race Genfrekvens p(Z) q(z) RDM 0,14 0,86 SDM 0,08 0,92 Jersey 0,46 0,54 De forventede H-W ligevægts genotypefrekvenser hos afkom. Race p2 2pq q2 Z Zz z RDM 0,02 0,24 0,74 SDM 0,01 0,15 0,84 Jersey 0,21 0,50 0,29 2 I en tilfældig sammenparret population svarer frekvensen af homozygotisk recessive individer (aa) til q2 = 0,01, hvilket giver q=0,1 og p=0,9. a) Frekvensen af heterozygotiske individer (Aa) = 2pq = 0,18. b) De dominante fænotyper består af AA og Aa, hvoraf Aa individer udgør 2pq/(p2 + 2pq) = 0,182 3 Genfrekvensen af sygdomsgenet er 0,005. a) Sandsynligheden for i populationen at finde raske forældre (A-) med afficeret afkom er (2pq)2*(1/4) = 2*10-5 b) Sandsynligheden for i populationen at finde forældre, hvoraf mindst én er syg med afficeret afkom 1) den ene forælder syg 2*(2pq)*q2*(1/2). 2) begge forældre syge q2*q2 =q4. sum 2*10-7 c) Forhold mellem de under punkt a) og punkt b) fundne sandsynlig- heder (2pq)2*(1/4)/[2*(2pq)*q2*(1/2) + q4] = p2/(1 -p2) = 99 Kommentarer til det fundne resultat: De syge individer er som regel afkom efter normale forældre, derfor vil selektion mod den recessive kun langsomt fjerne sygdommen. 4 Genfrekvensen findes ved hjælp af kvadratrods-metoden q(r) = 0,6. a) Gravhunde der må antages at være anlægsbærere = 2pq*N = 48. b) Sandsynligheden for at den første hvalp bliver korthåret efter sammenparring af to tilfældigt valgte ruhårede hunde (5/7)2*(1/4) = 0,13. 5 Ved en kønsbunden recessiv egenskab er genfrekvensen lig med fænotype- frekvensen hos hankøn a) Hæmophili blandt mænd q(h) = 1/10000 = 10-4. b) Hæmophili blandt kvinder q2 = (1/10000)2 = 10-8. Heraf ses, at mænd får hæmophili med langt større hyppighed end kvinder. 6 Moderen har blodtype BB eller B0 og faderen blodtype AA eller A0, men da de har et barn med blodtype 0, er deres blodtyper B0 og A0. Deres eventuelle fremtidige børn kan få blodtyperne A0, B0, AB eller 0. 7 a) Frekvensen af genet for henholdsvis rød og sort farve beregnes efter gentælle metoden. p(rød) = (13655+678/2)/14345 = 0,97553 q(sort)= (12 +678/2)/14345 = 0,02447 b) Undersøg ved en Chi-i-anden test, om de observerede antal stemmer overens med de forventede under Hardy-Weinberg ligevægt. Genotyper sorte intermediære røde Observeret 12 678 13655 Forventet 8,58 684.82 13651,58 Chi-i-anden 1,36 0,07 0,00 = 1,43 Det forventede antal er beregnet på grundlag af de estimerede parametre p, q og N. q er en funktion af p, derfor er der anvendt to frie parametre til beregning af forventet antal. Antal frihedsgrader er derfor lig med 3 - 2 = 1. Der er ikke statistisk signifikant afvigelse fra H-W ligevægt. Signifikansgrænse med df=1 er 3,84. 8 a) Genotyperne er angivet ved deres allelnumre, og de forventede frekvenser er anført for hvert locus. Genotyper locus A locus B 1/1 0,01 0,04 1/2 0,06 0,12 1/3 0,12 0,20 2/2 0,09 0,09 2/3 0,36 0,30 3/3 0,36 0,25 b) Forventede frekvens i populationen af genotypen A1A2B1B2 er 0,06 * 0,12 og af genotypen A3A3B3B3 er 0.36 * 0,25 En hanhund med genotypen A1A2B1B2 parres med et antal tæver med genotypen A3A3B3B3. c) Forventede genotyper blandt afkom efter nævnte parringer når de to loci ikke er genetisk koblede og deres frekvens er følgende: A1A3B1B3 er 0,25 A1A3B2B3 er 0,25 A2A3B1B3 er 0,25 A2A3B2B3 er 0,25 d) Forventede genotyper blandt afkom efter nævnte parringer når de to loci er genetisk koblede (c=0,2) og deres frekvens er følgende: A1A3B1B3 er 0,40 A1A3B2B3 er 0,10 A2A3B1B3 er 0,10 A2A3B2B3 er 0,40 9 a. Haplotype NE : 0,3 Haplotype Ne : 0,1 Haplotype ne : 0,6 b. Frekvensen af grise som er modtagelige for ødemsyge stiger. Samtlige ne/ne grise fjernes, Frekvensen af disse er 0,6x0,6 = 0,36, dvs 36% af grisene fjerne ved denne selektion. Resten af grisene fordeler sig som følger: 9% NE/NE, 6% NE/Ne, 36% NE/ne, 1 % Ne/Ne, 12% Ne/ne Haplotypefrekvenserne bliver herefter: Haplotype NE : (2x9 + 6 + 36)/2x64 = 0,4688 Haplotype Ne : (6 + 2x1 + 12)/2x64 = 0,1563 Haplotype ne : (36 + 12)/2x64 = 0,375 Bemærk! Efter selektion vil der være 79,69% grise som er modtagelig for ødemsyge. Før selektion var tallet 51% c. Grise med haplotypen Ne skal selekteres. Dette kan gøres ved at selektere for grise med genotypen N/N e/e eller ved at bruge genotypning i grisefamilier med mindst 3 generationer, så koblingsfasen kan fastlægges og herved kan grise med Ne haplotypen identificeres. Over generationer vil koblingsuligevægten mellem N og E nærme sig nul og det vil blive lettere at identificere individer med den favorable haplotype. 10 a) Koblingsuligevægten D = f(AB) - pA*pB = 0,4 - 0,5*0,6 = 0,10 b) I hver generation reduceres D med 1-c. Generation 0 1 2 3 4 5 6 7 8 9 -------------------------------------------------- D 0,10 0,07 0,05 0,03 0,02 0,02 0,01 0,01 0,01 0,00 c) Genfrekvenserne er konstante gennem generationerne og ved koblingsligevægt er: f(AB) = pA*pB = 0,5*0,6 = 0,30. f(Ab) = pA*qb = 0,5*0,4 = 0,20. f(aB) = qa*pB = 0,5*0,6 = 0,30. f(ab) = qa*qb = 0,5*0,4 = 0,20. d) Hyppigheden af dobbelt-heterozygoter i udgangspopulationen er. 2(f(AB)*f(ab) + f(Ab)*f(aB)) = 2(0,4*0.3 + 0,1*0,2) = 0,28 Ved koblingsligevægt 2(f(AB)*f(ab) + f(Ab)*f(aB)) = 2(0,3*0.2 + 0,3*0,2) = 0,24
Løsninger, Lektion 3, link opgaver
1 a) p(A)=0,4944 og q(a)=0,5056
Populationen er i Hardy-Weinberg ligevægt, da Chi-i-anden er
mindre end 0,1. Signifikansgrænse med df=1 er 3,84.
b) Genfrekvenserne i næste generation med saa = 0,1 bliver:
q' = [(1/2)*0,500 + 0,256*(1-0,1)]/(1-0,256*0,1) =
eller [(1/2)* 225 + 115*(1-0,1)]/(450-115*0,1) = 0,4926
q2 = 0.4799
q3 = 0.4677
q4 = 0.4558
q5 = 0.4442
2 Inden for SDM elimineres rødbrogede kalve fuldstændigt fra hver ny
afkomsgeneration.
a) En halvering af genotypefrekvensen af ee svarer til, at genfre-
kvensen sænkes fra 0,2 (4 % røde kalve) til 0,1414
(2 % røde kalve)
n = 1/0,1414 - 1/0,2 = 2,07
b) n = 1/0,01414 - 1/0,02 = 20,7
c) Forholdet mellem svarene i b) og c) er at det tager 10 gange så
lang tid at halvere frekvensen af røde kalve, når genfrekvensen
er 10 gange lavere. Ved lav frekvens har selektion mod den
recessive ringe effekt.
3 s1 = 0,2 og s2 = 0,7
a) Genfrekvensen q(hat) ved ligevægt
= s1/(s1 + s2) = 0,2/(0,2 + 0,7) = 0,22
b) Genotypefrekvenserne ved ligevægt forud for selektion:
Genotyper A1A1 A1A2 A2A2
Frekvens 0,61 0,34 0,05
c) Genotype-proportionerne efter selektion.
Proportion 0,61*0,8 0,34 0,05*0,3 sum = 0,843
Relativ frekvens 0,58 0,40 0,02
4 s1 = 0,2 og s2 =0,9
a) Frekvensen, q(hat), af Hbs ved ligevægt er 0,2/(0,2+0,9) = 0,18
b) Frekvensen af nyfødte med seglcelleanæmi vil falde, da recessive
ved ligevægt er 0,182 = 0,0324 er mindre end de nuværende 0,05.
5 a) Frekvensen af sygdomsgenet p(C) = (10/2)/94.000 = 5,32*10-5
b) Fertiliteten af dværgene (Cc) 27/108 = 0,25
Fertiliteten af normale (cc) 582/457 = 1,27
Dværge relativt 0,20
c) Skøn for mutationsfrekvensen c til C.
my = p*s = 5,32*10-5*0,80 = 4,26*10-5
6 Variansen på genfrekvensen regnes som en binominalvarians over udfald,
2N = 80. Variansp = 0,6*0,4/80 svarende til en spredning på 0,0548.
Sikkerhedsgrænserne for p svarende til en sandsynlighed på 5% bliver
0,6 plus/minus 2*0,0548 svarende til at genfrekvensen i generation 1 vil
ligge mellem 0,49 og 0,71.
7 a) 1/Ne = (1/4)*(1/5 + 1/50) svarende til Ne = 18,18
dvs. 9 hanner + 9 hunner
b) Stigningen i indavlsgraden pr. generation i de to populationer
er delta F = 1/(2*18,18) = 2,75 %
Løsninger, Lektion 4, link opgaver
1 For at beregne indavlskoefficienten reducerer man diagrammet,
så kun de relevante individer er med. Da ingen af individerne
A, B, C og D har fælles aner, kan ingen gener nå frem til X
i dobbelt dosis. X er ikke indavlet, da dets forældre E og G
ikke er beslægtede.
2 De indavlede individer er C, D og E.
aAB = 1/2 og FC = aAB/2 = 1/4
da A er fælles ane for de to forældre.
aBC = 1/2 + 1/4 og FD = aBC/2 = 3/8
da A og B er fælles ane for de to forældre.
aCD = 1/2(1+1/4) + 1/4 + 1/8 og FE = aCD/2 = 1/2
da A, B og C er fælles ane for de to forældre og C er indavlet.
eller med tabularmetoden
Forældre - 1 - 1-2 3-2 3-4
Dyr nr. 1=A 2=B 3=C 4=D 5=E
-----------------------------
1 1 1/2 3/4 5/8 11/16
2 1/2 1 3/4 7/8 13/16
3 3/4 3/4 1+1/4 1 9/8
4 5/8 7/8 1 1+3/8 19/16
5 11/16 13/16 9/8 19/16 1+1/2
Og her kan blive udledt en formel for indavl baseret på indavlen i
to tidligere generationer
F5 = a34/2 = (a32+a33)/4 = (2F4 + 1 + F3)/4
3 a) Opstil et pilediagram for individet A.
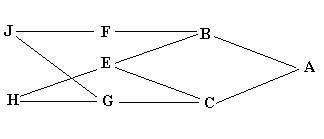
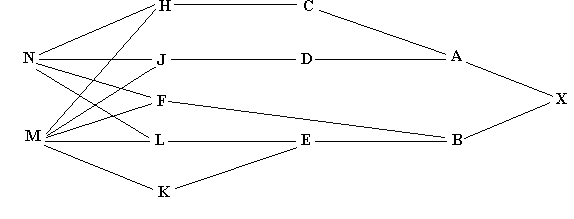
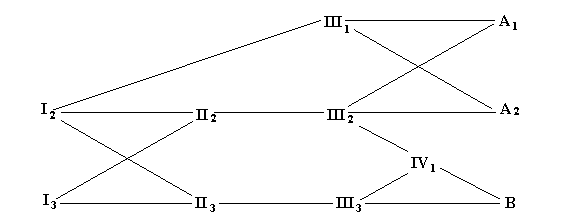
Løsninger, Lektion 5, link opgaver
1 a) IV 1 og IV 4 er aa.
III 4 og III 8 er Aa da de får afficeret afkom.
II 2 og II 5 er Aa da II 1 og II 6 er AA.
b) Frekvensen af heterozygoter blandt fænotypisk normale
individer efter heterozygotiske forældre er
p(Aa | aa) = p(Aa)/(1-p(aa)) = (1/2)/(1 - (1/4)) = 2/3.
2 Kønsbunden dominant: Udelukket
Kønsbunden recessiv: Kan forekomme
Autosomal dominant: Udelukket
Autosomal recessiv: Kan forekomme
Kønsbunden recessiv er den mest sandsynlige arvegang, idet kun I 2
og II 2 skal være heterozygote, mens en autosomal recessiv arvegang
kræver at I 1, I 2, II 2 og III 1 er heterozygoter. Dominant arvegang
kan udelukkes, da ingen af forældrene i generation I er afficerede.
3 Kønsbunden dominant: Udelukket, idet II 7 skulle være afficeret.
Kønsbunden recessiv: Udelukket, idet III 3 og III 6 ikke kan være
være afficerede med mindre II 4 er det.
Autosomal dominant: Sandsynlig.
Autosomal recessiv: Kan ikke udelukkes.
En autosomal recessiv arvegang kræver at I 1, II 1 og II 4 er
heterozygoter, hvorimod autosomal dominant arvegang ikke stiller
nogen krav. Derfor må en autosomal dominant arvegang anses for
at være den mest sandsynlige.
4 Kønsbunden dominant: Arvegang er mulig.
Kønsbunden recessiv: Kan udelukkes, idet III 4 er almindelig.
Autosomal dominant: Arvegang er mulig.
Autosomal recessiv: Er ikke sandsynlig, idet I 2 og II 4 så skal være
heterozygote.
En han fra generation III med den nye pelskvalitet parres med
hunner med almindelig pels. Udspaltningen vil vise arvegangen.
5 En kønsbunden recessiv mutant vil først vise sig hos det hetero-
gametiske køn.
1) Høns høner (ZW kønskromosomer)
1) Kaniner hanner (XY kønskromosomer)
6 a) Det testes, om tyren er AA eller Aa, da den er mistænkt for at
være anlægsbærer.
Metode: Da den danske population udelukkende er AA, skal der
anvendes testparringer med egne døtre, som enten er AA (50%)
eller Aa (50%).
b) P(afficeret individ, dvs aa) = 1/8, P(normalt individ) = 7/8.
P(n normale individer) = (7/8)n, dvs. n findes ud fra
at (7/8)n = 0,05 ved en signifikansgrænse på 5%.
n = 23 stk afkom
c) Hvis der blandt de 23 stk afkom ikke er nogen med genotypen aa
(afficerede), kan det med 95% sikkerhed siges, at tyren ikke er
anlægsbærer (Aa) og derfor må være AA.
7 Der anvendes signifikansgrænse på 5%
1) P(n normale afkom) = (1/2)n = 0,05; n = 5 stk.
2) P(n normale afkom) = (3/4)n = 0,05; n = 11 stk.
3) P(n normale afkom) = (7/8)n = 0,05; n = 23 stk.
8 I spørgsmål b og c skal der tages hensyn til at I 2 og II 2 ikke er
af genotypen nn.
a) I 1 og II 1 er anlægsbærere for halotangenet n. Sandsynligheden
for at henholdsvis III 1, III 3 og III 5 er anlægsbærere er 2/3,
da de er normale og derfor kommer fra en fordeling på 1:2.
b) q = 0,2 og P(I 2 er Nn | den ikke er nn)
= 2*0,2*0,8/( 1-0,04) = 0,3333
c) P(III 6 er NN | den ikke er nn)
= ((1/2)*(1-0,3333/2))/(1-(1/2)*0,3333/2) = 0,455
9 Forventningen blandt afkom efter heterozygotiske forældre er 1:2:1,
derfor bliver Chi-i-anden beregningen med df=2
(39-30)2/30 + (51-60)2/60 + (30-30)2/30 = 4,05
Da Chi-i-anden værdien er mindre end tabelopslag for 5 % (5,99) er der
ikke statistisk signifikant afvigelse fra den forventede 1:2:1
udspaltning.
10 Ved en tilbagekrydsning med i alt 30 tilbagekrydsningsindivider kan
udspaltningsforholdet være følgende med tilsvarende Chi-i-anden
beregning.
Aa aa Chi-i-anden
30 0 30
. .
21 9 4,80
----------------------------------------------
20 10 3,33
. .
15 15 0 non-signifikant område
. .
10 20 3,33
----------------------------------------------
. .
0 30 30
Da df=1 kan hypotesen om recessiv nedarvning accepteres, med alle et
Chi-i-anden på mindre end 3,84 (5% signifikansgrænsen), dvs. en
udspaltning på mellem 10 til 20 eller op til det omvendte 20 til 10.
Løsningen på ligningen
chi-i-anden = (x-15)2/15 + ((30-x)-15)2/15 = (2/15)x2 + 4x2 + 30 = 3,84
er 20,37 og 9,63.
11 En kønsfordeling på to hanner og fire hunner i et kuld minkhvalpe
på seks stk. er binomialfordelt og har en sandsynlighed på
K6,2*(1/2)2*(1/2)4 = (6*5)/(2*1) * (1/64) = 0,23
12 Sandsynligheden for at en heterozygotisk ko får én kullet + tre hornede
kalve efter inseminering med heterozygotiske tyre er
K4,1*(3/4)1*(1/4)3 = 12/256 = 0,05
13 De mulige kombinationer af AA, Aa og aa i familier på tre søskende efter
parring mellem heterozygotiske forældre.
AA Aa aa
------------------
3
3
3
2 1
1 2
2 1
1 2
2 1
1 2
1 1 1
------------------
14 Der anvendes Chi-i-anden test, da der er tale om testparring
for udspaltningsforhold 3:1 med en hypotese om recessiv nedarvning.
Der er ialt 33 normale og 8 afficerede og Chi-i-anden bliver
(33-30,75)2/30,75 + (8-10,25)2/10,25 =0,66
Df=1, der er ikke statistisk signifikant afvigelse fra det forventede
ved en 3:1 udspaltning.
15 Undersøgelsen om udspaltningen af recessive i nærværende familie-
materiale hos kvæg om overensstemmelse med en 7:1 spaltning må gennem-
føres efter Singles metode, da familierne er fundet på grundlag af
mindst et afficeret afkom.
Total antal T=53
Antal afficerede A=13
Antal familier med 1 afficeret afkom A1=9
Antal familier med 2 afficerede afkom A2=2
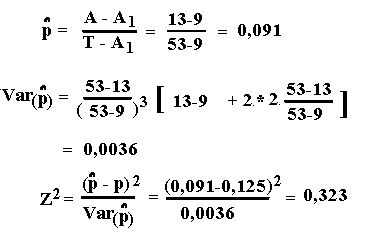
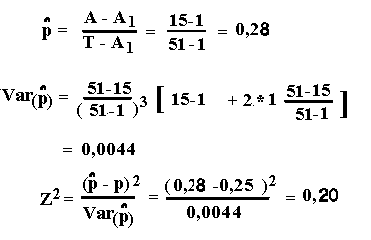
Løsninger, Lektion 6, link opgaver
1 p(Rd) og q(rd) er henholdsvis 0,7 og 0,3. Det gennemsnitlige riboflavinindhold pr. gram blomme er (summen af genotypefrekvens*værdi): 0,49*4,30 +0,42*2,50 + 0,09*0,40 = 3,19 2 a) Gennemsnitsfrekvensen for populationen er: 0,64 * 0,008 + 0,32*0,016 + 0,04 *0,020 = 0,0110 b) De tre genotypiske værdiers afvigelser fra populationsgennemsnittet AA 0,020 - 0,0110 = 0,0090 Aa 0,016 - 0,0110 = 0,0050 aa 0,008 - 0,0110 = -0,0030 c) Genotypeværdiernes (G) opdelt i en additiv del (A=avlsværdi) og en dominansafvigelse (D). Genotype G = A + D AA 0,0090 = 0,0116 + (-0,0026) AAA = 2(0,2*0,0090 + 0,8*0,0050) Aa 0,0050 = 0,0044 + 0,006 aa -0,0030 =-0,0028 + (-0,0002) Aaa = 2(0,2*0,0050 + 0,8*-0,0030) Avlsværdien bestemmes ved afkommets gennemsnit når en genotype parres tilfældigt i populationen. Dominansafvigelsen bestemmes som en rest. 3 Respons ved individuel selektion måles som: R = h2(SFædre + SMødre)/2 Indsættes i formel får man: (89,5-88,5) = h2((102-88,5) + (93-88,5))/2 og h2 = 0,11 4 h2 for smørfedtydelse beregnes p.g.a formel for selektionsrespons. R = h2(SFædre + SMødre)/2 R1 = h2(SFar + S1)/2 R2 = h2(SFar + S2)/2 ved subtraktion af de to formler får man: R1 - R2 = h2(S1 - S2)/2 266-259 = h2(295-227)/2, idet alle tal skal måles som afvigelse fra gennemsnit h2 = 0,21 5 Pilediagrammer over relationen mellem halvsøskende, mellem helsøskende og forældre-afkom.Den forventede fænotypiske korrelation mellem halvsøskende, mellem helsøskende og mellem forældre og afkom. Korrelationen halvsøskende r =(1/4)h2 helsøskende r =(1/2)h2 + c2 forældre-afkom r =(1/2)h2 6 På grundlag af et større observationssæt er der beregnet korrelation mellem beslægtede individer for vægt ved 6 uger hos grise. Resultaterne var følgende: Korrelationen halvsøskende r =(1/4)h2 = 0,05 helsøskende r =(1/2)h2 + c2 = 0,25 svarende til h2 halvsøskende = 0,20 c2 helsøskende = 0,15 h2 beregnet på helsøskendematerialet bliver 0,5, men da den beregnede på halvsøskendematerialet kun bliver 0,2, må der for helsøskende være en fælles miljø-komponent. Den fælles miljø-komponent for helsøskende kan tilskrives det maternelle miljø for kuldet. 7 På grundlag af et observationssæt er der beregnet korrelation og regression mellem beslægtede individer for højde hos veterinær- studerende. Resultaterne var følgende: Korrelationen mor-afkom r =(1/2)h2 = 0,45 far-afkom r =(1/2)h2 = 0,20 Regression afkom-gns. forældre b = h2 = 0,65 Korrelationerne svarer til h2 mor-afkom = 0,90 h2 far-afkom = 0,40 h2 beregnet på mor-afkom bliver meget høj, 0,90, i forhold til den beregnede på far-afkom, der kun bliver 0,40. Det kan tyde på at der er en fælles miljø-komponent for mor og afkom. Den lave værdi på far- afkom kan evt. tilskrives ukorrekt faderskab. Regression afkom på gns. forældre har været meget konstante gennem tiderne siden de første beregninger blev gennemført for mere end 100 år siden.
Løsninger, Lektion 7, link opgaver
1 Der anvendes formel for avlsværdiindeksets kvadrede sikkerhed.
n*h2*a'2/(1 + (n-1)(a*h2 +c2))
a'=1/2 a= - for moderens præstation rAI = 0,25
a'=1/4 a=1/4 for 50 halvsøskendes præstation rAI = 0,44
a'=1/2 a=1/4 for 20 stk. halvsøskende-afkom rAI = 0,76
Den største sikkerhed fås ved at måle 20 stk. halvsøskende-afkom.
2 Der anvendes formler fra kompendium for avlsværdi og sikkerhed.
1) egen ydelse 1. laktation, a'=1 a=-
4500 + [(1*0,25*1)/(1+0)]*(5000-4500) = 4625 kg; rAI = 0,50
2) gns. af egen ydelse i tre laktationer, a'=1 a=1
4500 + [(3*0,25*1)/(1+2(,25+,05))]*(4700-4500) = 4594 kg; rAI = 0,68
3) gns. af moderens ydelse i tre laktationer, a'=1/2 a=1
4500 + [(3*0,25*,5)/(1+2(,25+,05))]*(5000-4500) = 4617 kg; rAI = 0,34
4) gns. af 100 paternelle halvsøskende, a'=1/4 a=1/4
4500 + [(100*0,25*,25)/(1+99*,25*,25)]*(4600-4500) = 4587 kg; rAI=0,47
5) både 3) og 4), se formel afsnit 7.4
(på basis af forældres avlsværdi og sikkerhed).
(4617 + 4587)/2 = 4602 kg;
rAI = kvadratrod[(0,342+0,472)/4] = 0,29
Avlsværdiindekset for egenydelse i 3 laktationer er beregnet med størst
sikkerhed.
3 Egenskaben behandles som en tærskelegenskab med værdierne 0 og 1.
a) Populationsgennemsnittet for tærskelegenskaben OCD hos svenske
sportsheste er 0,7 og gennemsnittet for de 3 afkomsgrupper
er A 0,5, B 0,75 og C 0,80
b) De tre hingstes avlsværdiestimat vurderet på halvsøskende-afkom,
a'=1/2 a=1/4
Hingsten A har 40 stk. afkom, af hvilke 20 er OCD fri.
0,7 + [(40*0,20*,5)/(1+39(,20*,25))]*(0,5-0,7) = 0,43
Hingsten B har 60 stk. afkom, af hvilke 45 er OCD fri.
0,7 + [(60*0,20*,5)/(1+59(,20*,25))]*(0,75-0,7) = 0,78
Hingsten C har 20 stk. afkom, af hvilke 16 er OCD fri.
0,7 + [(20*0,20*,5)/(1+19(,20*,25))]*(0,8-0,7) = 0,80
4 Sikkerhed kvadreret ved avlsværdiberegning i de 5 tilfælde:
h2 0,05 0,1 0,2 0,4 0,6
-------------------------------------------
1) 0.05 0.10 0.20 0.40 0.60
2) 0.15 0.27 0.45 0.66 0.78
3) 0.17 0.20 0.22 0.23 0.24
4) 0.11 0.20 0.34 0.52 0.63
5) 0.71 0.83 0.91 0.95 0.97
Heritabilitetens størrelse har mindre betydning for
avlsværdiindekset sikkerhed, når der er mange målinger, end
ved færre målinger.
5 Formel for avlsværdi indeks og sikkerheden kvadreret for individer
med information fra, populationsgennemsnittet betegnes P,bar:
1) egen præstation (P) og a'=1 a= -
P,bar + [(1*h2*a')/(1 + 0*( ))]*(P -P,bar)
= P,bar + h2 *(P -P,bar)
r2AI = h2
2) de to forældres præstationer (P,gns) og a'=1/2 a= 0 n=2
P,bar + [(2*h2*a')/(1 + 1*(0))]*(P -P,bar)
= P,bar + h2 *(P,gns -P,bar)
r2AI = h2/2
3) de fire bedsteforældres præstationer (P,gns) og a'=1/4 a=0 n=4
P,bar + [(4*h2*a')/(1 + 3*(0))]*(P -P,bar)
= P,bar + h2 *(P,gns -P,bar)
r2AI = h2/4
4) de otte oldeforældres præstationer (P,gns) og a'=1/8 a=0 n=8
P,bar + [(8*h2*a')/(1 + 7*(0))]*(P -P,bar)
= P,bar + h2 *(P,gns -P,bar)
r2AI = h2/8
Resultaterne viser, at forventningen til avlsværdien er den samme
i de fire tilfælde, men sikkerheden falder drastisk jo længere man
kommer ud i stamtavlen.
Løsninger, Lektion 8, link opgaver
1 Respons ved individuel selektion måles som: R = h2(SFædre + SMødre)/2 Indsættes i formel får man R = 0,3[(1008-935) + (970-935)]/2 = 16 gram Den gennemsnitlige tilvækst der forventes for afkommet er 935 + 16 = 951 gram. 2 Ved tabelopslag findes 'i' når der bruges 5% hanner til avl er i = 2,06 og 33% hunner til avl er i = 1,10 S beregnes som i*sigmaP for hanner til 2,06*0,3 = 0,618 og hunner til 1,10*0,2 = 0,220 Den genetiske ændring i krops størrelse man forventer pr. generation R = 0,4(0,618 + 0,220)/2 = 0,17 kg 3 Det antages, at en population af høner har en årlig gennemsnitsydelse på 230 æg. Den fænotypiske standardafvigelse er 35,7 æg. Der regnes endvidere med en heritabilitet på 0,40 for årlig ægydelse. Selektionen baseres udelukkende på høner, og 20 procent af de højestydende høner benyttes til avl. Beregn følgende: a) Selektionsdifferencen (antal æg) er i*sigmaP = 1,4*35,7 = 50 'i' er funden ved tabel opslag. b) Den genetiske ændring (antal æg) fra moder til datter- generationen. R = 0,4(0 + 50)/2 = 10 æg c) Døtrenes gennemsnitlige ægydelse pr. år forventes at blive: 230 + 10 = 240 æg 4 Hoftedysplasi hos hunde er en tærskelegenskab med en heritabilitet på h2 = 0,3. Ca. 30% af alle Schæferhunde har hoftedysplasi. De 70%, der er fænotypisk raske, har tilsyneladende ens avlsværdi, hvis man udeluk- kende baserer avlsværdien på grundlag af røntgenbilleder af de pågældende hunde. a) Når der blandt de 70% raske Schæferhunde udtages en tilfældig stikprøve, svarer det til at der udtages 70% til avl: i=0,50 b) Når man anvender de 70% raske Schæferhunde til avl bliver: delta G = i*h2*sigmaP = 0,5*0,3*sigmaP = 0,15 sigmaP-enheder c) Når der bruges 10% hanner til avl er i= 1,75, og 70% hunner til avl er i= 0,5. VA = VP*h2svarende til sigmaA = 0,55*sigmaP rAI = 0,79 delta G = (1,75*,79*,55*sigmaP + 0,15*sigmaP)/2 = 0,46*sigmaP d) Forholdet mellem delta G beregnet under punkt c) og b) er: En forbedring på 3 gange. 5 Antal afkom pr. fader der skal afprøves optimeres så den genetiske ændring pr. generation er størst mulig. Da stationen har en bestemt størrelse og der skal bruges et bestemt antal til avl, er det forholdet mellem intensitet og sikkerhed, der skal optimeres. Der opstilles en tabel der har gruppestørrelse (n) som variabel. n til avl i * rAI -------------------------------------------- 1 40/800 2,06 * 0,224 = 0,461 2 40/400 1,76 * 0,308 = 0,540 3 40/266 1,58 * 0,369 = 0,583 4 40/200 1,40 * 0,416 = 0,583 5 40/160 1,28 * 0,456 = 0,584 6 40/133 1,16 * 0,490 = 0,568 7 40/113 1,07 * 0,519 = 0,555 F.eks. for n=4 kan der testes 200 hanner heraf skal der bruges 40 til avl, hvilket svarer til 20%, der ved opslag giver i=1,40. Det bedste resultat fås for n lig 5, men toppunktet er meget fladt. 6 a) Der er to fænotyper der kan tilskrives værdierne 0 og 4, hvilket svarer til den nævnte effekt. Da der er fuldstændig dominans, er frekvensen af de to fænotyper 0,25 og 0,75, hvilket svarer til en middelværdi på 3. Varians beregnes som de vægtede afvigelsers kvadrat: 32*0,25 + 12*0,75 = 3.0 Genets bidrag til den samlede additive varians er 3 procent b) Kommentarer til hvornår det er formålstjenligt at anvende genmar- kører: Andel af egenskabens additive varians skal være ret stor, meget større end de tre procent i nærværende tilfælde. Heritabiliteten for egenskaben skal endvidere være lav, dvs. af størrelsorden 10 % eller mindre. 7 a) Ved et selektionseksperiment med mus kan den genetiske korrelation mellem tilvækst og kuldstørrelse beregnes som forholdet mellem de standardiserede direkte og indirekte selektionsrespons: rAx,Ay = (0,693/0,88)/(2,34/1,13) = 0,38 idet sigmaAx = 1,13 og sigmaAy = 0,88 b) Selektionsintensiteten ix beregnes ved hjælp af formlen for delta G, den gælder for selektion over en generation. Derfor skal R divideres med 9. R = S*h2 = h2*i*sigmaP = 2,34/9 gram, svarende til i=0,48
Løsninger, Lektion 9, link opgaver
1 a) Indavl reducerer frekvensen af heterozygoter og øger tilsvarende frekvensen af homozygoter i forhold til H-W ligevægt. Den gennemsnitlige vægt under indavl på F=0,25 og Fpq=0,04 er: 100*(,64+Fpq) + 80*(,32-2Fpq) + 50*(,04+Fpq) = 91,2 gram b) Den gennemsnitlige vægt uden indavl er: 100*,64 + 80*,32 + 50*,04 = 91,6 gram Indavlsdepressionen er 0,4 gram 2 a) Graden af heterosis ved krydsninger er i procent: 1) ikke-indavlede 100*(22,8-(22,7+20,1)/2)/((22,7+20,1)/2)= 6,5% 2) indavlede 100*(19,9-(21,7+13,1)/2)/((21,7+13,1)/2)= 12,6% b) Indavlsdepressionen er nedgang i middelværdi ved indavl. Indavlsdepressionen udtrykt i procent for: linie A 100*(22,7-21,7)/22,7 = 4,4% linie B 100*(20,1-13,1)/20,1 = 34,8%
Standpunkts test: Lektion 2 . Vælg det rigtige alternativ! |
Rigtige svar cbadbc |
| 1) Hvad indebærer Hardy-Weinberg loven?
a.At populationen er lille b. At genfrekvensen vil stige c. At genfrekvensen er konstant over generationer d. At genotypefrekvensen er uafhængig af genfrekvensen e. Ingen af alternativerne |
2) Hvordan beregnes genfrekvensen?
a.Optælling af alle alleler i populationen b. Det relative antal af en given allel c. Summen af alle homozygoter d. Antal af en given allel e. Ingen af alternativerne |
| 3) Hvordan beregnes forventet genotypefrekvens?
a.Ved h. a.sandsynlighedsregningens additions og multiplikationsregel b. Ved at lægge fædrens og mødrens genfrekvenser sammen c. Ved at optælle antallet af en given genotype d. Ved at anvende en DNA test e. Ingen af alternativerne |
4) Hvilken udspaltning kan ikke chi-i-anden-testes for H-W
-ligevægt?
a.Codominante arveanlæg b. Kønsbundne arveanlæg c. Når der er mere end to alleler d. Dominante arveanlæg med to alleler e. Ingen af alternativerne |
| 5) Hvad betyder kobling?
a.At generne er i samme kønscelle b. At generne sidder på samme kromosom c. At generne sidder på to forskellige kromosomer d. At der kan beregnes en gamet frekvens e. Ingen af alternativerne |
6) Hvad er en gamet frekvens?
a.Det samme som genfrekvens b. Indholdet af gener i en gamet c. Frekvensen af en kombination af alleler på flere loci d. Frekvensen af en kombination af alleler på flere loci, der er koblede e. Ingen af alternativerne |
Standpunkts test: Lektion 3. Vælg det rigtige alternativ! |
Rigtige svar abeebc |
| 1) Hvad er den stærkeste faktor for ændring af genfrekvens
i naturlige populationer?
a.Populationen er lille b. Mutation c. Selektion d. Ikke tilfældig parring e. Tilfældig parring |
2) Genfrekvensen efter selektion kan beregnes som:
a.Optælling af alle alleler i populationen b. Det relative antal af en given allel efter selektion c. Summen af alle homozygoter d. Antal af en given allel e. Ingen af alternativerne |
| 3) Hvordan er fitness defineret?
a.Som overlevelseschance for en heterozygot b. Som forholdet mellem antallet af homozygoter og heterozygoter c. Summen af homozygoter d. Ved at anvende en DNA test e. Ingen af alternativerne |
4) Hvad betyder overdominans for fitness?
a.At homozygote individer er mest levedygtige og producerer mest afkom b. At heterozygote individer er mest levedygtige c. At antallet af heterozygote er afhængigt af antal alleler d. Dominante arveanlæg med to alleler e. Ingen af alternativerne |
| 5) Hvad betyder 'genetic load'?
a.At visse alleler giver dårligere overlevelseschancer b. Det relative antal, der bortfalder på grund af selektion c. At dyrene fungerer dårligt d. At der kan beregnes fitness e. Ingen af alternativerne |
6) Hvilket af følgende gælder for en lille population?
a.Allel frekvensen falder b. Der er ikke tilfældig parring c. Variansen på allel frekvensen er stor d. Individernes fitness stiger e. Ingen af alternativerne |
Standpunkts test: Lektion 4 . Vælg det rigtige alternativ! |
Rigtige svar cdec |
| 1) Hvordan er indavl defineret?
a.Avl mellem helsøskende b. Stigende homozygotigrad c. Identisk homozygoti på grund af afstamning d. Ikke tilfældig parring e. Ingen af alternativerne |
2) Hvordan er additiv slægtskab defineret?
a.Som summen af slægtskaber mellem to dyrs forældre b. Det relative antal gener der er identiske hos to dyr c. Summen af alle homozygoter hos to dyr d. Det relative antal gener der er identiske hos to dyr på grund af afstamning e. Ingen af alternativerne |
| 3) Hvad er det additive slægtskab mellem to halvsøskende?
a.0,5 b. 0,30 c. 0,20 d. 0,10 e. Ingen af alternativerne |
4) Hvilken betydning har indavl?
a.At homozygote individer bliver mere levedygtige b. At heterozygote individer bliver mere levedygtige c. At der sker en stigning i antal homozygoter d. At der sker en stigning i antal heterozygoter e. Ingen af alternativerne |
Standpunkts test: Lektion 5. Vælg det rigtige alternativ! |
Rigtige svar cdadda |
| 1) Hvad er en proband?
a.Et dyr der er sygt b. Et dyr der er normal i en familie med syge c. Et dyr der giver anledning til en undersøgelse d. Et dyr med en recessiv lidelse e. Ingen af alternativerne |
2) Ved kønsbunden dominant nedarvet sygdom
a.Der er samme frekvens hos begge køn b. Hos pattedyr er frekvensen højest hos hanner c. Hos fjerkræ er frekvensen højest hos haner d. Forholdet er 2:1 mellem kønnene hos pattedyr e. Ingen af alternativerne |
| 3) Hvad er den forventede frekvens af recessive
anlægsbærere?
a.Populationsfrekvensen af heterozygoter b. Populationsfrekvensen af heterozygoter minus homozygote recessive c. Udspaltningsforholdet er 0,25, der samtidig er frekvensen d. Frekvensen er lig mutationsraten e. Ingen af alternativerne |
4) Hvad opnås ved at anvende Singles korrektion?
a.At der korrigeres for dominansforhold b. At der korrigeres for overlappende generationer c. At der korrigeres for antal alleler d. At der korrigeres for familier uden udspaltning e. Ingen af alternativerne |
| 5) Testparring anvendes for at teste om
a.to dyr er i familie b. to gener er koblede c. egenskab nedarves som tærskelegenskab d. egenskab nedarves som en simpel Mendelsk egenskab e. Ingen af alternativerne |
6) Hvor opstår en 1 til 7 udspaltning?
a.Hos afkom efter fader datter parring b. Hos afkom efter helsøskende parring c. Hos afkom efter halvsøskende parring d. Hos afkom efter parring af kendte bærere e. Ingen af alternativerne |
Standpunkts test: Lektion 6 . Vælg det rigtige alternativ! |
Rigtige svar bddcbc |
| 1) I hvilke enheder måler man geneffekten for en
kvantitativ egenskab?
a.Den måles som afvigelse fra gennemsnittet b. Enheden på den skala hvori egenskaben måles c. Enheden er afhængig af om der er dominans d. Der måles i kilogram e. Ingen af alternativerne |
2) Hvorledes måles genotypen for en kvantitativ egenskab?
a.På samme måde som i kvalitativ genetik b. Det er normalt ikke mulig at måle genotypen c. Genotypen er lig med phenotypen d. Som den gennemsnitlige phenotypiske værdi e. Ingen af alternativerne |
| 3) Hvordan defineres avlsværdi?
a.Som et dyrs phenotypeværdi b. Som Genotypeværdi + Dominansafvigelse c. Ved at optælle alle individer med samme genotype d. Ved h. a.et dyrs afkom e. Ingen af alternativerne |
4) Hvordan er heritabiliteten defineret?
a.Som forholdet mellem additive gener og dominante gener b. Som summen af dominante arveanlæg c. Som forholdet mellem additiv og phenotypisk varians d. Som summen af additive arveanlæg e. Ingen af alternativerne |
| 5) Hvordan beregnes skøn for heritabilitet?
a.Ved korrelation mellem slægtninge i forhold til slægtskabskoefficienten b. Som forholdet mellem genetisk korrelation og phenotypisk varians c. Ved korrelation mellem halvsøskende d. Ved h. a.chi-i-anden test e. Ingen af alternativerne |
6) Hvilken datatype er bedst til heritabilitets beregning? a.Enægstvillinger b. Feltdata c. Havlsøskende grupper d. Helsøskende grupper e. Forældre afkom |
Standpunkts test: Lektion 7 . Vælg det rigtige alternativ! |
Rigtige svar bcec |
| 1) I hvilke enheder måler man skøn for avlsværdi for en
kvantitativ egenskab?
a.Der måles som afvigelse fra gennemsnittet b. Enheden på den skala hvori egenskaben måles c. Enheden er afhængig af om der er dominans d. Der måles i kroner e. Ingen af alternativerne |
2) Hvad er basismålingen for skøn for avlsværdi?
a.Forældrenes avlsværdi b. Dyrets genotype værdi c. Phenotype målinger d. Den gennemsnitlige phenotypiske værdi af forældre e. Ingen af alternativerne |
| 3) Hvilken af følgende situationer giver størst sikkerhed på
avlsværdi skønet?
a.Måling af et dyrs phenotypeværdi b. Måling af de to forældre c. Måling af 20 helsøskende d. Måling af 20 halvsøskende + begge forældre e. Måling af 100 stk halvsøskende afkom |
4) Hvad er formålet med at beregne avlsværdi skøn?
a.At man kan få udtryk de additive gener b. At man kan få et skøn for et dyrs dominante arveanlæg c. At man kan ligestille dyr med forskellig information før selektion d. At man kan selektere på grundlag af subjektive kriterier e. Ingen af alternativerne |
Standpunkts test: Lektion 8 . Vælg det rigtige alternativ! |
Rigtige svar ecadc |
| 1) Hvad menes med selektions intensitet?
a.Afvigelse fra gennemsnittet af dem der bruges til avl b. Avlsværdi af dem der bruges til avl c. En høj middelværdi d. En stor additiv varians e. Ingen af alternativerne |
2) Hvad er definitionen på delta G ?
a.Gennemsnittet af afkom b. Gennemsnit af afkom af selekterede forældre c. Forskel i gennemsnit mellem forældre og afkoms generationen d. Forskel i gennemsnit mellem population og dem der anvendes til avl e. Ingen af alternativerne |
| 3) Generations intervallet defineres som
a.gennemsnitlig alder når et tilfældigt afkom fødes b. gennemsnitlig alder når første afkom fødes c. gennemsnitlig alder når dyrene udgår af populationen d. gennemsnitlig alder på et givet tidspunkt e. Ingen af alternativerne |
4) Hvordan forekommer en tærskel egenskab?
a.Som summen af additive og dominante gener b. Som summen af dominante arveanlæg c. Som summen af milieumæssige faktorer d. Som summen af genetiske og milieumæssige faktorer e. Ingen af alternativerne |
| 5) Hvilke konsekvenser har genetisk korrelation?
a.Har ingen betydning i et selektionsprogram b. Medfører ændringer i sekundære egenskaber ved selektion c. Påvirker fitness negativt d. Påvirker fitness positivt e. Ingen af alternativerne |
|
Standpunkts test: Lektion 9. Vælg det rigtige alternativ! |
Rigtige svar caedb |
| 1) Hvad menes med indavlsdepression?
a.Forøget udspaltning af recessive arveanlæg ved indavl b. Ændrede udspaltnings forhold ved indavl c. Fald i en egenskabs middelværdi ved indavl d. Fald i en egenskabs additive varians e. Ingen af alternativerne |
2) Hvilken af nedenstående har en lineær relation ?
a.Indavls depression og indavlsgrad b. Relation mellem afkom og en forældre races gennemsnit c. Forskel i gennemsnit mellem forældreracer og afkoms gennemsnit d. Forskel i gennemsnit mellem forældre racer og krydsningsfrodighed e. Ingen af alternativerne |
| 3) Hvilken krydsningstype giver negative rekombinations
effekter?
a.Tovejskrydsning b. Trevejskrydsning c. Tilbagekrydsning d. Rotationskrydsning e. Ingen af alternativerne |
4) Hvordan vedligeholdes en indavlet musestamme?
a.Ved forældre afkom parringer b. Ved koloniavl mellem indavlede dyr c. Ved rotationsavl d. Ved helsøskende parringer e. Ingen af alternativerne |
| 5) Hvordan sikres minnimum indavl i lille population?
a.Ved at føre stamtavle b. Ved at sikre at alle dyr får to stk afkom, der indgår i videre avl c. Ved at avle videre med sunde dyr d. Ved at gennemføre halvsøskende parringer i halvdelen af populationen e. Ingen af alternativerne |
A java interpreter should be enabled in your browser to run the applets
! !
By using the applets a general feature is that you can place your input
in the green fields. The yellow fields can also be used for input, often
in the next round of calculations.
Be careful not to leave any blanks (not visible) in these fields, so
if the applet will not run, test if the cursor stands right next to the
number in all green or yellow fields you have touched.
Applets
2.2 Chi-square test for Hardy-Weinberg equilibrium
2.4 Calculation of mating type frequencies in a H-W population
2.5 Chi-square test for 2 by 2 or 3 by 3 table (eg linkage disequilibrium)
2.5 Linkage, 3-point analyses from test cross
2.5 Many programs for statistical tests, collected by Lowry, USA
2.51 Linkage: Calculation of gamete and genotype frequencies
3.4 Selection: Change in gene- and genotype frequencies
3.5 Change in gene- and genotype frequencies: Effect of population size
4.5 Calculation of relationship and inbreeding coefficients by the tabular method
5.6 Calculation of Chi-square test for deviation from Mendelian ratios
5.7 Calculation of corrected segregation ratio according to Singles method
6.2 Calculation of mean, Genetic and Additive values and Dominance deviations
7.2 Estimating simple forms of breeding values
7.2 Estimating animal model breeding values
8.2 Calculating breeding values and selection response
8.3 Calculating heritability for threshold traits (diseases)
df .20 .10 .05 .02 .01 .001 .0001 ------------------------------------------------------------- 1 1.64 2.71 3.84 5.41 6.63 10.83 15.14 2 3.22 4.61 5.99 7.82 9.21 13.82 18.42 3 4.64 6.25 7.81 9.84 11.34 16.27 21.11 4 5.99 7.78 9.49 11.67 13.28 18.47 23.51 5 7.29 9.24 11.07 13.39 15.09 20.51 25.74 6 8.56 10.64 12.59 15.03 16.81 22.46 27.86 7 9.80 12.02 14.07 16.62 18.48 24.32 29.88 8 11.03 13.36 15.51 18.17 20.09 26.12 31.83 9 12.24 14.68 16.92 19.68 21.67 27.88 33.72 10 13.44 15.99 18.31 21.16 23.21 29.59 35.56
Link to some basic statistical formulas
Other programs
4.4 Calculation of inbreeding coefficients
6.4 Calculation of the heritability by statistical analyses
7.3 Direct updating of breeding values
Applets for handling of matrices.
Bryan Lewis's General Matrix Applet, with added inversion routine
The java language from sun is used to develop the applets, java.sun.com is linked here
- Put your observed numbers and click the Calculate button.
In all coloured cells with initial values you can put data (green fields, two alleles only, yellow fields for a third allele, and blue fields for a fourth allele)
The number of degrees of freedom for the chi-square is equal to one for two allele systems; and three for three allele systems; and six for four allele systems. The results are rounded (four decimals).
Example:
In a population was fund the following number of the three genotypes (obs),
and there is calculated the gene frequencies for the alleles A and B
and the corresponding expected (exp) under Hardy-Weinberg equilibrium.
---------
Genotype AA AB BB Total
Number, obs 36 47 23 = 106 = N
Frequency, exp p2 2pq q2 = 1,00
Number, exp 33,4 52,2 20,4 = 106
Deviation 2,6 -5.2 2,6
Chi-square 0.20 0,52 0,33 = 1,05
----------
Frequency of A is calculated as p = (2*36 + 47)/(2*106) = 0,561
do B do q = (2*23 + 47)/(2*106) = 0,439
-----
1.00
Try to put the observed numbers in the green fields of the applet and press the Calculation button.
Questions:
Calculate the gene frequency in the genetic system shown below
and a Chi-square test for H-W equilibrium.
Genotype Observed number AA 31 AB 51 BB 23 CA 55 CB 71 CC 83
Is there statistically significant deviation from H-W equilibrium ?
In the Danish Landrace are found four hæmopexin alleles with codominat inheritance. In 1969 were typed 716 animals and the results of hæmopexin type are shown below:
Hæmopexin type Number 0/0 2 0/1 16 1/1 75 0/2 10 l/2 67 2/2 20 0/3 21 1/3 229 2/3 116 3/3 160
In all cells with initial values you can put data (green fields), leave the zeros in the empty fields
The number of degrees of freedom for the Chi-square is equal to 1, 4 and 2 for the three possible combinations 2 by 2, 3 by 3 or 2 by 3 table.
Run problems
- Put your observed numbers, click the Calculate button.
Examples:
Use the applet to the test for genetic disequilibrium between two loci
A and B. The number of observed gametes is as follows:
AB gametes 10 Ab gametes 20 aB gametes 20 ab gametes 10
The numbers are given in the initial values of the applet. Factor 1 is corresponding
to locus A and Factor 2 is corresponding to locus B. Press the
Calculate button to see the result.
The Chi-square are equal to 6.66 (df=1) which is
larger then 3.84, this means that there is less than 5% chance that the genes at the
two loci segregate independently.
Questions:
Calculate a Chi-square test for the association shown below.
Genotype Observed numbers
Diseased Healthy
AA 15 27
Aa 16 28
aa 51 49
Is there statistically significant association between genotype and disease frequency ?
The two dominant genotypes can be merged into one with the following results:
Genotype Observed numbers
Diseased Healthy
A- 31 55
aa 51 49
What can justify to merge the to classes into one? Is there now statistically significant association between genotype and disease frequency ?
In a two gene system you have the following set of observed numbers:
Genotype BB Bb bb
----------------------------
AA | 57 140 101
Aa | 39 224 226
aa | 3 54 156
Are there statistically significant association between the segregating
genes at the to loci ?
In case there is found association, what does this mean ?
Can you propose a chi-square test which give 6 degrees of freedom
to test a hypothesis of linkage between the genes A and B ?
In the green field put the gene frequency for the dominant gene
- and click the Calculate button.
Examples:
If a recessive disease gene occur with a frequency of .005, 99 percent of the
diseases would be in families where both parents are normal healthy individuals.
Questions:
Which mating type produce the highest number of heterozygotic offspring when the
gene frequency p = .8 or .4 in a random mating population.
- Put your observed gamete frequencies or click the initiate Mendel
button. If the mothers gamete frequencies sum to zero, the frequencies
for the fathers is also applied for the mothers.
- Click on Next generation button calculate the gamete and genotype
frequencies in next generation.
run the applet.
In all cells with initial values you can put data (green fields) and to get the results press the Next generation button. Table values are rounded to six decimals.
Example:
When you look at segregation of genes at two loci the gametes that can
be formed are shown below and symbols are given for the observed and expected
frequencies, the deviation between the two has the symbol D for disequlibrium.
Gamete Observed frequency Expected frequency Deviation -------------------------------------------------------------- AB r p(A)*p(B) D Ab s p(A)*q(b) -D aB t q(a)*p(B) -D ab u q(a)*q(b) D
The disequilibrium gets the symbol D can be calculated from the table above, and can also be calculated as the half of the difference in the frequency of double heterozygotes in linkage- and repulsion phase:
D = r*u - t*s (= [f(AB/ab) - f(Ab/aB)]/2) from the table above
The maximum disequilibrium occurs, when all double heterozygotes are in
linkage phase f(AB/ab) or in repulsion phase f(Ab/aB). See the Figure below.

Are the recombination frequency c would D be reduced to D*(1-c) per generation, and for the n'th generation Dn = D0*(1-c)n.
If you apply the initial values r=0.1, s=0.2, t=0.3, u=0.4 and press the Next generation button, you will see calculated all the genotype frequencies and D=0.0199 rounded 0.02. If you continue using the Next generation button more times with c=0.5 you will see that D= approach 0 which means observed and expected gamete frequencies are equal i.e. r=0,12.
Questions:
Calculate the gamete frequency in the first 5 generations
and the equilibrium gamete frequencies in the genetic system shown below
where the recombination frequencies between the two loci A and B is c=0.2.
Gamete Observed frequency AB 0.21 Ab 0.49 aB 0.19 ab 0.11
What would be the frequencies of the two types of double heterozygotes
in next generation?
How many generations will it take to reach equilibrium within 0.02 units ?
Repeat the calculations for c=0.05.
In a F3 after a cross between two pure lines aabb X AABB. What would
be the gamete frequencies if c=.5 , .4 and .1 ?
Hints: Use the initiate mendel button and use the next generation button more times.
In all cells with initial values you can put data (green and/or
yellow fields)
You can put either real observations (numbers) or relative genotype
frequencies in the green fields.
you see this text you can't run this applets chose Options | Network
Click the Calculate button.
Put the fitness of the genotypes (relative or numbers) and
you can run one generation at the time by pressing the button +1 generation!,
or you can get a graph over gene frequency changes over 60 generations by pressing
the Run button. The corresponding data you can extract over the clip board in the
lower left window.
You can also start the process by putting your gene frequencies and
there after take some selections rounds.
For practical reasons delta q is put to 0 for values less than .000001.
Sometimes when delta q is less than .0001 there are problems with rounding
and some browsers can not see the results proper.
Example:
If you have a genetic system for instance yellow coat colour in the Labrador Retriever, where the recessive (yellow) have the fitness 1-s by selection you get:
Genotype EE Ee ee Total ---------------------------------------------------------------- Observed number 141 80 11 = 232 Frequency p2 2pq q2 = 1.00 Fitness 1 1 1-s Proportion p2 2pq q2(1-s) = 1-sq2 after selection ---------After selection the gene frequency q' can be calculated by the gene counting method, q' is the gene frequency in the next generation, is calculated as half of the heteroygotes plus the surviving recessive relative to half of the proportion of all surviving genes, that is equal 1-sq2.
q' = (2pq/2 + q2(1-s))/(1-sq2)To test the applet put the observed number and press the Calculate button. You then get q=0.2198, if you have s(aa)=0 and press the +1 generation button you get q'=0.1802.
Questions:
Calculate the gene frequency in the first 5 generations
of selection and the equilibrium gene frequency in the genetic system shown below
with selection favouring the heterozygotes with s1 = 0.3 and s2 = 0.5
Genotype AA Aa aa Total Observed numbers 225 157 43 Frequency p2 2pq q2 = 1,00 Fitness 1-s1 1 1-s2 Proportion p2(1-s1) 2pq q2(1-s2) = 1-p2s1 - q2s2 after selection
How many generations will it take to reach equilibrium within 0.02 units ?
What would happen after 5 generations selection if s1 = -0.3 and s2 = -0.5
Would there be any equilibrium ?
In all cells with initial values you can put data (green and/or
yellow fields)
You can put either real observations (numbers) or relative genotype
frequencies in the green fields.
you see this text you can't run this applets chose Options | Network
Click the Calculate button.
Put the fitness of the genotypes (relative or numbers) and
you can run one generation at the time by pressing the button +1 generation!,
or you can get a graph over gene frequency changes over 60 generations by pressing
the Run button. The corresponding data you can extract over the clip board in the
lower left window.
If you define population size (pop. size) you can simulate random changes in
gene frequencies over time.
If you define more populations (number of pop.) you get an average estimate of the
gene frequenices over generations and its standard error.
If you use large and many populations the simulation might take several minutes, start
with few and small populations so you can have an impression of the time consumption on your
computer.
For utilization of the deterministic model the upper part of this applet go to applet 3.4 and its explanation.
Example:
If you have a genetic system (Aa) with gene frequency q=.5. and you have random mating. How many populations out of ten would either have lost or fixed the gene a after 20 generations ? after 40 ? and after 60 generations ?
Put 10 in the pop size box, and pres Run 10 times recording loss or fixation of gene 'a' in each run.
Questions:
Calculate the gene frequency in the first 60 generations
of selection in the genetic system shown below
with selection favouring the heterozygotes with s1 = 0.3 and s2 = 0.5
having a population size of 20.
Genotype AA Aa aa Total Observed numbers 225 157 43 Frequency p2 2pq q2 = 1,00 Fitness 1-s1 1 1-s2 Proportion p2(1-s1) 2pq q2(1-s2) = 1-p2s1 - q2s2 after selection
Will equilibrium within 0.02 units be reached ?
Matrices are just defined by line length and number of lines. To edit data in the data field is very troublesome as the return key can not be used for giving a new line as it works as pressing the eval. button. For larger sets of data use notepad or any other editor. Move the data to the input area by means of the clip board using ctrl-ins (copy) and shift-ins (insert).
Example:
Example of calculating inbreeding where the columns in the matrix shown below
are animal, sire
and dam, where the oldest animals should appear first. The pedigree are
converted in the 'a' matrix as done below (0 means unknown parent):
animal sire dam --------------- a = 1 0 0 2 1 0 3 1 0 4 1 0 5 2 3 6 4 3 7 5 6 |
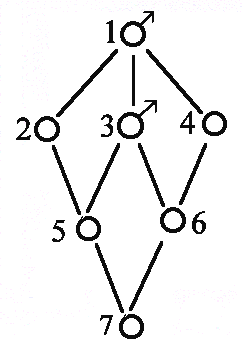
|
Take these data including (a=) in the clip board and transfer them to input window
and there after press the 'evaluate' button and the matrix should appear
in the result window.
There after use in the input window:
rel = :tabular(a)and press the 'evaluate' button
The rel relationship matrix will appear in the result window and will look as shown below. Number of digits can be set, replacing the 6 with 3 will change the number of digits to 3.
Relationship matrix 1+F (inbreeding) in the diagonal
rel =
1.000 0.500 0.500 0.500 0.500 0.500 0.500
0.500 1.000 0.250 0.250 0.625 0.250 0.437
0.500 0.250 1.000 0.250 0.625 0.625 0.625
0.500 0.250 0.250 1.000 0.250 0.625 0.437
0.500 0.625 0.625 0.250 1.125 0.437 0.781
0.500 0.250 0.625 0.625 0.437 1.125 0.781
0.500 0.437 0.625 0.437 0.781 0.781 1.218
The inbreeding for each animal is given by its diagonal element minus
one, i.e. the last three animals are inbred with an inbreeding coefficient
of 0.125, 0.125 and 0.218 respectively.
If you are interested in the inbreeding coefficient, only, you run the inbred procedure as follow:
inb = :inbred(a)
you will have the following, in the results window, with animal number and inbreeding coefficient:
Animal F (inbreeding)
inb =
1.000 0.000
2.000 0.000
3.000 0.000
4.000 0.000
5.000 0.125
6.000 0.125
7.000 0.218
For inverting the relationship matrix use the command:
inv = :invert(rel)
Or setting up the inverse relationship matrix direct from the a matrix only to use with non inbreeding:
d_inv = :dinvers(a)Which put the inverse relationship matrix in the output window
Below is shown a hand calculated example with the two general formula
in use.
The relationship between two animals is the average relationship between
the oldest and the others two parents.
and the inbreeding of an individual is half the relationship between
the two parents.
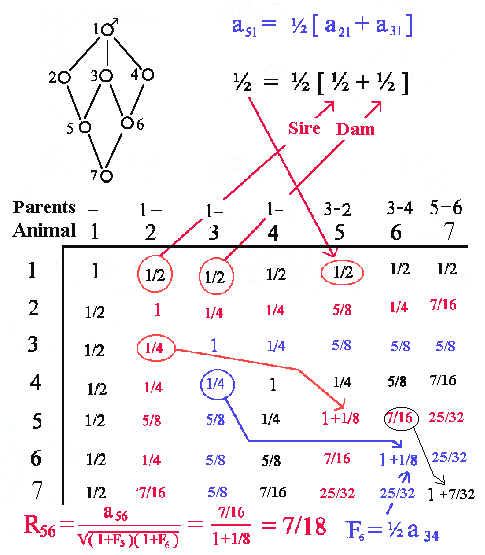
For your own data put them in the matrix 'a' and repeat the process:
Questions:
In the pedigree shown below the individuals have been assigned the numbers
from 1 to 11.
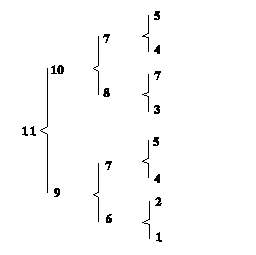
|
Animal Sire Dam , where 0 means unknown
1 0 0
2 0 0
3 0 0
4 0 0
5 0 0
6 2 1
7 5 4
8 7 3
9 7 6
10 7 8
11 10 9
|
Calculate the inbreeding coefficient for the individuals No 10 and 11, and calculate the additive relationship coefficient between individual 11 and all others in the pedigree. The data set to be used for the calculations is given above.
What would be the inbreeding coefficient after 5 generation of full sib mating?
Example:
Test of segregation ratios from known mating can be done by Chi-square
test. If you have a test mating between two heterozygotes Aa x Aa the offspring
would have an expected segregation ratio of 1:2:1 as shown in the table below, where
the ratios are converted to a 0.25 : 0.5 : 0.25.
Genotype AA Aa aa Total ----------------------------------------------------------------- Number, obs 30 51 39 = 120 = N Frequency, .25 .5 .25 = 1,00 Number, 30 60 30 = 120 Deviations 0 -9 9 Chi-Square 0 1,35 2,70 = 4,05 ----------To test the applet put the bold face values from the table in the applet and press the Calculate button.
The number of degrees of freedom is df = 3-1 = 2, as the material is only providing the parameter N being used to calculate the expected numbers. The Chi-square value is less than the test value 5,99, which means that there is not statistically significant deviations from a 1:2:1 segregation ratio on the 5% level.
Questions:
Calculate a Chi-square for the following observation set from test
mating of known carriers.
Total numbers of observations 30 Number of affected 16
Is the segregation ratio statistically significant different from a 1:3 segregation ratio ?
In the cells with green colour put your data and press the Calculate button.
Example:
The disease tyrosinemia in mink is investigated by the following set
of field data for recessive Mendelian inheritance. A description of the
disease tyrosinemia in mink are published by Christensen et al. Canadian
J. Comparative Medicine, 43:333-340, 1979.
In the data set 16 litters are included with at least one affected offspring. The observed numbers are given below.
T = 94 - total numbers of pups A = 32 - total number of affected A1 = 4 - number of families with one affected pup A2 = 9 - number of families with two affected pupsThe applied formulas for test of Mendelian inheritance by "Singles method" (with the proportion p-hat ) are shown in the figure below. The tyrosinemia data are applied to show the use of the formulas.
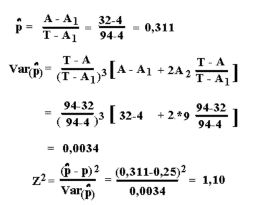
The Z2 are Chi-squared distributed with 1 degree of freedom. The test of p-hat is against 0,25, this is the expected ratio when both parents are carrier and there is recessive inheritance. The test value is less than 3.84. Therefore the deviations can be accepted as not statistically significant.
Questions:
Calculate the corrected segregation ratio for the following observation set of field
data, where there has been at least one affected per family.
T = 30 - total numbers of observations A = 16 - total number of affected A1 = 12 - number of families with one affected A2 = 2 - number of families with two affected
Is the segregation ratio statistically significant different from 1:3 segregation.
Applet for mean, Genotypic and Breeding values and Dominance
In all cells with initial values you can put data (green and/or yellow fields)
Run problems
Example:
All the values are calculated by the classical formula for a mean value and
the breeding value is defined as shown below. To see the results
press the Calculate button.
Questions:
Compare the results, for which gene frequency are there the smallest
difference in breeding value between the three genotypes and the smallest
additive variance? why ?
The halothane locus (Hal) has influence on the quality of
swine meat on the basis of a meat quality index where meat colour
is the main component. The average index for the (Hal) genotypes
are given below:
In all cells with initial values you can put data (green fields) and
press the Calculate button. Results are rounded to four decimals.
Example:
Questions:
Compare the results, which animal have the highest breeding value for
each heritability? And which one have the most accurate estimate for each heritability ?
The applet can handle inbreeding, relationship, calculating the inverse
and estimating animal model breeding values. It will perform well up to 2000 observations and might be even more.
It has been made for solving smaller scientific problems and for educational purposes. It is worth to note that the numeration
of the animals is free as long as the oldest appear first.
code=TabularApp.class
name=TabularApp
width=800
height=500 >If
you see this you can't run the applet.
The estimating the animal model breeding values, command an=:animalm(a), can correct for any number of class variables
or continued variables in any combinations.
The first data line specify the parameters as follows - referring to first example below as well as in general
Example of estimating animal model breeding values for 8 animals, where the input file contains:
The selection response is calculated in the lower 3 rows of the applet
according to the formula shown below. The delta G is calculated per year (år). If the generation
interval is set to one year the results is also per generation.
The parameters are
Example:
Questions:
If the males as well as the females were selected on own performance calculate delta G.
Repeat the calculations with a heritability of 0.10
Applet for calculating heritability for threshold traits.
Example:
Illustration of the case where both parents are affected are given below.
The applet is initiated with the actual data; to see
the calculations press the Calculate button.
Questions:
Estimate the heritability.
The test example is the transfferin example given in Veterinary Genetics. Jersey
cows with the genotype tt yield 2082 kg milk
and cows with the genotypes Tt and TT yield 1882 kg milk. The
gene frequencies p(T) and q(t) are given as 0,67 and 0,33, respectively.

Calculate the breeding value and dominance deviation for the gene frequencies
p equal .1, .2, .3, .4, .5, .6, .7, .8 and .9 for the following genotypic
values
A2A2 100
A1A2 115
A1A1 110
Genotype Meat-quality-index
N/N 8.00
N/n 7.10
n/n 6.00
Suppose that the frequency of q(n) = 0.20 calculate the following:
a) the average Meat-quality-index for the population,
b) the average Meat-quality-index for offspring from
individuals with the genotype
N/N respectively n/n supposing random mating in the population,
c) the breeding value of the three genotypes
d) the additive variance, due to the halothane locus,
e) the proportion of the additive varianceHal
of the total additive variance for the Meat-quality-index
as its h2 = 0,44 and varianceP =1,69.
7.2 Estimating simple forms of breeding values
The breeding value can be based on own, fathers + mothers record as well
as average of offspring or sibs to the animals. Heritability, repeatability,
common environmental effect (milieu) for full sibs and population mean
value have to be specified. In the last case relationship (a and a') shall be defined.
The relationship (a) between the related individuals giving
the phenotypic measurements; with the relationship (a') to the animal being evaluated.
The 'common milieu' is used when full sibs are measured.
can't run the applet.
If you want to see how the applet
work before you enter your own data just press the Calculate button using
the initial values.
In the figure below you see a regression line for the index (I) for
the true breeding value (A) of an individual based on measurements (average
of the records for offspring, sibs etc. = P's).. The coefficients of relationship can be defined in the
bottom line.
P'er = phenotype measurments
n = number of phenotypes
Pg bar = average of the P's
a' = relationship between the index animal and the P's
a = relationship between the P's
P bar = Populationen mean
A bar = Populations mean A's = P bar
h2 = heritability
c2 = common environmental factor for the P's
rAI = the accuracy of the index
t = a h2 + c2 = phenotypic correlation between P's

Calculate the breeding value for the following animals when Mean=100 and the
heritability have the following values 5, 10, 25, 40 and 60 %.
own performance 110
average of the parents 115
10 half sib offspring 106
100 half sibs 105
7.2 Estimating animal model breeding values
The calculations are based on
the general matrix part which has been borrowed from Bryan Lewis's General Matrix Applet.
The general part include for instance multplication as A=b*c or A=b*c' which can be used together
with the the animal model calculations.
For class variables the fist class is excluded for not having
a degree of freedom as the mean value always is calculated.
Zero is treated as missing value so if zero is a part of the observation set a constant should be added.
The first 3 columns in the dataset shall contain animal, sire and dam - all other columns can be used freely
1. 1 specify (sigmaE/sigmaA)2 which in this case equals h2 = .50
2. 0 printing the solutions
1 printing the solutions and the accuracy squared, for smaller number of data (pc-time problems)
2 printing the triangualrization inclusive dependent var - last line the solutions
3 printing the rearranged input with classes from zero to n-1 and dependent variable as the final.
4 printing the equations inclusive the dependent var.
3. 0 normal model
1 model with inbreeding - for smaller number of data (more roundings and pc-time problems)
4.- 0 exclude the trait from the analyse
1 specify a continued variable where the last one is the dependent trait
-1 specify the dependent trait if not the last trait - which is then interchanged with the last variable
2 specify a class variable
3 specify a class variable but with all classes included (this can not be solved)
Animal Sire Dam, where 0 means unknown, one fixed factor, two continued vars. and the trait litter size
- except first line which specify the parameters explained above.
Put the data below in the input window
followed by a return stroke
a=
1 0 0 2 1 1 1
1 0 0 3 2 0 10
2 0 0 2 3 1 9
3 0 0 1 4 0 8
4 0 0 2 1 1 7
5 1 2 1 5 1 9
6 1 2 1 6 0 10
7 3 4 2 4 1 8
8 5 6 3 6 1 11
Genealogical diagram
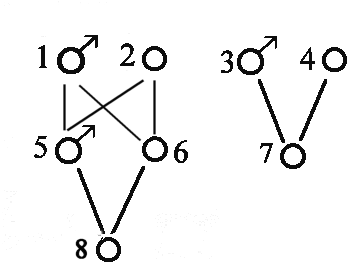
Resulting in the following
in the output window
a =
1 0 0 2 1 1 1
1 0 0 3 2 0 10
2 0 0 2 3 1 9
3 0 0 1 4 0 8
4 0 0 2 1 1 7
5 1 2 1 5 1 9
6 1 2 1 6 0 10
7 3 4 2 4 1 8
8 5 6 3 6 1 11
Followev by an=:animalm(a)
and a return stroke resulting in
Animal model solutions
an =
1.0000 0.1955
2.0000 0.4287
3.0000 -0.3799
4.0000 -0.2443
5.0000 0.3420
6.0000 0.3582
7.0000 -0.4206
8.0000 0.2903
0.0000 6.9749 mean value
2.0000 0.5183 class there is no degree of freedom for class 1
3.0000 1.8716 class
0.0000 0.4191 regression 1
0.0000 -0.5322 regression 2
In the referred theory by Poul Jensen the first example on growth rate in young pigs can not be solved as the class year is given for all animals as follows.
But the system will nullify the first year and it is then converted to a regression giving 4.3883 gram extra the second year.
The heritability is set to 0.33.
a=
2 0 0 2 1
1 0 0 0 0
2 0 0 1 225
3 0 0 1 220
4 0 0 1 255
5 1 3 2 250
6 1 3 2 198
7 2 4 2 245
8 2 4 2 260
9 2 4 2 235
Genealogical diagram
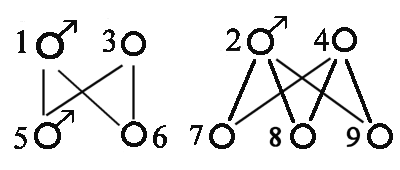
Animal model solutions
animal estimate
an =
1.0000 -3.1844
2.0000 -0.3009
3.0000 -6.2135
4.0000 9.6990
5.0000 -1.0912
6.0000 -11.4912
7.0000 5.4271
8.0000 8.4271
9.0000 3.4271
0.0000 232.2718
0.0000 4.3883
In case some of the parents are inbred the estimates will not be the same. In the following
small example solutions are made with (parameter 3 set to 1) and without inbreeding. Example 2.1 from RA Mrode
'linear models for estimating breeding values, CABI Publishing'.
The heritability is set to 0.33.
a=
2 0 1 1
1 0 0 15
2 0 0 19
3 1 2 7
4 1 0 13
5 4 3 22
6 5 2 10
Genealogical diagram
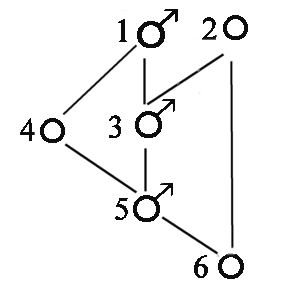
Animal model solutions
not accounting for inbreeding
an =
1.0000 -0.3699
2.0000 0.1725
3.0000 -1.0988
4.0000 0.1110
5.0000 0.7084
6.0000 -0.5484
0.0000 14.5041
Animal model solutions
accounting for inbreeding
an =
1.0000 -0.3665
2.0000 0.1689
3.0000 -1.0983
4.0000 0.1131
5.0000 0.7070
6.0000 -0.4987
0.0000 14.4957
Estimating of the accuracy squared for the estimate; example 3.1 RA Mrode.
The heritability is set to 0.33.
a=
2 1 0 2 1
1 0 0 0 0
2 0 0 0 0
3 0 0 0 0
4 1 0 1 4.5
5 3 2 2 2.9
6 1 2 2 3.9
7 4 5 1 3.5
8 3 6 1 5.0
Genealogical diagram
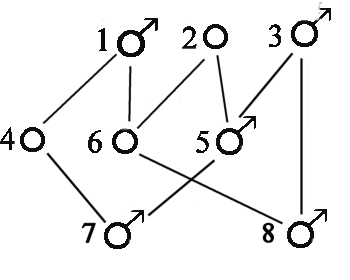
Animal model solutions
with its squared accuracy
an =
1.0000 0.0984 0.0578
2.0000 -0.0187 0.0158
3.0000 -0.0410 0.0870
4.0000 -0.0086 0.1446
5.0000 -0.1857 0.1437
6.0000 0.1768 0.1154
7.0000 -0.2494 0.1162
8.0000 0.1826 0.1552
0.0000 4.3585 0.0000
0.0000 -0.9540 0.0000
Larger example solutions for y, note that there is free numbering of the animals as long as the oldest occur first,
sex 2 has a 5.6002 uits lower performance.
which have been produced by late Poul Jensen.
animal sire dam y sex trait2
a=
2 0 0 -1 1 2
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
7 0 0 93 2 2
8 1 2 78 1 2
9 1 2 63 1 3
10 1 3 91 1 3
11 1 3 70 2 3
12 1 3 100 2 2
13 1 4 102 1 4
14 1 5 119 1 5
15 1 5 121 2 4
16 1 6 93 2 6
17 1 6 81 2 4
18 1 6 82 2 3
19 14 17 78 2 2
20 14 17 88 1 5
21 14 17 85 2 6
22 14 7 91 2 5
23 14 7 113 1 7
24 14 7 118 2 5
25 14 15 91 2 4
26 14 15 83 2 2
27 14 15 102 1 4
128 14 12 87 2 5
29 14 12 83 1 3
30 14 12 86 1 3
31 14 16 106 2 4
32 14 16 90 1 5
33 14 16 57 2 3
34 23 25 82 1 2
35 23 25 84 1 1
36 23 25 77 2 3
37 23 22 83 2 2
38 23 128 95 1 5
39 23 128 68 2 4
40 23 31 116 1 6
41 23 31 112 1 7
42 23 31 88 2 5
43 23 24 121 1 4
44 23 24 98 1 4
45 23 24 86 1 4
Animal model solutions
The first variable contains numbers
of animal (mean) classes and regressions
and the second the estimate
an =
1.0000 -1.4325
2.0000 -4.4927
3.0000 3.1002
4.0000 0.4142
5.0000 2.9162
6.0000 -3.3706
7.0000 2.8651
8.0000 -4.7612
9.0000 -5.6569
10.0000 2.9802
11.0000 -0.0996
12.0000 2.7212
13.0000 -0.0949
14.0000 -0.4850
15.0000 4.8850
16.0000 -3.7721
17.0000 -6.5152
18.0000 -0.2880
19.0000 -4.0711
20.0000 -5.4854
21.0000 -5.5097
22.0000 -0.0535
23.0000 -1.6506
24.0000 5.2497
25.0000 0.6864
26.0000 1.4889
27.0000 2.0724
128.0000 -3.1481
29.0000 1.6076
30.0000 2.2076
31.0000 0.8187
32.0000 -3.9882
33.0000 -5.0696
34.0000 -1.9767
35.0000 -0.4821
36.0000 0.2475
37.0000 -0.9527
38.0000 -3.2048
39.0000 -7.2870
40.0000 2.0375
41.0000 -0.6642
42.0000 -1.8980
43.0000 5.5520
44.0000 0.9520
45.0000 -1.4479
0.0000 90.0823
2.0000 5.4732
3.0000 -5.0481
4.0000 15.9558
5.0000 16.9446
6.0000 19.6661
7.0000 29.1753
0.0000 -5.6002
8.2 Estimating breeding values and selection response
The breeding value can be based on any uniformly related individuals
to the animals or own record, see applet 7.2,
remember the actual relationships a and a' should be
properly defined. By pressing the Calculate button the accuracy is transferred to the
delta G input window.
can't run the applet.
In all green fields you should define values
then press the Calculate button. The delta G can be run independently
of the breeding value estimations, all values in the yellow fields shall be defined.
Selection intensity, i
Accuracy of selection, rAI
Generation interval, L
The additive standard deviation, sigmaA
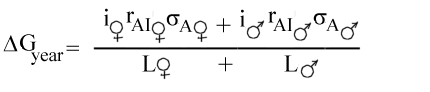
The accuracy is automatically transferred from the breeding value estimation, but you
can also convert an externally derived accuracy squared
by means of r2 to r button. If you have the proportion
selected (p) put your data in the (i) field and press the convert p to
i button.
The calculation is based on the average of the contribution from the
sires and dams. With the given initial parameters delta G is 0.04 units if you press
the Calculate delta G button.
In a population are selected 10 % males based on progeny test of 20 offspring
and 50 % females based on own performance. SigmaA is set to 1.
Calculate delta G per generation when the heritability is 0.40.
Compare the two results
8.3
Applet for calculating heritability for threshold traits (diseases)
The calculations are based on disease frequencies in the general population (Population) and
among relatives (Indiv. related ) to diseased animals. The relatives can be
(both parents diseased) first degree (father, mother or full sibs) or second
degree (half sibs, grand parents).
Observe: The chi-square test calculation is based on: that the related ones is subtracted from the population numbers!
Enter your observed numbers and degree of relationship (green
fields) and then press the Calculate button. The values in the (Degree of relationship) field should 1, .5 and .25 for the
three above mentioned cases.
You can also enter the frequencies (yellow fields) but then the numbers shall be zeros
in the observed number fields. Results are rounded to four decimals.

In the table below is given observed numbers for disease frequencies in the
population and in first-degree relatives to diseased animals.
Normal Diseased Frequency
------------------------------------------
Population 980 20 0.020
First-degree
relative 140 10 0.066
------------------------------------------
What is the relative risk to be related to a diseased animal ?
Is the heritability statistically significant different from 0 with (p< 0.05) ?